§ 3. Предел числовой последовательности. Предел функции.

Ч исло называется пределом последовательности , если для любого существует натуральное число такое, что при .

В случае, если последовательность имеет своим пределом число , говорят также, что последовательность сходится (или стремится) к числу , и обозначают этот факт так: .

Если последовательность не имеет предела, то говорят, что она расходится.

Пример 6.14. Используя определение предела, докажите, что последовательность сходится к числу 2.

О бозначив , выберем произвольное число . Тогда и неравенство будет выполнено тогда, когда , т.е. . Положив (где означает целую часть ), получим, что для всех справедливо неравенство . В соответствии с определением предела это и означает, что .

Ч исло называется пределом функции в точке , если для любого существует такое, что при выполняется неравенство . Это кратко записывается в виде .

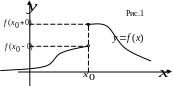
Если есть предел в точке , то на графике это иллюстрируется следующим образом. Так как из неравенства следует неравенство , то это значит, что для всех , отстоящих от не далее чем , точка графика функции лежит внутри полосы шириной , ограниченной прямыми и . Очевидно, что с уменьшением величина также уменьшается.

Односторонние пределы

П редел называется пределом слева данной функции в точке .

П редел называется пределом справа данной функции.

Ч исло A называется пределом функции в точке , если для любого существует число , что при всех выполняется неравенство .

Ф ункция называется ограниченной в области , если существует постоянное число такое, что для всех .

Пример 6.15. функция ограничена для всех , так как в этой области .

§ 4. Теоремы о пределах.

1. Предел суммы конечного числа функций равен сумме пределов этих функций, т.е.

2. Предел произведения конечного числа функций равен произведению их пределов, т.е.

С ледствие. Если , то .

3. Предел частного равен частному пределов

,

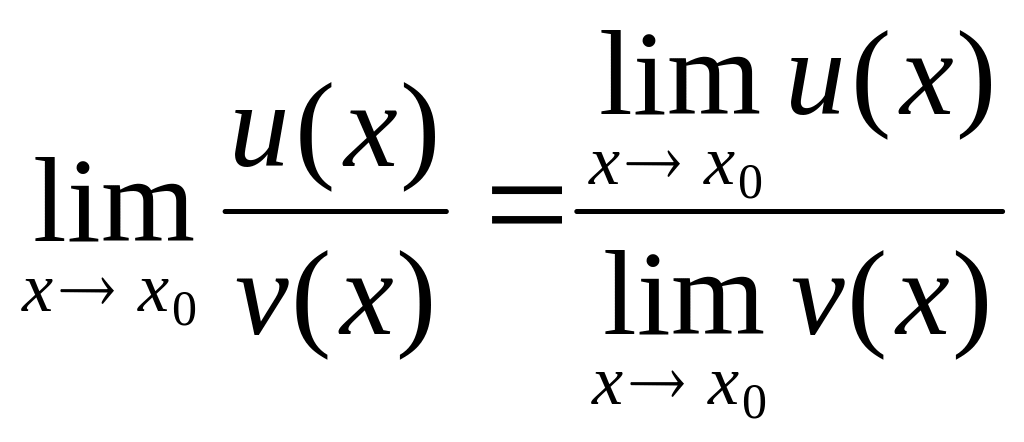если предел знаменателя не равен нулю .

Пример 6.16. Используя теоремы о пределах, найдите

.

.

Пример 6.17. Используя теоремы о пределах, найдите

.

. Имеем неопределённость. «Раскроем» эту неопределённость (т.е. избавимся от неё), разложив числитель и знаменатель на множители и сократив их далее на общий множитель :

.

Пример 6.18. Используя теоремы о пределах, найдите

.

. Имеем неопределённость. Домножим числитель и знаменатель дроби на выражение, сопряжённое к числителю:

.

З амечательные пределы

(6.1)

, (6.2)

где — иррациональное число, .

Пример 6.19. Найдите .

. Имеем неопределённость. Поделим числитель и знаменатель дроби под знаком предела на и воспользуемся первым замечательным пределом (формула (6.1)):

.

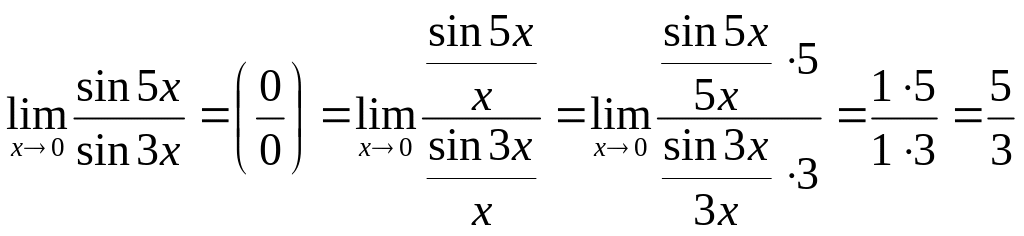Пример 6.20. В п.3 §2 была приведена формула вычисления конечной величины начальной суммы через лет в случае, если удельная процентная ставка есть , а проценты начисляются раз в году. Вычислим сумму , если начисление процентов происходит непрерывно, т.е. .

=

=

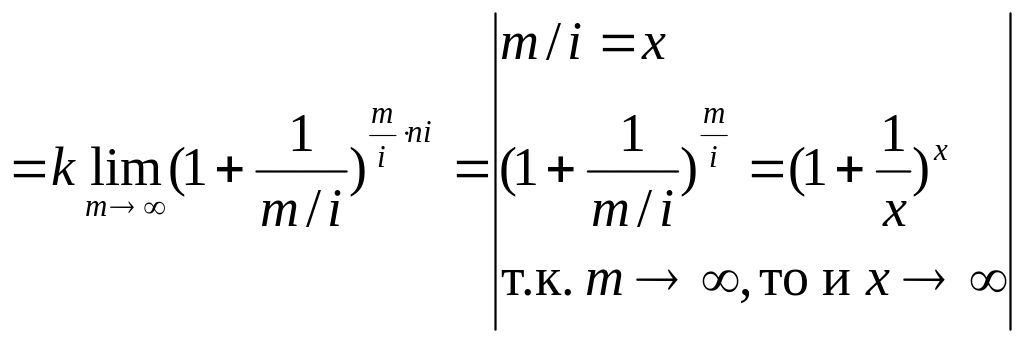(в силу (6.2)) = .