Физикохимия металлургических систем и процессов. Щетинин А.А., Сушко Т.И

УДК 621.74

Щетинин А.А. Физикохимия металлургических систем и процессов: учеб. пособие [Электронный ресурс]. – Электрон. текстовые и граф. данные (1,5 Мб) / А.А. Щетинин, Т.И. Сушко. - Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2016. – 1 электрон. опт. диск (DVDROM) : цв. – Систем. требования : ПК 500 и выше ; 256 Мб ОЗУ ; Windows XP ; SVGA с разрешением 1024x768 ; Adobe Acrobat ; CD-ROM дисковод ; мышь. – Загл. с экрана.

В учебном пособии излагаются закономерности пирометаллургических процессов, т.е. совокупности операций по получению металлов и сплавов, протекающих при высоких температурах и осуществляющихся в различных печах и плавильных агрегатах. Рассматриваются физические и химические процессы, происходящие при получении различных металлических

(направленность «Технология литейных процессов»), дисциплине «Теория металлургических процессов». Предназначено для студентов третьего курса.

Табл. 16. Ил. 57. Библиогр.: 17 назв.

Рецензенты: ООО «Автолитмаш» (начальник производства С.Б. Воронин); д-р техн. наук, проф. В.А. Небольсин

©Щетинин А.А., Сушко Т.И., 2016

©Оформление. ФГБОУ ВО

«Воронежский государственный технический университет», 2016

ВВЕДЕНИЕ

Литейное производство как наука и как отрасль промышленности находится между металлургией и машиностроением. Для того чтобы получить годную для использования деталь машины или какого-либо устройства, нужно не только обеспечить её точную форму, но и структуру металла, её эксплуатационные свойства. Эти задачи решаются на стадии подготовки металлических материалов, заливаемых в литейную форму. Они непосредственно связаны с теми проблемами, которые решает металлургия.

Становление металлургии как науки относится к концу 19 – началу 20 века и связано с открытием Д.И. Менделеевым Периодического закона, развитием представлений о строении атома, открытием законов физико-химического

металлургических процессов. Наибольший вклад в развитие металлургии внесли отечественные ученые – П.П. Аносов, Г.И. Гесс, Д.К. Чернов, Н.Н. Бекетов, Н.С. Курнаков, А.А. Байков, И.П. Бардин, Н.Н. Семенов, Д.А. Франк – Каменецкий, И.А. Соколов, М.А. Павлов, В.В. ГрумГржимайло, П.В. Гельд и многие другие. Среди зарубежных ученых следует отметить работы Гиббса, Вагнера, Шенка,

операций по получению металлов и сплавов, протекающих при высоких температурах и осуществляющихся в различных печах и плавильных агрегатах. Рассматриваются физические и химические процессы, происходящие при получении

свойствами, подготовке сплавов к использованию в литейных технологиях. К ним относятся процессы горения газообразного и твердого топлива, образование и распад химических соединений, окисление и восстановление металлов, взаимодействие газовой, жидкой и твердой фаз, процессы массо- и теплопереноса.

Для специалиста, работающего в области литейного производства, важно понимать, уметь описывать и предсказывать такие процессы как на макроскопическом, феноменологическом уровне, так и на микроскопическом уровне, на языке атомно-молекулярной теории.

Основными «инструментами» исследования металлургических процессов являются методы химической термодинамики и химической кинетики. Эти методы кратко рассмотрены в первой главе данного учебного пособия. В последующих главах учебный материал располагается в порядке усложнения рассматриваемых металлургических систем. Вначале рассматриваются процессы в газофазных системах, затем процессы взаимодействия газов и твердых тел, топохимические реакции, процессы взаимодействия между конденсированными фазами. Каждая металлургическая система характеризуется термохимически, кинетически и, по возможности, - описываются механизмы протекающих в данных системах процессов.

4

1. МЕТОДЫ ФИЗИКО-ХИМИЧЕСКОГО ОПИСАНИЯ МЕТАЛЛУРГИЧЕСКИХ ПРОЦЕССОВ

1.1. Основные понятия термодинамики

При получении металлов и сплавов, а также при изготовлении изделий из них методами литья протекают различные физические и химические процессы: горение газов и твердых горючих материалов, образование химических соединений из простых веществ, распад химических соединений, диффузия атомов и молекул в газах, жидкостях и твердых телах и многие другие. Для того, чтобы получать материалы и изделия с заданными свойствами, надо уметь предсказывать и описывать такие процессы как на макроскопическом уровне – в системах, состоящих из большого числа частиц, так и на атомно-молекулярном уровне – при взаимодействии двух или нескольких частиц.

Всякая совокупность тел, которая фактически или мысленно может быть выделена из окружающей среды, называется системой (или термодинамической системой). Система называется изолированной, если она не обменивается веществом или энергией с окружающей средой и ее объем постоянен.

Система, не обменивающаяся веществом с окружающей средой, называется закрытой, в противном случае она называется открытой.

Процессы, изучаемые в курсе ФХМСП, описываются на основе законов химической термодинамики и химической кинетики, которые являются важнейшими разделами физической химии.

Химическая термодинамика отвечает на три вопроса:

1.Возможен ли данный процесс в системе при определенных (заданных) условиях?

2.В какую сторону пойдет самопроизвольный процесс при указанных условиях?

5

3. Чем этот процесс закончится (т.е. каким будет состояние равновесия)?

При этом термодинамика не рассматривает вопрос о скорости процесса (время вообще не фигурирует в законах термодинамики) и его конкретном механизме. Эти вопросы являются предметом химической кинетики, которая позволяет найти из опыта или оценить теоретически скорость процесса, она рассматривает также конкретные атомномолекулярные механизмы (модели) процесса.

Вещества могут находиться в разных агрегатных состояниях. Например, хорошо известны агрегатные состояния Н2О: вода, лед, пар. При определенных условиях могут одновременно сосуществовать разные агрегатные состояния вещества. В таких случаях говорят о фазовых равновесиях.

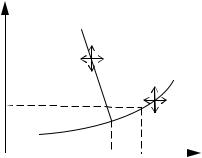
Фазовые равновесия удобно изображать графически в виде фазовых диаграмм. На рис. 1.1 показан пример такой диаграммы для однокомпонентной системы без полиморфных (аллотропических) превращений в твердом состоянии.

Р

В

однокомпонентной системе можно задавать лишь один параметр. Например, если задать температуру Т, то из условия равновесия можно найти давление насыщенного пара

Р1 .

В точке О ( Ро , То ) одновременно существуют три фазы; эта точка называется тройной. Для сохранения равновесия между тремя фазами нельзя изменять ни давление, ни температуру. На линиях равновесия для его сохранения мы можем согласованно менять внешние условия ( Р и Т). внутри каждой однофазной области можно произвольно менять давление и температуру.

Если при изменении параметров системы происходит переход через границы фазового равновесия, то совершается процесс, называемый фазовым превращением. Фазовые превращения обычно осуществляют изменением одного параметра, тогда как другой фиксируется (показано стрелками). Точка К - критическая точка. Выше этой точки различия между газом и жидкостью исчезают.

Вспомним некоторые определения параметров многофазной системы.

Фазой называется некоторая часть неоднородной системы, представляющая собой совокупность материальных объектов, имеющих определенный химический состав и термодинамические свойства, отделенная от других частей системы поверхностью раздела. Фаза может быть, в принципе, извлечена из системы каким-либо механическим способом.

Числом степеней свободы называется число независимых параметров, задание которых полностью определяет состояние системы при равновесии и значения которых можно произвольно менять в известных пределах, сохраняя число и природу фаз, находящихся в равновесии. Для однокомпонентной системы параметрами состояния являются давление и температура. Для многокомпонентных систем параметрами являются также концентрации всех

7

компонентов в каждой фазе. Числом компонентов (к), называется число индивидуальных веществ, из которых состоит система, за вычетом числа независимых химических уравнений, связывающих эти вещества. Например, в системе, состоящей из СО, СО2, О2, Fe и FeO число индивидуальных веществ равно 5. Они связаны между собой химическими уравнениями:

1)2 Fe + О2 = 2 FeO;

2)FeO + СО = Fe + СО2;

3)2СО + О2 = 2СО2.

Однако независимых уравнений всего 2, т.к. третье уравнение (3) получается суммированием (1) и (2) (последнее предварительно нужно умножить на 2). Таким образом, число

между числом компонентов (к), числом фаз, существующих при равновесии (φ ) и числом степеней свободы системы ( i )

Например, для однокомпонентной системы максимальное число фаз равно 3 (тройная точка). Часто приходится иметь дело с процессами, происходящими при заданном и постоянном внешнем давлении. Так как термодинамические параметры конденсированной фазы слабо зависят от давления, то на практике – это любые процессы, протекающие в твердой или жидкой фазах при умеренных давлениях. При постоянном давлении остается только один

Из этого уравнения следует, что при заданном давлении (например, атмосферном) плавление твердого однокомпонентного тела может происходить только при постоянной температуре. Действительно, температура плавления – это температура, при которой в равновесии находятся жидкая и твердая фазы. Тогда i = 1 + 1 – 2 = 0 – т.е. при равновесии температура не может изменяться, а при изменении температуры одна из фаз должна исчезнуть. Если i = 0, систему называют нонвариантной, i = 1 – моновариантной, i = 2 – дивариантной и т.д.

Важное значение для анализа различных физикохимических процессов имеет принцип Ле-Шателье.

Если на систему, находящуюся в равновесии оказать какое-либо воздействие, то в результате протекающих в ней процессов равновесие сместится в таком направлении, что оказанное внешнее воздействие уменьшится.

Например, равновесие реакции 2 NО + О2 2 NO2 при увеличении давления сместится вправо, т.к. в результате ее протекания уменьшается число частиц в системе (и ее объем) и понижается давление.

При помощи термодинамики, базирующейся на опытных законах (началах), можно находить энергетические эффекты различных превращений, а также решать вопросы о возможности, направлении и пределе самопроизвольного протекания процессов. Термодинамика основана на применении таких величин, как внутренняя энергия U, энтальпия Н, энтропия S, изохорно-изотермический потенциал F (свободная энергия), изобарно-изотермический потенциал G (энергия Гиббса) и других, являющихся однозначными и непрерывными функциями параметров состояния ( температуры, давления, концентраций).

Внутренняя энергия U – это энергия системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (атомов, молекул, ионов и др.) и

9

энергию взаимодействия этих частиц. В термодинамике и её приложениях представляет интерес не само значение U, а ее изменение при изменении состояния системы. Поэтому обычно принимают во внимание только те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах изменения состояния системы. Понятие введено в

1851 году Томсоном ( лорд Кельвин). В простейшем случае для идеального газа изменение U сводится к изменению кинетической энергии молекул и может быть рассчитано уравнением ∆U = mcV∆T , где cV – удельная теплоемкость газа при постоянном объеме. В общем случае U рассчитывается методами статистической физики.

Энтропия S – функция состояния, введенная в 1865 г. немецким физиком Клаузиусом для определения меры необратимого рассеяния энергии. Клаузиус показал, что процесс превращения теплоты в работу подчиняется определенной физической закономерности - второму закону термодинамики. Самая общая формулировка II закона термодинамики: в замкнутой системе могут протекать только такие процессы, которые сопровождаются либо возрастанием, либо сохранением постоянного значения энтропии, т.е. ∆S 0.

Энтропия и её изменение рассчитываются по уравнениям

где Q - изменение теплоты системы, которое выражается через соответствующие изменения термодинамических параметров системы (Т ,V и т.д.).

Согласно третьему закону термодинамики S → 0 при Т → 0.