7.6. Прохождение микрочастицы через потенциальный барьер

Пусть микрочастица движется вдоль оси X на которой находится прямоугольной формы потенциальный барьер шириной l и высотой U (рис.7.3).

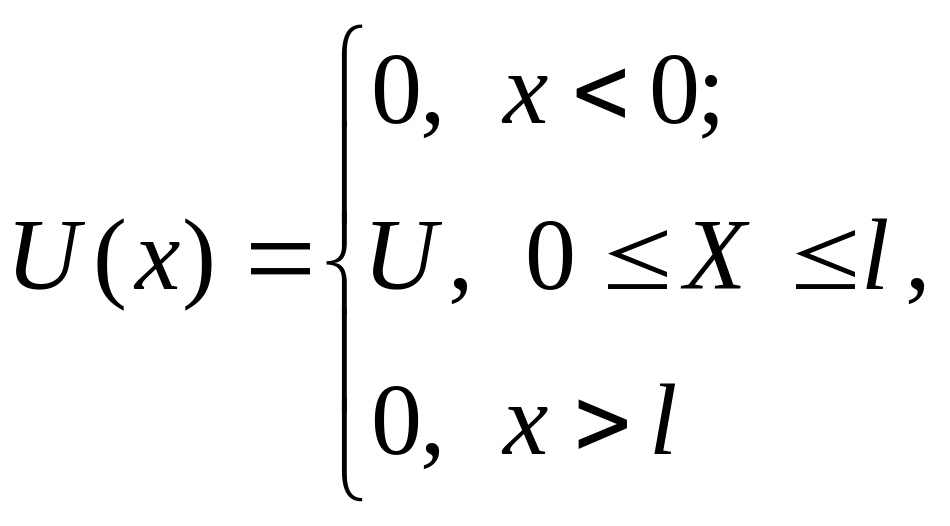
При данных условиях классическая частица либо беспрепятственно пройдёт над барьером при Е>U, либо отразится от него при E<U, и будет двигаться в противоположную сторону.

Для микрочастицы даже при энергии E<U, имеется отличная от нуля вероятность того, что частица окажется в области x>l, т.е. проникнет сквозь барьер.

Квантовая механика приводит к принципиально новому квантовому эффекту, получившего название туннельного эффекта, в результате которого микрочастица может “пройти” сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.

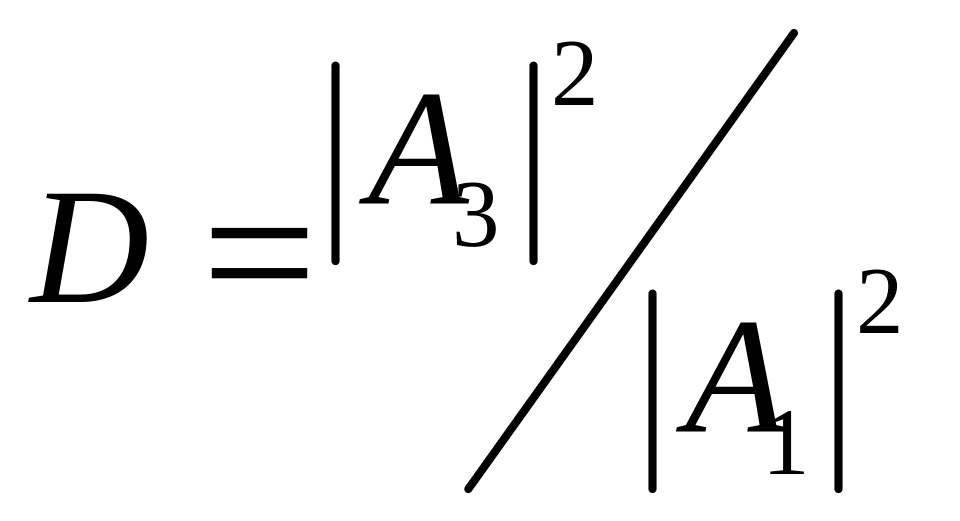, (7.16)

где А₁ и А₃ амплитуды падающей и прошедшей волн де Бройля

Для прямоугольного потенциального барьера коэффициент прозрачности определяется из выражения

, (7.17)

где D₀ – постоянный множитель, который можно принять единице.

Коэффициент прозрачности D сильно зависит от массы частицы m, ширины барьера l и от ; чем шире барьер, тем меньше вероятность прохождения сквозь него барьера.

Для потенциального барьера произвольной формы (см. рис.7.4) для коэффициента прозрачности имеем

, (7.18)

где U=U(x).

Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую не может проникнуть классическая частица, можно объяснить соотношением неопределённостей.

Неопределённость импульса ∆Р на отрезке ∆х=l составляет ∆Р>h/l. Cвязанная с этим разбросом импульса кинетическая энергия (∆Р²/2m) может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше высоты потенциального барьера.

7.7. Атом водорода в квантовой механике

Потенциальная энергия взаимодействия электрона с ядром атома водорода определяется выражением

(7.19)

где r – расстояние между электроном и ядром, e – элементарный заряд.

Графически функция U(r) изображается кривой, представляющей собой гиперболическую потенциальную яму (рис.7.5).

Рассмотрим основные результаты, вытекающие из решения уравнения Шредин- гера для электрона в атоме водорода

1. Энергия электрона принимает ряд дискретных значений, т.е. квантуется

(7.20)

где n = 1, 2, 3… - главное квантовое число.

Самый нижний энергетический уровень электрона в атоме водорода называется основным, все остальные – возбужденными (рис.7.5). При этом каждому E_n (кроме E₁) соответствует несколько волновых функций, отличающихся величиной и ориентацией момента импульса электрона. Различные состояния с одинаковой энергией называются вырожденными, а их число – кратностью вырождения.

2. Момент импульса (орбитальный механический момент) электрона и его проекция на направление внешнего магнитного поля квантуется по законам

L = ħ , (7.21)

L_z = ħ m, (7.22)

где l = 0, 1, 2,…,(n-1) – орбитальное квантовое число; m = 0, 1, 2, …, l – магнитное квантовое число.

При данном значении главного квантового числа n орбитальное квантовое число l принимает n значений, а при данном l магнитное квантовое число m принимает (2l+1) значение.

Квантование проекции вектора L, получившее название пространственного квантования, обусловлено дискретностью ориентации момента импульса во внешнем поле. Графически оно представляется в виде векторных диаграмм (рис.7.6).

Дополнительно к этому, было установлено, что электрон, помимо орбитального, обладает и собственным механическим моментом импульса, получившим название – спин. Значение спина электрона равно

ħ, (7.23)

а его проекция на направление внешнего поля квантуется

L_sz = ħ m_s , (7.24)

где m_s = 1/2 – спиновое квантовое число.

Рис.7.6

Наряду механическими орбитальным и спиновым моментами импульса электрон обладает магнитными орбитальным и спиновым моментами. Величина орбитального магнитного момента и его проекция на направление внешнего магнитного поля квантуется по тем же законам, что и орбитальный механический момент

p_m = gL = _B , (7.25)

p_m = - _B m, (7.26)

где g = e/2m – гиромагнитное отношение, _B = е ħ/2m – магнетон Бора.

Собственный магнитный момент электрона ориентируется по полю или против поля, при этом

p_msz =  _B . (7.27)

Следовательно, магнетон Бора является как бы естественной единицей магнитного момента электрона.

Состояния электрона в атоме принято обозначать следующим образом:

l = 0  s – состояние,

l = 1  p – состояние,

l = 2  d – состояние,

l = 3  f – состояние.

Значение главного квантового числа указывается перед условным обозначением числа l. Например, электрон в состоянии с n = 2 и l = 1 обозначается 2 p, с n = 3 и l = 0 – 3 s и т.д.

В квантовой механике нельзя говорить о траектории движения электрона в атоме. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках объема атома. При этом, боровские стационарные орбиты представляют собой геометрическое место точек, в которых с наибольшей вероятностью может быть обнаружен электрон.