Лекция №15 Нелинейная механика контактных систем

Теоретические вопросы:

15.1. Нелинейная механика

15.2. Метод контактных сил и переносных перемещений для базисной системы гладких тел

15.3. Программирование метода конечных элементов

15.1. Нелинейная механика

В рассмотренных ранее задачах предполагались малые смещения.

В реальных задачах присутствуют нелинейные эффекты, обусловленные как имеющейся геометрией (большие смещения, большие вращения и контакты), так и свойствами материалов (трение, нелинейная упругость, пластичность, ползучесть и т.д.

В таких случаях применяют разбиение внешних условий (смещения, объемные и поверхностные силы) на малые части и решать задачу в несколько этапов.

На каждом этапе внешние условия берутся с множителем таким, что , и нелинейная задача записывается в виде системы

, (15.1)

которая решается последовательными линейными приближениями.

15.2. Метод контактных сил и переносных перемещений для базисной системы гладких тел

Постановка задачи нелинейной механики контактных систем предусматривает исследование трехмерных напряженно-деформированных состояний априорно устойчивых статических контактных систем любого конечного числа линейно-упругих тел, имеющих от нуля до шести кинематических степеней свободы и произвольные – массивные, тонкостенные и комбинированные – конфигурации, взаимные расположения, граничные условия в виде исключения указанных перемещений, варианты технологического и иного нагружения, начальные (про­ектные и изменяющиеся при изнашивании) зазоры, натяги и их сочетания в больших и малых зонах контактов по различным поверхностям.

Дискретизация поверхностей возможного контакта тел осуществляется мно­жествами попарно сопряженных точек, которые могут практически “точ­но” войти в контакт друг с другом в нагруженном состоянии системы. Алгоритмической основой моделирования является метод контактных сил и переносных перемещений. Метод излагается ниже для задач о контакте двух гладких тел. В работе содержится его обобщение на контактные системы любого числа гладких, а в – шероховатых (по Кулону) деталей.

Два трехмерных гладких тела (рис. 39) контактируют при наличии между ними начального зазора ; натяг, если он есть, учитывается как отрицательный зазор. Тело 1 – по условию или предположению – не имеет кинематических степеней свободы; тело 2 имеет таких степеней.

Вводятся две системы отсчета: абсолютная с началом в действительно или условно закрепленной от перемещений точке тела 1 и подвижная с началом в произвольной точке тела 2. При деформировании тел локальные окрестности начала отсчета, а с ними и оси подвижной системы совершают как жесткое целое переносные перемещения, характеризуемые обобщенными координатами (k = 1,...,s), зависящими от выбора начала их отсчета. Перемещения точек тела относительно подвижной системы отсчета происходят за счет его деформирования и далее называются относительными.

На предполагаемых с запасом поверхностях контакта назначаются N пар сопряженных точек – узлов элементов, сетки которых строятся с учетом требований к практическому обеспечению сопряженности. Абсолютные перемещения и сопряженных точек пары i по нормалям к поверхностям тел 1 и 2 не должны в сумме превышать зазора

(15.2)

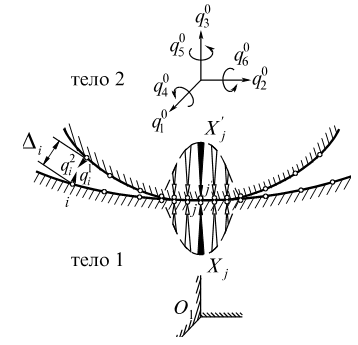
Рис. 39. Контактная базисная система двух тел: нормальные узловые силы, обобщенные координаты и начальные зазоры

Выражения и записываются на основе классической идеи метода сил. Для гладких тел такими силами являются нормальные контактные силы в узлах пар . В варианте раздельного кодирования значения и различаются тем, что в , относящееся к кинематически подвижному телу, помимо относительной компоненты за счет деформируемости, входит заранее неизвестное переносное перемещение по нормали узла i тела 2.

Условие контактирования сопряженных узлов пары i имеет вид:

(15.3)

где  – коэффициенты влияния каждого из тел (n= 1,2) в сопряженных узлах по нормалям;

– перемещения узлов по тем же направлениям при деформировании тела n заданной нагрузкой.

Величины и зависят от условий закрепления тел, а перемещение – от выбора начала отсчета осей тела 2. Перемещения выражаются через координаты с помощью кинематической матрицы [A], определяющей соотношение {qe} = [A]{q0}; из последнего вытекает смысл коэффициентов Aik как перемещений узла i тела 2 вдоль соответствующей нормали при перемещении этого тела на .

Система N уравнений излагаемого метода

(15.4)

содержит N+s неизвестных: N сил Xj и s перемещений – компонентов { }.

N уравнений (15.4) дополняются s уравнениями равновесия тела 2:

(15.5)

где P_m – суммы проекций (m = 1,2,3) и моментов (m = 4,5,6) заданных сил по отношению к координатным осям.

Система уравнений (2.3) и (2.4) является основой базисного алгоритма рассматриваемого метода. Контактные силы нахо­дятся итерационным путем. Узлы, в которых по расчету на данном этапе получаются Xi < 0, остаются в числе контактных и на следующем этапе, где исключаются узлы с Xi > 0. На каждом этапе проверяются условия взаимного непроникания тел в узлах вне зоны контролируемого контакта.

Итерационный поиск завершается, когда очередной этап не выявляет необходимости изменения зоны контакта. От совместного действия за­данных и контактных сил выполняется моделирование тел по МКЭ. Обобщение приведенного базисного алгоритма на систему любого конечного числа тел порождает математическую модель, основой ко­то­рой являются уравнения для двух любых взаимодействующих тел и приложенных к ним контактных сил, в том числе со стороны "третьих" тел. Описанный метод обеспечивает минимизацию общего объема вычислений: итерационный поиск зон контактов осуществляется прямым решением последовательно корректируемых систем линейных уравнений минимально возможного порядка, практически равного общему числу пар сопряженных узлов. Такой путь является принципиально более экономичным, чем известные методы квадратичного программирования.

15.3. Программирование метода конечных элементов

Как уже упоминалось выше, метод конечных элементов (МКЭ) предназначен для приближенного решения практических любых систем уравнений: алгебраических, дифференциальных и интегральных. МКЭ широко распространен в различных областях знаний: в механике, термодинамике, гидродинамике, газодинамике и т.д., т.е. в тех областях где невозможно получить аналитическое решение.

Широкому применению метода конечных элементов для растущего многообразия задач способствуют:

а) внутренняя общность метода;

б) его естественная формулировка в матричной форме;

в) наличие эффективных процедур для решения очень больших систем уравнений;

г) возможности современных вычислительных машин.

Предварительно произвольная система уравнений должна быть преобразована в систему линейных алгебраических уравнений, имеющих матричный вид . Здесь P - вектор правых частей уравнений,  – вектор неизвестных, K – симметричная матрица коэффициентов при неизвестных. Получение такой системы уравнений является очень непростой задачей, но ее решение уже известно для всех важных прикладных задач.

В упругой задаче теории упругости, которая используется при проектировании кузнечно-штамповочных машин, уравнение представляет собой запись закона Гука в обобщенной форме. Алгоритм решения таких задач состоит из следующих этапов:

1. Упругое тело разбивается на элементы. Объемное тело на тетраэдры или параллелепипеды. Плоское тело – на треугольники и прямоугольники.

2. Для каждого элемента составляется матрица жесткости K с использованием функции формы. Функция формы представляет собой способ аппроксимации неизвестной функции .

3. Матрицы жесткости элементов объединяются в единую матрицу жесткости для всего тела.

4. Решая систему уравнений , находят узловые перемещения .

5. С помощью уравнений теории упругости определяются деформации и напряжения.

Кропотливой и трудоемкой задачей МКЭ является задача составления матрицы индексов. Стратегию программирования метода конечных элементов можно представить в виде блок-схемы, показанной на рис. . Как правило, такие программы являются гибридными. В их основе лежит объединение по узлам, которое легко может быть заменено поэлементным объединением, поскольку элементные матрицы жесткости k вычисляются и сохраняются в памяти для последующего использования.

Так как в рассматриваемой программе объединение элементных матричных уравнений проводится по узлам, то необходимо знать элементы, окружающие каждый узел. Эта информация хранится в специальном массиве, который формируется следующим образом.

Сначала в первый столбец записываются нули, первым обрабатывается элемент 1, у которого, глобальными номерами узлов являются числа 1, 8 и 7.

В массиве общее число элементов, окружающих каждый из указанных узлов, при этом увеличивается на единицу. Номер элемента, а именно 1, записывается в следующем столбце (т.е. втором) для каждого из этих узлов.

Следующий элемент (2) с номерами узлов 1, 2 и 8 обрабатывается аналогичным образом. Общее число окружающих элементов получается для этих узлов увеличением на единицу, а номер элемента, а именно 2, записывается в следующем столбце. В результате последовательной обработки массив формируется полностью.

Автоматизация процедур расчетов координат узлов, матрицы индексов и граничных условий позволяет легко изменять количество узлов.

Матрица жесткости системы (всего тела) формируется с помощью матрицы индексов.

Учет граничных условий сопровождается перестройкой матрицы жесткости системы и вектора сил.

Узловые перемещения системы определяются путем обращения матрицы жесткости. Узловые перемещения элементов определяются путем поворотного присваивания значений перемещений системы по матрице индексов.

По уравнениям теории упругости деформации , где u – вектор перемещений. По уравнению связи узловых перемещений D и перемещений u произвольной точки . Отсюда деформация элемента .

По физическим уравнениям теории упругости (закон Гука) вычисляются напряжения .

Сложность расчета состоит в аккуратном использовании индексов элементов, узлов, столбцов, строк, присвоении индексам значений, взятых из матрицы индексов.

Напряжения в узлах определяются как средне-арифметическое напряжений деформаций во всех элементах, сходящихся в узле.

Вопросы для самоподготовки:

1. Что такое нелинейность и в чем заключаются особенности решения задач нелинейной механики?

2. Охарактеризуйте метод контактных сил и переносных перемещений для базисной системы гладких тел?

3. В чем заключаются особенности программирования метода конечных элементов?