Глава 7. Колебания
7.1. Гармонические колебания
Рассмотрим равномерное движение точки D по окружности
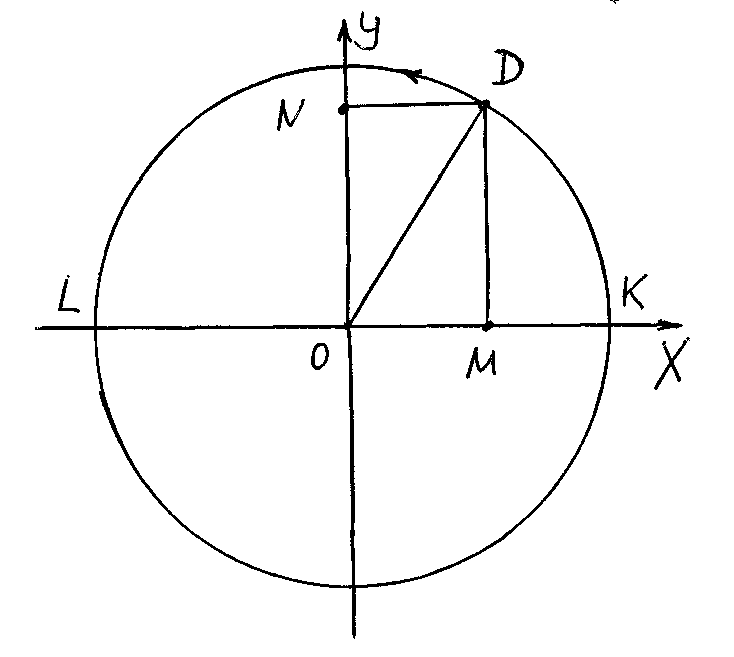
Рис. 47
По мере движения точки D по окружности проекция этой точки на диаметр LK будет двигаться от точки К к точке L и обратно, т.е. совершать колебательные движения.
(7.1)
Уравнение движения т. М:
(7.2)
Если
,
то
(7.3)
Функция
- простейшая периодическая функция с
периодом
.
Тогда можно записать:
(7.4)
Таким образом, точка М будет совершать периодические колебания. Подобные колебания, при которых смещения точки подчиняются закону синуса или косинуса называются гармоническими.
Можно доказать, что точка N будет обладать похожим характером колебаний:
(7.5)
А - амплитуда – максимальная величина смещения.
- доля, которую
смещение х составляет от максимального
– фаза.
-
начальная
фаза.
- угловая частота гармоничных колебаний.
Число колебаний в единицу времени (частоту) можно связать с угловой частотой:
(7.6)
(7.7)
Найдем значения скорости и ускорения точки, совершающей гармонические колебания:
(7.8)
(7.9)
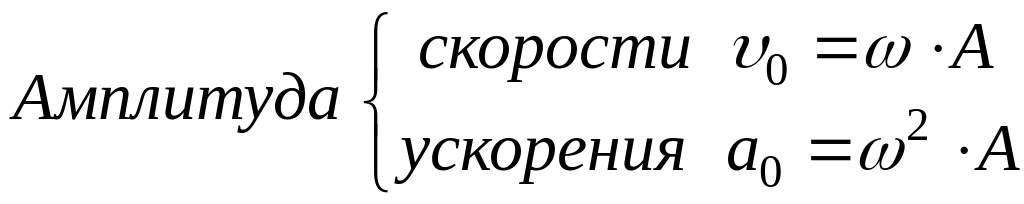
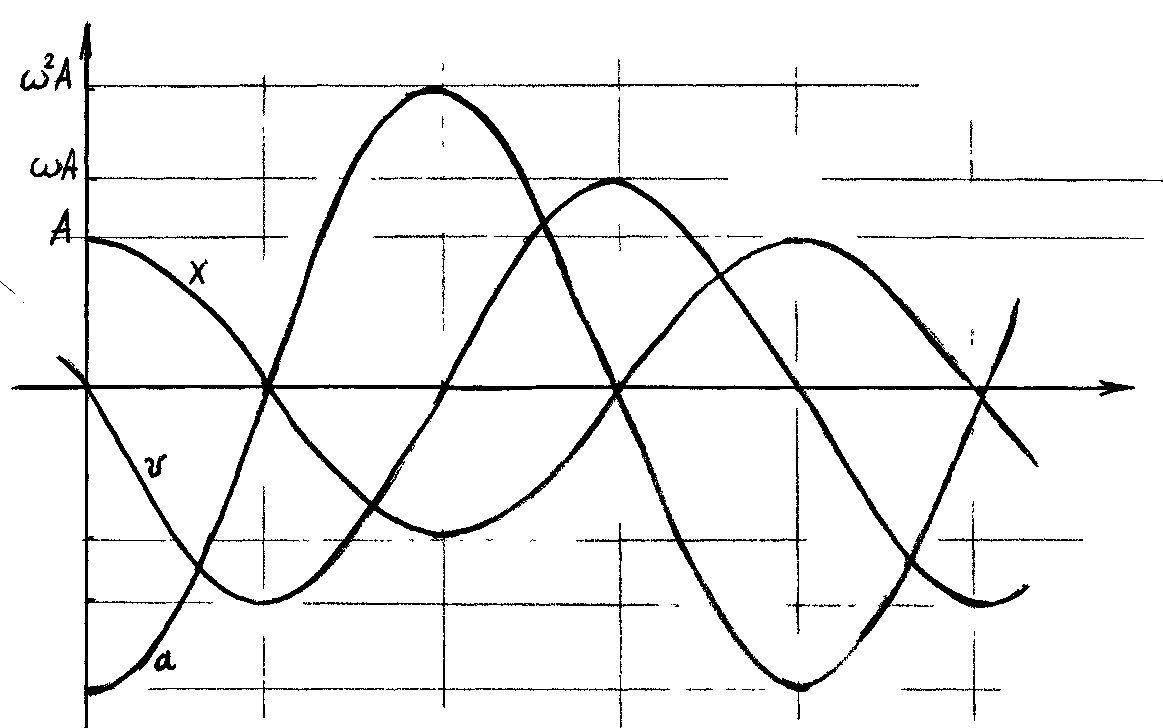
Рис. 48
7.2. Упругие и квазиупругие силы
Согласно
второму закону Ньютона
;
тогда, учитывая, что
,
можно записать:
(7.10)
Здесь
согласно (7.3).
Отсюда следует, что:
,
(7.11)
где
(7.12)
Таким образом, сила, вызывающая гармонические колебания, обладает следующими свойствами:
1) Величина силы прямо пропорциональна смещению точки от центра колебания.
2) Направление силы противоположно направлению смещения.
Рассмотрим колебание тела на пружине, расположенной в горизонтальной плоскости.
Нам
известно, что
при любых смещениях.
Из (7.12) следует, что
Отсюда:
(7.13)
С другой стороны:
.
(7.14)
Приравнивая правые части уравнений (7.13) и (7.14), получим выражение для периода колебаний тела на пружине:
(7.15)
Для груза, подвешенного на пружине:
(7.16)
Во всем остальном будет наблюдаться полная аналогия с предыдущим случаем: возникнет аналогичное гармоническое колебание. Однако теперь положение равновесия груза будет отвечать несколько растянутому состоянию пружины.
Можно доказать, что материальная точка будет совершать гармонические колебания даже, если на нее не действует упругая сила, достаточно, чтобы эта сила подчинялась закону:
Квазиупругая сила (quasi - как бы) – сила, не являющаяся по своей природе упругой, подчиняющаяся закону .
Рассмотрим решение дифференциального уравнения одномерного движения возникающего под действием только одной квазиупругой силы.
Из второго закона Ньютона получим:
(7.17)
(7.18)
Получили однородное дифференциальное уравнение второго порядка, решением которого является
(7.19)
Найдем первую и вторую производную от данного выражения:
(7.20)
(7.21)
Подставим найденные производные в исходное дифференциальное уравнение:
(7.22)
Сократив
на
,
получим:
.
Подобное выражение для было получено ранее при рассмотрении движения под действием сил упругости. Таким образом, мы доказали, что и под действием квазиупругой силы будут совершаться гармонические колебания.