Выводы моментов инерции тел вращения

Обруч (кольцо)

Разобьем длину обруча на элементарные массы (рис.22).

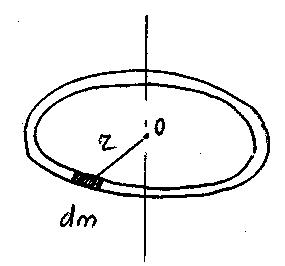
Рис.22

то (5.13)

Цилиндр

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины (элементарные цилиндры с внутренним радиусом и внешним ) (рис.23).

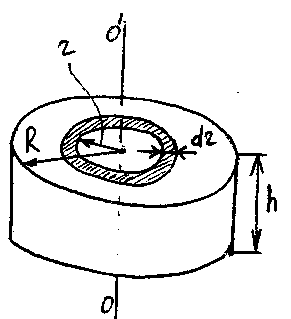
Рис.23

Для каждого отдельного цилиндра момент инерции равен:

,

где - масса всего элементарного цилиндра. Сечение стенки полого цилиндра: , а ее длина ; поэтому объем элементарного цилиндра равен .

Если материал однороден, то масса всего полого цилиндра:

, где - плотность материи.

Таким образом

,

но - это объем цилиндра.

Тогда масса цилиндра , а его момент инерции:

(5.14)

Стержень

Пусть стержень совершает вращательное движение относительно оси, проходящей через центр инерции перпендикулярно оси стержня. Разобьем стержень на элементарные массы, как это показано на рис.24.

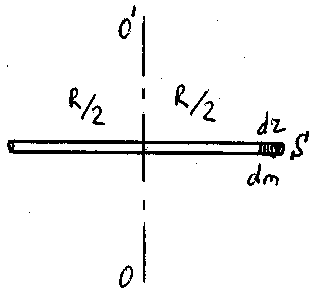
Рис.24

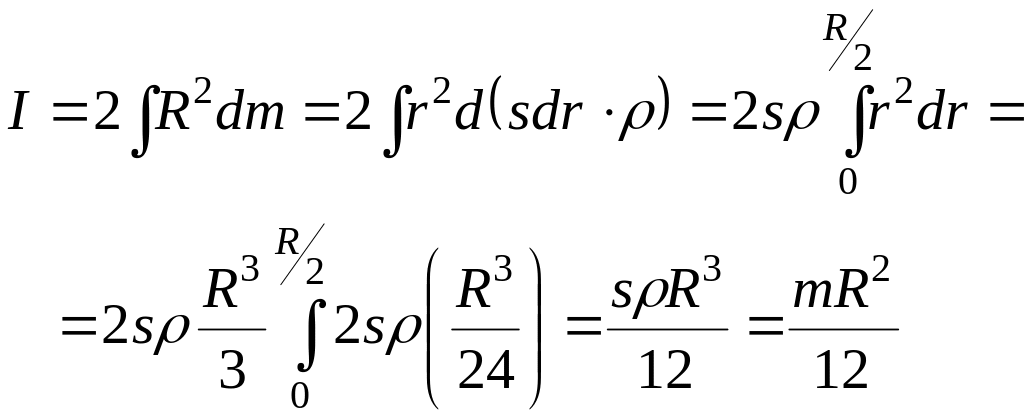
Таким образом:

(5.15)

Шар

Выделим элементарный объем в виде цилиндра радиус высотой (рис.25).

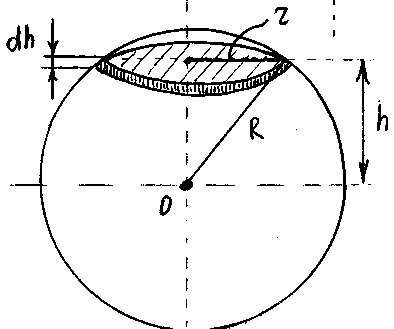
Рис.25

Таким образом (5.16)

Чтобы найти момент инерции относительно произвольной оси можно воспользоваться теоремой Штейнера:

Момент инерции I относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями:

(5.17)

5.3. Момент импульса

Тело движущееся прямолинейно, обладает импульсом . По отношению к некоторой точке, оно так же обладает моментом импульса равным (рис.26). Модуль векторного произведения этих векторов равен произведению импульса и кратчайшего расстояния до траектории.

(5.18)

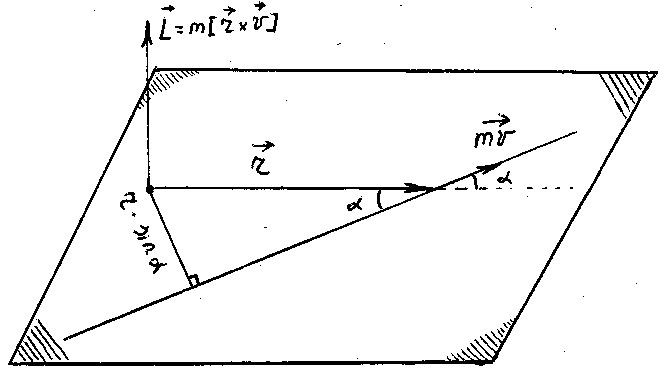
Рис.26

Момент импульса, которым обладает тело, движущееся прямолинейно и равномерно, есть величина постоянная. Действительно, хотя радиус-вектор все время изменяется, но момент импульса остается постоянным, так как остается неизменной длина перпендикуляра, опущенного из этой точки на направление вектора .

Но особый интерес представляют случаи, когда импульс изменяется, а момент импульса относительно какой-либо оси остается постоянным. Простейшим примером этого случая является движение тоски по окружности с постоянной скоростью. Так как направление скорости при этом все время изменяется, то вектор импульса также изменяется (по направлению, но не по величине).

Если за ось моментов выбрать ось проходящую через центр вращения, то момент импульса относительно этой оси будет оставаться постоянным. Вектор импульса будет направлен все время по оси и по величине равен произведению постоянных величин и (угол между и все время остается прямым).

Однако, если за ось моментов выбрать ось, не проходящую через центр окружности, то момент импульса относительно этой оси не будет постоянным, так как в векторном произведении будет изменятся величина и угол между и .

Таким образом, можно сделать вывод:

материальная тоска, движущаяся по окружности, не является замкнутой системой, так как на нее все время должна действовать какая-либо внешняя сила, сообщающая ей центростремительное ускорение (например, натяжение нити, которая прикреплена к оси вращения). Эта сила и изменяет импульс, но не изменяет момента импульса материальной точки относительно оси, проходящей через центр вращения.

Установим теперь связь между моментом внешних сил и моментом импульса.

Пусть на материальную точку массы действует сила .

(5.19)

Домножем векторно обе части равенства на

(5.20)

Правая часть представляет собой момент сил относительно выбранной оси.

(5.21)

Здесь - есть элементарное изменение радиус-вектора, т.е. элементарное перемещение точки за время , и, значит, .

Таким образом, первый член в правой части (5.21) есть векторное произведение 2-х коллинеарных векторов ( и ), которое, как известно, равно нулю. Следовательно:

Поэтому уравнение (5.20) можно переписать следующим образом:

или - уравнение моментов (5.22)

т.е. производная по времени от момента импульса материальной точки относительно какой-либо неподвижной оси равна моменту действующих на материальную точку сил относительно этой оси. В частности, если , то

(5.23)

Уравнение (5.22) справедливо для любой произвольно выбранной произвольной оси. Для случая вращения по окружности, если ось моментов есть ось, проходящая через центр окружности:

(5.24)

Тогда уравнение (5.22) примет вид

- момент инерции.

(5.25)

Получим знакомое уравнение , выражающее основной закон динамики вращающего движения.

(5.26)

Уравнение (5.26) справедливо для любых неподвижных осей и для случая, когда движение происходит не по окружности.