
- •Общая физика в задачах
- •Механика. Молекулярная физика и термодинамика.
- •Электричество и магнетизм
- •Сборник задач
- •А.В. Калач [и др.]; Воронежский гасу. – Воронеж, 2012. – 181 с.
- •Рецензенты:
- •Введение
- •Глава 1. Сведения о векторах теоретические сведения
- •Задачи для самостоятельного решения
- •Глава 2. Физические основы механики теоретические сведения Кинематика поступательного и вращательного движения
- •Мгновенная скорость:
- •Динамика материальной точки и поступательного движения абсолютно твёрдого тела
- •Работа и энергия
- •Вращательное движение абсолютно твёрдого тела
- •Тяготение. Элементы теории поля
- •Сила тяжести:
- •Механика жидкостей и газов
- •Релятивистская механика
- •Примеры решения задач Кинематика поступательного и вращательного движения
- •Динамика материальной точки и поступательного движения абсолютно твёрдого тела
- •Работа и энергия
- •Вращательное движение абсолютно твёрдого тела
- •Момент инерции маховика в виде сплошного диска определяется формулой
- •Тяготение. Элементы теории поля
- •Механика жидкостей и газов
- •Релятивистская механика
- •Задачи для самостоятельного решения Кинематика поступательного и вращательного движения
- •Динамика материальной точки и поступательного движения абсолютно твёрдого тела
- •Работа и энергия
- •Вращательное движение абсолютного твердого тела
- •Тяготение. Элементы теории поля
- •Механика жидкостей и газов
- •Релятивистская механика
- •Глава 3. Молекулярная физика и термодинамика теоретические сведения Молекулярно-кинетическая теория идеальных газов
- •Основы термодинамики
- •Примеры решения задач Молекулярно-кинетическая теория идеальных газов
- •Основы термодинамики
- •Задачи для самостоятельного решения Молекулярно-кинетическая теория идеальных газов
- •Основы термодинамики
- •Глава 4. Электричество и магнетизм теоретические сведения Электростатика
- •Постоянный электрический ток. Электрические токи в металлах, жидкостях, вакууме и газах
- •Плотность тока насыщения:
- •Магнитное поле
- •Закон Био-Савара-Лапласа
- •Электромагнитная индукция
- •Магнитное поле в веществе
- •Движение заряженных частиц в магнитном поле
- •Примеры решения задач Электростатика
- •Постоянный электрический ток. Электрические токи в металлах, жидкостях, вакууме и газах
- •Магнитное поле
- •Электромагнитная индукция
- •Магнитное поле в веществе
- •Движение заряженых частиц в магнитном поле
- •Электростатика
- •Постоянный электрический ток. Электрические токи в металлах, жидкостях, вакууме и газах
- •Магнитное поле
- •Электромагнитная индукция
- •Магнитное поле в веществе
- •Движение заряженных частиц в магнитном поле
- •Ответы сведения о векторах
- •Физические основы механики Кинематика поступательного и вращательного движения
- •Динамика материальной точки и поступательного движения абсолютно твердого тела
- •Работа и энергия
- •Динамика вращательного движения абсолютно твёрдого тела
- •Тяготение. Элементы теории поля
- •Механика жидкостей и газов
- •Релятивистская механика
- •Молекулярная физика и термодинамика Молекулярно-кинетическая теория идеальных газов
- •Основы термодинамики
- •Электричество и магнетизм Электростатика
- •Постоянный ток. Электрические токи в металлах, жидкостях, вакууме и газах
- •Магнитное поле
- •Электромагнитная индукция
- •Магнитное поле в веществе
- •Движение заряженных частиц в магнитном поле
- •Библиографический список
- •Справочные сведения
- •1. Фундаментальные физические постоянные
- •2. Греческий алфавит
- •3. Сведения о Солнце, Земле и Луне
- •4. Множители и приставки си для десятичных кратных и дольных единиц
- •5. Плотность ρ, 103 кг/м3, некоторых веществ
- •6. Диэлектрическая проницаемость ε некоторых веществ
- •7. Удельная теплоемкость с, 103 Дж/(кг⋅к), некоторых веществ
- •8. Удельное сопротивление ρ, 10-8 Ом·м, некоторых веществ (при 20 0с)
- •Оглавление
- •Общая физика в задачах
- •Механика. Молекулярная физика и термодинамика.
- •Электричество и магнетизм
- •Сборник задач
- •3 94006 Воронеж, ул. 20-летия Октября, 84
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Воронежский государственный архитектурно-строительный университет»
Общая физика в задачах
Механика. Молекулярная физика и термодинамика.
Электричество и магнетизм
Сборник задач
Рекомендовано научно-методическим советом Воронежского ГАСУ
в качестве учебного пособия для студентов
направления 280700 «Техносферная безопасность»
Воронеж – 2012
УДК 53(07)
ББК-22.3я7
О-28
Авторский коллектив:
А.В. Калач, А.К. Тарханов,
О.Б. Рудаков, А.И. Никишина, Е.В. Алексеева
Общая физика в задачах. Механика. Молекулярная физика и
О-28 термодинамика. Электричество и магнетизм: учебн. пособие/
А.В. Калач [и др.]; Воронежский гасу. – Воронеж, 2012. – 181 с.
ISBN 978-5-89040-429-9
Настоящее учебное пособие предназначено для студентов полной и сокращенной форм обучения. Приведены краткие теоретические сведения, примеры решения и условия задач по темам «Механика», «Молекулярная физика и термодинамика», «Электричество и магнетизм». Ко всем задачам приведены ответы.
Ил. 43. Табл. 2. Библиогр.: 11 назв.
Рецензенты:
кафедра физики и теплообменаУральского института ГПС МЧС России;
Булгаков В.И., к.т.н., зав. кафедрой физики Академии гражданской
защиты МЧС России
УДК 53(07)
ББК 22.3я7
ISBN 978-5-89040-429-9
© Калач А.В., Тарханов А.К.,
Рудаков О.Б., Никишина А.И.,
Алексеева Е.В., 2012
© Воронежский ГАСУ, 2012


Введение
Предлагаемый сборник предназначен для студентов, обучающихся в бакалавриате по направлению «Техносферная безопасность». Разнообразие подобранных задач позволяет студентам изучать физические явления и законы с разных сторон, формировать глубокие представления о фундаментальных физических явлениях и их практическом использовании.
Выбор тематики и распределение задач по трудности обусловлены учебным планом, однако оставляют возможность использовать этот задачник студентам и преподавателям различных высших учебных заведений, колледжей и лицеев.
Составители учебного пособия использовали не только собственные разработки, но и прошедшие широкую апробацию в студенческой аудитории задачи, представленные в учебных пособиях Трофимовой Т.И., Савельева И.В., Сивухина Д.В., Леденева А.Н., Серова И.К., Чертова А.Г. и др.
Структура сборника задач представляется логичной и последовательной, состоит из введения, четырех глав, каждая из которых содержит теоретические сведения, примеры решения задач, задачи для самостоятельного решения. В конце учебного пособия представлены таблицы, содержащие краткие математические сведения и необходимый набор физических констант, ответы к задачам. Выбор формул и краткость их пояснения рассчитана на студентов, знакомых с материалами данного раздела. Все формулы и ответы приведены в системе СИ. В конце учебного пособия приведены наиболее часто используемые математические соотношения, основные физические константы и справочные таблицы. Предлагаемый материал призван помочь усвоению теоретических знаний. Самостоятельное выполнение контрольных заданий способствует более глубокому пониманию курса физики и закреплению его в памяти.
Глава 1. Сведения о векторах теоретические сведения
Механическое движение – изменение с течением времени взаимного расположения тел или их частей.
В механике (физике) для описания движения тел в зависимости от условий конкретных задач используют физические модели.
Материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.
Абсолютно твердое тело – тело, которое ни при каких условиях не может деформироваться, и при всех условиях расстояние между двумя точками (или, точнее, между двумя частицами) этого тела остается постоянным.
Положение материальной точки определяется по отношению к некоторому, произвольно выбранному телу, называемому телом отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом отсчета.
 С
С
Рис. 1
 истема
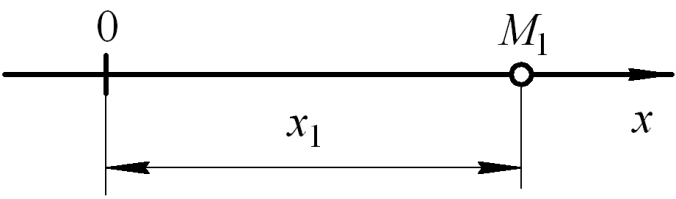
координат. Чтобы задать положение
точки, лежащей на прямой линии, выбирают
произвольно начало отсчета (точка 0 на
рис. 1), единицы масштаба и одно из двух
возможных направлений в качестве
положительного. Такая прямая называется
координатной прямой. Полупрямая,
идущая в положительном направлении,
называется положительной полуосью;
полупрямая, идущая в противоположном
направлении, – отрицательной полуосью.
Координатой точки М1, находящейся
на оси, называют расстояние х1
от начала отсчета, взятое со знаком
плюс, если точка лежит на положительной
полуоси, или со знаком минус, если точка
лежит на отрицательной полуоси.
истема
координат. Чтобы задать положение
точки, лежащей на прямой линии, выбирают
произвольно начало отсчета (точка 0 на
рис. 1), единицы масштаба и одно из двух
возможных направлений в качестве
положительного. Такая прямая называется
координатной прямой. Полупрямая,
идущая в положительном направлении,
называется положительной полуосью;
полупрямая, идущая в противоположном
направлении, – отрицательной полуосью.
Координатой точки М1, находящейся
на оси, называют расстояние х1
от начала отсчета, взятое со знаком
плюс, если точка лежит на положительной
полуоси, или со знаком минус, если точка
лежит на отрицательной полуоси.
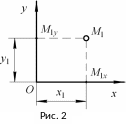
Для того чтобы задать числами положение точки на плоскости, выбирают на ней две координатных оси, пересекающиеся, вообще говоря, под произвольным углом (отличным от 00 и 1800). Мы будем использовать две взаимно перпендикулярные оси, образующие декартову, или прямоугольную, систему координат. Одну ось назовем осью x, другую – осью y. Точку пересечения осей называют началом координат, оно является началом отсчета каждой из координатных осей (рис. 2). Пусть М1 – произвольная точка на плоскости. Спроектируем точку на координатные оси, т.е. проведем через М1 перпендикуляры к прямым Оx и Оy и обозначим основание этих перпендикуляров соответственно М1х и М1y. Координатами х1 и y1 точки М1 называют координаты точек М1х и М1y.
 П
П
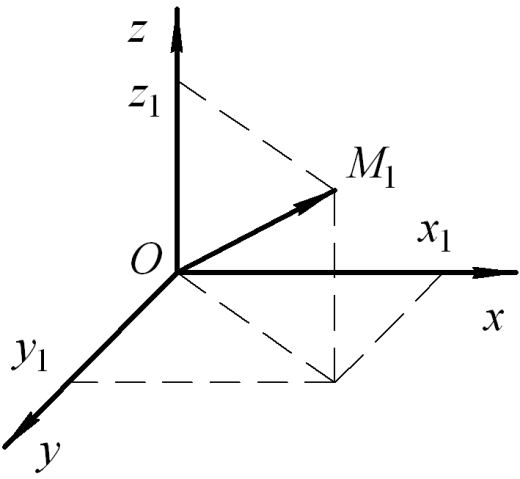
оложение точки М1 в пространстве определяется координатами х1, y1, z1 основания перпендикуляра, опущенного на три взаимно перпендикулярные координатные оси Оx, Oy, Oz (рис. 3).
П
Рис. 1.3
Рис. 3
ри движении материальной точки ее координаты с течением времени изменяются. В общем случае движение определяется скалярными уравнениями (они называются параметрическими):x = x(t), y = y(t), z = z(t),
эквивалентными векторному уравнению
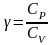 .
.
Скалярной величиной называется величина, значение которой определяется только положительными и отрицательными числами. Примерами таких величин являются масса, заряд, плотность, работа и т.д.
Векторной величиной называется направленный отрезок прямой (рис. 4). Точка О называется началом вектора, А – концом вектора. Длина отрезка
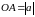
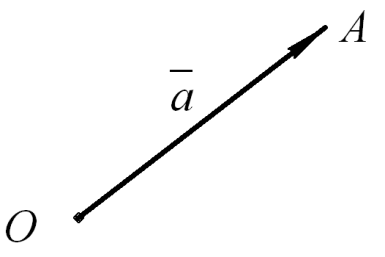 н
н
Рис. 4
азывается величиной или модулем вектора. Следовательно, вектор характеризуется направлением и модулем. Два вектора равны друг другу, если они имеют равные модули и одинаковые направления. Над обозначением вектора принято сверху ставить стрелочку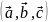 ,
при обозначении модуля символ вектора
пишут в вертикальных черточках
,
при обозначении модуля символ вектора
пишут в вертикальных черточках
 .
.
Умножение
вектора на скаляр. В результате
умножения вектора
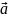 на скаляр d получается новый вектор:
на скаляр d получается новый вектор:
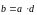 ,
,
модуль которого в | d | раз больше, чем a:
b = | d | a.
При положительном
d направление вектора
 совпадает с направлением вектора
,
при отрицательном d его направление
противоположно
.
совпадает с направлением вектора
,
при отрицательном d его направление
противоположно
.
Сложение векторов. Правило треугольников: векторы и (рис. 5) переносятся параллельно самим себе так, чтобы конец одного вектора совместился с началом другого вектора, тогда вектор (рис. 5 б), проходящий через начало первого вектора и конец другого вектора, равен сумме этих векторов:
 .
.
Эта сумма называется векторной.
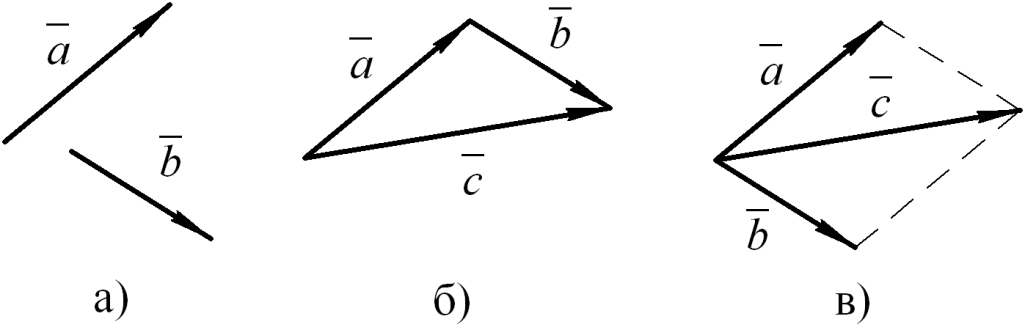
Рис. 5
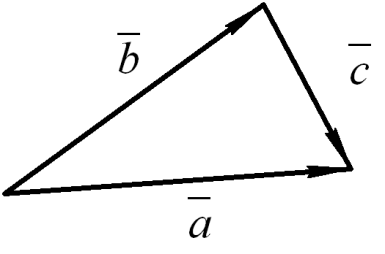 Правило
параллелограмма. Векторы
и
переносятся параллельно самим себе
так, чтобы начала их совместились (рис.
5, в), сумма векторов будет изображаться
диагональю параллелограмма, построенного
на этих векторах.
Правило
параллелограмма. Векторы
и
переносятся параллельно самим себе
так, чтобы начала их совместились (рис.
5, в), сумма векторов будет изображаться
диагональю параллелограмма, построенного
на этих векторах.
Р
Рис. 6
азность векторов. Начала векторов и совмещаются (без изменения их направления), затем проводится вектор от конца вычитаемого вектора к концу уменьшаемого вектора (рис. 6); этот вектор будет равен разности векторов: .
.
Проекции векторов на оси координат. Проекцией вектора на любую ось (х, y, z) называется произведение модуля вектора на косинус угла между вектором и положительной полуосью х (y, z) (рис. 7):
PQ
=
 cos
cos
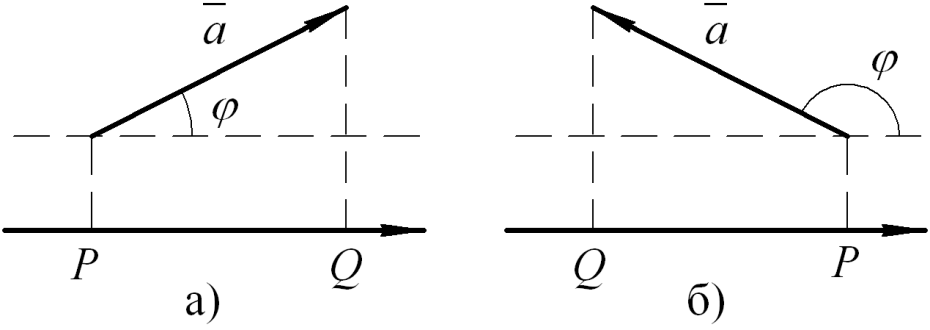
Рис. 7
Проекция вектора положительна, если угол острый (рис. 7, а), отрицателен, если угол тупой (рис. 7, б), и равна нулю, если угол прямой.
Координатами ах, аy, аz вектора в прямоугольной системе координат xyz в пространстве называется его проекции на координатные оси x, y, z:
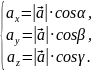
Здесь
 – углы между вектором и осями. Вектор
с координатами ах, аy,
аz записывается в виде
– углы между вектором и осями. Вектор
с координатами ах, аy,
аz записывается в виде
 (ах,
аy, аz).
(ах,
аy, аz).
Проекции вектора АВ, заданного двумя точками А (x1, y1, z1) и В (x2, y2, z2), равны разностям соответствующих координат точек:

Модуль вектора вычисляется по формуле
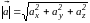 ,
,
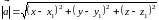 .
.
В

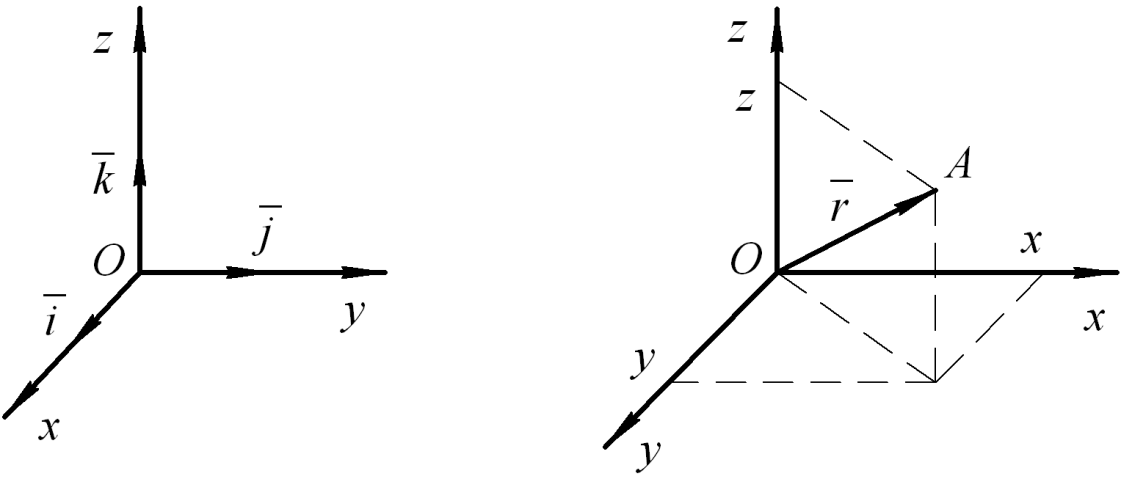 ведем
орты координатных осей, т.е. единичные
векторы
ведем
орты координатных осей, т.е. единичные
векторы
 (рис. 8). Вектор называется единичным,
если его модуль равен единице.
(рис. 8). Вектор называется единичным,
если его модуль равен единице.
Рис. 8 Рис. 9
Используя единичные векторы, можно представить вектор в виде
 .
.
Радиус-вектором
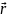 точки называется вектор, проведенный
из начала координат в данную точку А.
Его проекции на оси равны координатам
(рис. 9):
точки называется вектор, проведенный
из начала координат в данную точку А.
Его проекции на оси равны координатам
(рис. 9):
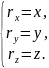
Радиус-вектор можно представить в виде
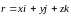 ,
,
а его модуль равен:
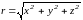 ,
,
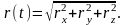
 Скалярным
произведением
Скалярным
произведением
 векторов
и
называется скаляр, равный
произведению модулей этих векторов на
косинус угла
между ними (рис. 10):
векторов
и
называется скаляр, равный
произведению модулей этих векторов на
косинус угла
между ними (рис. 10):
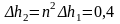 .
.
С
Рис. 10
калярное произведение векторов и величина скалярная.Векторное
произведение
 двух векторов
и
образует новый вектор
двух векторов
и
образует новый вектор
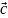 ,
направленный перпендикулярно к плоскости,
в которой лежат векторы
и
(рис. 11), равный по модулю произведению
их модулей на синус угла
между ними:
,
направленный перпендикулярно к плоскости,
в которой лежат векторы
и
(рис. 11), равный по модулю произведению
их модулей на синус угла
между ними:
c = ab sin .
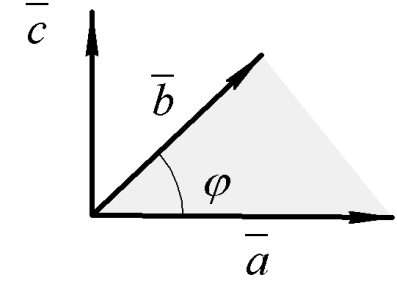 Н
Н
Рис. 11
аправление вектора можно определить по правилу правого винта: если поворот головки винта соответствует повороту вектора к вектору по наименьшему углу, то поступательное перемещение винта будет указывать направления вектора . Векторы типа , направление которых связывается с направлением вращения, называются псевдовекторами. При определенном условии, например при переходе от правой системы координат к левой, направление псевдовекторов изменяется на обратное, истинные векторы при этом направления не меняют.
