
Учебное пособие 1865
.pdf
|
sh z = |
ez −e−z |
, |
ch z = |
ez +e−z |
, |
|
||||
|
2 |
2 |
|
(4.5) |
|||||||
|
sh z |
|
|
|
|
|
ez +e−z |
||||
th z = |
= |
|
ez −e−z |
, |
cth z = |
ch z |
= |
. |
|||
ch z |
ez +e−z |
sh z |
ez −e−z |
||||||||
|
|
|
|
|
|
||||||
Они весьма просто выражаются через тригонометрические функции:
sh z = −i sin iz, |
ch z = cos iz, |
th z = −itgiz, |
cth z = ictgi z , |
и поэтому несущественно отличаются от последних.
Пример 4.6. Найти Arcsin 2.
Решение. По формуле (4.4)
Arcsin 2 = |
π |
−iLn(2 ± 3); |
|
2 |
|
(мы поставили "±" перед корнем, поскольку 3 обычно понимается как арифметическое значение корня). Для вычисления логарифма используем формулу (4.5), в которой
полагаем |
|
z |
|
= 2 ± |
3, arg z = 0 . |
|
|
|
|
|
|
|
|
||||
Получаем |
|
π |
|
|
||||
Arcsin 2 = π |
−iln(2 ± 3) +2πk = |
±ln(2 + |
3) +2πk, |
|||||
2 |
|
2 |
|
|
||||
где 3 — арифметическое значение корня и k |
— любое целое |
|||||||
число. |
|
|
|
|
4. Функцией Жуковского называется функция |
|
|||
ω = |
1 |
(z + |
1) . |
(4.6) |
|
2 |
|
z |
|
Эта функция имеет важные применения в теории крыла самолета, а также весьма полезна при построении ряда конформных отображений. Она аналитична всюду в , кроме точек z = 0 и z = ∞. Производная
ω′ = 12 (1− z12 )
81

существует всюду в , за исключением точек z = 0 и z = ∞, и обращается в нуль при z = ±1. Поэтому отображение (12.6) конформно всюду, кроме точек 0, ±1 и ∞.
Выясним, при каком условии две различные точки переходят в одну и ту же точку. Пусть z1 ≠ z2 и
1(z1 + 1 ) = 1 (z2 + 1 ) .
2z1 2 z2
Отсюда следует, что |
|
|
|
|
|
|
|
|
|
|||
(z |
+ |
1 |
) −(z |
|
+ |
1 |
) = (z |
− z |
|
)(1− |
1 |
) = 0 . |
|
2 |
|
2 |
|
||||||||
1 |
|
z1 |
|
1 |
|
|
z1z2 |
|||||
|
|
|
|
z2 |
|
|
|
|||||
Так как z1 ≠ z2 |
, то это равенство равносильно условию |
|||||||||||
|
|
|
|
|
|
|
z1z2 |
=1. |
(4.7) |
|||
Поэтому для однолистности функции Жуковского в некоторой области D необходимо и достаточно, чтобы эта область не содержала пары различных точек, удовлетворяющих условию
(4.7). Такими областями являются, например, внешность |
|
|
z |
|
>1 |
|||||||||||
|
|
|||||||||||||||
единичного круга (при этом |
|
z1z2 |
|
>1) и внутренность |
|
|
|
z |
|
|
<1 |
|||||
|
|
|
|
|
|
|
||||||||||
этого круга ( |
|
z1z2 |
|
<1 ). |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
Чтобы наглядно представить себе отображение (4.6), выясним, в какие кривые оно переводит окружности (показаны на рис. 4.9, а сплошными линиями) и лучи (показаны
пунктирами). Положим |
z = reiϕ . |
|
Тогда (4.6) |
перепишется в |
||||||||
виде |
1 |
|
1 e−iϕ ) = |
1 |
(r + 1) cosϕ +i |
1 |
|
1)sinϕ, |
||||
ω = u +iv = |
(reiϕ + |
(r − |
||||||||||
откуда |
2 |
|
r |
|
|
2 |
r |
|
2 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = 1 |
(r + 1) cosϕ, |
|
|
|
|
|||||
|
|
|
|
2 |
|
r |
|
|
|
|
|
(4.8) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
(r − |
1 |
)sinϕ. |
|
|
|
|
|
|
|
v = |
2 |
r |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
82
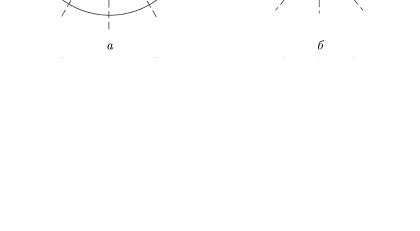
Рассмотрим образы окружностей r = r0 . Из (4.8) следует
cosϕ = |
|
u |
|
, |
sinϕ = |
|
v |
|
. |
1 |
(r + |
1) |
1 |
(r − |
1) |
||||
|
2 |
|
r |
|
2 |
|
r |
||
Рис. 4.9
Возводя эти равенства в квадрат, складывая и полагая r = r0 , получим
|
|
u2 |
|
|
|
|
+ |
|
|
|
v2 |
|
|
|
=1. |
|
|
(4.9) |
|||
|
1 |
(r + |
1 |
)2 |
|
1 |
(r − |
1 |
)2 |
|
|
|
|||||||||
4 |
|
4 |
|
|
|
|
|
|
|||||||||||||
0 |
|
r |
0 |
|
|
r |
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Уравнение (4.9) является уравнением эллипса с полуосями |
|||||||||||||||||||||
a = 1 |
(r + |
1 |
), |
|
|
b = 1 (r − |
1 |
). |
|
||||||||||||
|
|
|
|||||||||||||||||||
r |
2 |
0 |
|
|
r0 |
|
|
|
|
|
r |
2 |
0 |
r0 |
|
||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итак, образами окружностей |
|
|
z |
|
= r0 |
в плоскости z |
будут |
||||||||||||||
|
|
||||||||||||||||||||
эллипсы в плоскости ω (рис. 4.9, б). Если r0 →1 , то ar |
→1, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
br0 → 0 . Поэтому эллипсы будут стягиваться к отрезку [-1,1].
83

При больших |
|
r |
разность |
a |
r |
−b = |
1 |
|
|
мала, и эллипсы мало |
||||||||
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
r |
|
r0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отличаются от окружностей. |
|
|
|
|
|
|
|
|
|
ϕ =ϕ0 , преобразуем |
||||||||
Чтобы |
получить |
образ |
лучей |
|||||||||||||||
равенства (4.8) к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
u |
|
= |
1 |
(r + |
1), |
|
|
|
v |
|
= |
1 (r − |
1). |
|||
|
|
cosϕ |
2 |
|
|
sinϕ |
||||||||||||
|
|
|
|
r |
|
|
|
|
|
2 |
r |
|||||||
Возводя эти равенства в квадрат, вычитая из первого второе и
полагая ϕ =ϕ0 , получим |
|
|
|
||
|
u2 |
v2 |
|
||
|
|
− |
|
=1. |
(4.10) |
|
|
|
|||
|
cos2 ϕ0 |
sin2 ϕ0 |
|
||
Уравнение (4.10) является уравнением гиперболы с полуосями aϕ0 = cosϕ0 , bϕ0 = sinϕ0 . Следовательно, лучи ϕ =ϕ0
отображаются в части гипербол (рис. 4.9, б).
Таким образом, функция Жуковского взаимнооднозначно и конформно отображает внешность единичного круга на внешность отрезка [-1,1].
Из (4.6) легко видеть, что ω(z) =ω(1 z) . Функция ω =1
z) . Функция ω =1 z взаимно-однозначно и конформно отображает внутренность круга z <1 на внешность этого же круга. Отсюда следует, что
z взаимно-однозначно и конформно отображает внутренность круга z <1 на внешность этого же круга. Отсюда следует, что
функция Жуковского взаимно-однозначно и конформно отображает также и внутренность единичного круга на внешность отрезка [-1,1].
84
5. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО 5.1. Интеграл от функции комплексного переменного
Рассмотрим гладкую кривую Г на комплексной плоскости, заданную параметрическими уравнениями
x = x(t), y = y(t), α ≤ t ≤ β |
(1.1) |
Как уже отмечалось, эти уравнения можно записать в компактной форме:
z(t) = x(t) +iy(t), α ≤ t ≤ β |
(1.2) |
При изменении параметра t от α до β соответствующая точка
z(t) будет двигаться по кривой Г. Поэтому уравнения (1.1) и (1.2) не только определяют точки кривой Г, но и задают направление обхода этой кривой. Кривая Г с заданным направлением ее обхода называется ориентированной кривой.
Пусть в области D задана непрерывная функция f(z)= и(х,у) + iv(x,y), и пусть кривая Г лежит в D. Чтобы ввести
понятие интеграла ∫ f (z)dz от функции f(z) по кривой Г,
Г
определим дифференциал dz равенством dz = dx + idy. Подынтегральное выражение преобразуется к виду
f(z) dz = (и + iv)(dx + idy) = (udx — v dy) + i(v dx + и dy).
Таким образом, интеграл от комплексной функции f(z) по кривой Г естественно определить равенством
∫ f (z)dz = ∫udx −vdy +i∫vdx +udy |
(1.3) |
||
Г |
Г |
Г |
|
в правую часть которого входят два действительных криволинейных интеграла второго рода от действительных функций и и v. Для вычисления этих интегралов следует
85

вместо х и у подставить функции x(t) и y(t), а вместо dx и dy — дифференциалы этих функций dx = х'(t)dt и dy = y'(t)dt. Тогда интегралы в правой части (1.3) сведутся к двум интегралам от функций действительного переменного t по отрезку (α, β) :
β |
|
β |
|
′ |
′ |
′ |
|
∫(u(z(t))x (t) −v(z(t)) y (t))dt +i∫(v(z(t))x (t) + |
|
||
α |
|
α |
|
|
|
′ |
(1.4) |
|
|
+u(z(t)) y (t))dt |
|
Это выражение легко преобразуется к виду
β |
|
β |
|
′ |
′ |
|
′ |
∫(u(z(t)) +iv(z(t)))(x (t) +iy (t))dt = ∫ |
f (z(t))z (t)dt |
||
α |
|
α |
|
Теперь мы готовы дать следующее определение.
Интегралом вдоль кривой Г от функции комплексного переменного f(z) называется число, обозначаемое ∫ f (z)dz и
вычисляемое по формуле |
|
Г |
β |
|
|
|
|
|
|
′ |
(1.5) |
∫ f (z)dz = ∫ f (z(t))z (t)dt |
||
Г |
α |
|
где z(t) = x(t) + iy(t), α ≤ t ≤ β , — уравнение кривой Г, a z'(t) =
= x'(t)+iy'(t).
Пример 1.1. Вычислить интеграл от функции f(z) = =(z - а)п по окружности радиуса r с центром а, направление обхода которой — против часовой стрелки.
Решение. Уравнение окружности z −a = r будет z −a = reit , или
z(t) = а + r(cost + i sint), 0 ≤ t ≤ 2π .
86
При изменении t от 0 до 2π точка z(t) движется по окружности Г против часовой стрелки. Тогда
f(z(t)) = (z(t) -а)п = rn(cost + i sint)n; z'(t) = r(— sint + i cost) = ir(cos t + i sint).
Применяя равенство (1.5) и формулу Муавра (2.12), получаем
∫(z −a)ndz = |
2∫π irn+1 (cos t +i sin t)n+1 dt = |
||
Г |
|
0 |
|
= irn+1 |
2∫π cos(n +1)tdt +i2rn+1 |
2∫π sin(n +1)tdt |
|
|
0 |
|
0 |
При n ≠ −1 оба последних интеграла равны нулю. При п = −1 имеем
∫ |
1 |
dz = i |
2∫π dt = i2π |
(1.6) |
|
z −a |
|||||
Γ |
|
0 |
|
Мы получили результат, важный для дальнейшего изложения:
|
∫ |
|
0 |
при |
n ≠ −1, |
(1.7) |
||
|
(z −a)n dz = |
|
|
|
||||
|
z−a |
|
=r |
2πi |
при |
n = −1. |
|
|
|
|
|
||||||
Заметим, что значение интеграла не зависит от радиуса r окружности.
Пример 1.2. Вычислить интеграл от функции f(z) = 1 по гладкой кривой Г с началом в точке а и концом в точке b.
Решение. Пусть кривая Г задается уравнением z(t) = =x(t)+ iy(t), α ≤ t ≤ β , причем а = z(α ), b = z( β ). Используя
формулу (1.5), а также формулу Ньютона-Лейбница для вычисления интегралов от действительных функций, получим
87
|
β |
β |
β |
||||
∫1dz = ∫z′(t)dt = ∫x′(t)dt +i∫y′(t)dt = x(t) |
|
αβ +iy(t) |
|
αβ = |
|||
|
|
||||||
Γ |
α |
α |
α |
||||
= x(β) − x(α) +i( y(β) − y(α)) = z(β) − z(α) = b −a |
|||||||
Мы видим, |
что интеграл |
∫1dz не зависит от вида пути Г, |
|||||
|
|
|
Γ |
||||
соединяющего точки а и b, а зависит только от концевых точек.
Изложим вкратце другой подход к определению интеграла от комплексной функции f(z) по кривой, аналогичный определению интеграла от действительной функции по отрезку.
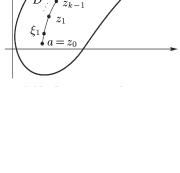
Разобьем кривую Г произвольным образом на п участков
точками z0 = a, |
z1, |
…, zn−1, |
zn = b, занумерованными в |
|
||||
|
|
|
|
направлении движения от |
|
|||
|
|
|
начальной точки к конечной (рис. |
|||||
|
|
|
|
5.1). Обозначим z1 − z0 = |
|
|||
|
|
|
= |
z1,..., zk |
− zk −1 = |
zk , zn − zn−1 = |
zn |
|
|
|
|
(Число |
zk изображается векто- |
||||
|
|
|
ром, идущим из точки zk −1 в zk .) |
|||||
|
|
|
|
На каждом участке ( zk −1, zk ) |
|
|||
|
Рис. 5.1 |
кривой выберем произвольную |
||||||
|
|
точку ζk и составим сумму |
|
|||||
|
|
|
|
|
n |
|
|
|
f (ζ1 ) z1 + f (ζ2 ) z2 +... + f (ζn ) |
zn = ∑ f (ζk ) |
zk |
|
|||||
|
|
|
|
|
k =1 |
|
|
|
Эта |
сумма |
|
называется |
интегральной |
суммой. |
|||
Обозначим |
через |
λ |
длину |
наибольшего |
из участков, |
на |
||
которые разбита кривая Г. Рассмотрим последовательность разбиений, для которой λ → 0 (при этом n → ∞).
88
Предел интегральных сумм, вычисленный при условии, что длина наибольшего из участков разбиения стремится к нулю, называется интеграломот функции f(z) по кривой Г и
обозначается ∫ f (z)dz :
Γ
|
n |
|
∫ f (z)dz = limλ→0 |
∑ f (ζk ) zk |
(1.8) |
Γ |
k =1 |
|
Можно показать, что это определение также приводит нас к формуле (1.3) и, следовательно, эквивалентно определению (1.5), данному выше.
Установим основные свойства интеграла ∫ f (z)dz .
Γ
1°. Линейность. Длялюбыхкомплексныхпостоянныхаиb
∫(af (z) +bg(z))dz = a∫ f (z)dz +b∫g(z)dz
Γ Γ Γ
Это свойство следует из равенства (1.5) и соответствующих свойств интеграла по отрезку.
2°. Аддитивность. Если кривая Г разбита на участки Г1 и Г2, то
∫ f (z)dz = ∫ f (z)dz + ∫ f (z)dz
ΓΓ1 Γ2
Доказательство. Пусть кривая Г с концами а, b разбита точкой с на две части: кривую Г1 с концами а, с и кривую Г2 с концами с, b. Пусть Г задается уравнением z = z(t), α ≤ t ≤ β , причем а = z(α ), b = z( β ), с = z(γ) . Тогда
уравнения кривых Г1 и Г2 будут z = z(t), где α ≤ t ≤γ |
для Г1 и |
|
γ ≤ t ≤ β |
для Г2. Применяя определение |
(1.5) и |
соответствующие свойства интеграла по отрезку, получим
89
|
β |
γ |
β |
|
∫ f (z)dz = ∫ |
′ |
′ |
′ |
|
f (z(t))z (t)dt = ∫ |
f (z(t))z (t)dt + ∫ |
f (z(t))z (t)dt = |
||
Γ |
α |
α |
γ |
|
|
|
|
= ∫ f (z)dz + ∫ f (z)dz , |
|
|
|
|
Γ1 |
Γ2 |
что и требовалось доказать.
Свойство 2° позволяет вычислять интегралы не только по гладким кривым, но также и по кусочно гладким, т.е. кривым, которые можно разбить на конечное число гладких участков.
3°. При изменении направления обхода кривой интеграл меняет знак.
Доказательство. Пусть кривая Г с концами а и b задается уравнением z = z(t), α ≤ t ≤ β . Кривую, состоящую из
тех же точек, что и Г, но отличающуюся от Г направлением обхода (ориентацией), обозначим через Г-. Тогда Г- задается уравнением z = z1(t), где z1(t) = z(α + β −t ),α ≤ t ≤ β . Действительно, введем новое переменное τ =α + β −t . При из-
менении t от α до β |
переменное τ |
изменяется от β до α . |
|||
Следовательно, точка z(τ) пробежит кривую Г-. |
|
||||
Легко |
видеть, |
что |
z1′(t) = zτ′(τ)(α + β −t)′t = −zτ′(τ) , |
||
dt = −dτ . |
Используя |
определение |
(1.5) и |
переходя к |
|
переменному τ , получим
ββ
∫f (z)dz = ∫ f (z1 (t))z1′(t)dt = ∫ f (z(τ))(−zτ′(τ))(−dτ) =
Γ− |
α |
α |
β
|
′ |
= −∫ f (z(τ))z (τ)dτ = −∫ f (z)dz . |
|
α |
Γ |
Свойство 3° доказано. (Заметим, что из определения интеграла (1.8) это свойство следует непосредственно: при изменении ориентации кривой все приращения zk меняют знак.)
90
