точку ω0 , лежащую выше прямой y =1 4 , то приходим к выводу: круг z + 2i < 2 отображается на полуплоскость
4 , то приходим к выводу: круг z + 2i < 2 отображается на полуплоскость
Im z >1 4 .
4 .
Образ границы z + 2i = 2 можно было найти и другим способом, показанным на следующем примере.
Задача 8.15. В какую область переходит круг z +i < 3
при отображении ω =1 z ? |
|
Решение. Найдем образ окружности |
z +i = 3. |
Поскольку z = 0 не принадлежит этой окружности, то ни одна из ее точек не перейдет в ω = ∞. Значит, образом будет окружность конечного радиуса. Для отыскания ее центра и
|
|
|
|
|
|
|
|
|
|
|
|
радиуса |
положим |
z = x +i y , |
|
ω = u +i υ и представим |
уравнение |
|
z +i |
|
= 3 в виде |
|
2 |
= 9 , x 2 + y 2 + 2 y −8 = 0 . |
|
|
|
|
x +i u +1 |
|
|
= 3 |
, или |
x 2 + |
y +1 |
|
|
|
|
( |
) |
|
|
|
( |
) |
|
Равенство ω =1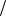 z дает z =1
z дает z =1 ω , или
ω , или
1u −i υ
x+i y = u +i υ = u 2 +υ2 ,
Подставим эти выражения в уравнение окружности:
1 |
|
2 υ |
−8 = 0 , 8(u |
2 |
2 |
)+ 2υ−1= 0 , |
|
+ |
|
|
+υ |
u 2 + υ2 |
u 2 + υ2 |
|
u 2 +υ2 + υ4 −18 = 0 .
Дополним выражение υ2 +υ 4 до полного квадрата:
4 до полного квадрата:
2 2 υ |
|
1 2 |
1 |
|
1 2 |
|
2 |
|
|
1 2 |
9 |
|
u +υ + + |
|
|
|
|
|
|
|
|
|
|
|
|
|
− − |
= 0 , |
|
υ+ |
= . |
4 |
|
|
8 |
|
|
|
|
|
|
|
64 |
|
|
8 |
|
8 |
|
|
|
|
8 |
|

Итак, |
окружность |
|
z +i |
|
|
= 3 |
переходит в |
окружность с |
|
|
центром ω0 = (0,−1 8) |
|
и |
|
|
радиусом |
R = 3 8 . |
Точка |
|
|
z → 0 , |
лежащая внутри круга |
|
z +i |
|
< 3 , |
переходит в точку |
ω = ∞. |
|
|
Значит, при отображении ω =1 z |
круг |
|
|
z +i |
|
< 3 переходит во |
|
|
внешность круга с центром ω0 = −i |
8 |
|
|
|
и радиусом |
|
R = 3 8 . |
Это множество можно задать неравенством ω0 +i 8 > 3 8 . |
|
Задача 8.16. Найти конформное отображение |
ω = f (z) |
круга |
|
z |
|
<1 |
на круг |
|
|
|
ω |
|
<1 , |
удовлетворяющее |
условиям |
|
|
|
|
|
ω(−i |
2)= 0 , |
arg ω′(−i 2)= π 4 . |
Указать |
коэффициент |
растяжения в точке z0 = −i 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. В примере 4.8 было показано, что дробно- |
линейная функция, отображающая круг |
|
z |
|
<1 на круг |
|
ω |
|
<1 , |
|
|
|
|
имеет вид (формула (4.10)): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = eiϕ |
|
z −z0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−z0 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
где z0 — точка, переходящая в точку ω = 0 . В нашем случае z0 = −i 2 . Осталось определить значение ϕ, которое найдем из условия arg ω′(−i
2 . Осталось определить значение ϕ, которое найдем из условия arg ω′(−i 2)= π
2)= π 4 :
4 :
|
iϕ |
|
( |
|
|
0 |
) |
( |
|
|
|
|
|
|
0 )( |
z −z |
0 ) |
|
|
|
|
iϕ |
|
|
|
0 |
z |
|
|
ω′(z)= e |
|
1 1−z |
z |
− −z |
|
|
|
|
|
|
|
= e |
|
|
|
|
1−z |
|
|
. |
|
|
|
|
|
|
|
|
1−z |
z |
) |
2 |
|
|
|
|
|
|
|
|
1−z |
z |
) |
2 |
|
|
|
|
|
|
|
( |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
0 |
|
|
|
|
Учитывая, что z z0 = |
|
z0 |
|
|
2 , при z0 |
= −i |
2 |
|
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
ω′(z |
0 )= e |
iϕ |
1− |
|
z0 |
|
|
2 |
|
|
= e |
iϕ |
1 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1− |
|
z0 |
|
2 ) |
2 |
|
1− |
|
z0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
iϕ |
1 |
|
4 |
|
iϕ |
|
|
|
|
|
= e |
|
|
= |
|
e . |
ω′ |
− |
|
|
|
|
|
|
|
|
|
|
|
1−1 4 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Отсюда следует, что |
|
) |
|
|
|
|
|
( |
|
|
|
) |
|
( |
|
= 4 3 , |
|
|
|
2 |
= ϕ. |
ω′ −i 2 |
|
arg ω′ −i |
|
Значит, коэффициент растяжения в точке −i 2 равен 4
2 равен 4 3 , и ϕ= π
3 , и ϕ= π 4 . Искомым отображением является функция
4 . Искомым отображением является функция
ω = ei π 4 |
z +i 2 |
= ei π 4 |
z +i 2 |
|
|
|
1−i 2 z |
1+i z 2 |
(мы использовали равенство i = −i ).
Задача 8.17. Найти конформное отображение верхней полуплоскости Im z > 0 на круг ω <1 , удовлетворяющее
условиям ω(2i)= 0 , arg ω′(2i)= π. Указать коэффициент растяжения в точке z0 = 2i .
Решение. В примере 4.7 было показано, что конформное отображение верхней полуплоскости на единичный круг имеет вид
ω = eiϕ z −z0 . z −z0
Определим параметры z0 и ϕ. Поскольку z0 — точка, переходящая в точку ω = 0 , то z0 = 2i . Для определения ϕ найдем ω′(z0 ):
ω′(z)= e |
iϕ 1 (z −z |
0 )−1 (z −z0 ) |
= e |
iϕ z0 −z0 |
|
, |
|
|
|
|
|
|
|
|
|
(z −z0 ) |
2 |
|
(z −z0 ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
ω′(z |
0 )= e |
iϕ |
|
|
z0 −z0 |
|
= e |
iϕ |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
(z0 −z0 ) |
2 |
|
|
z0 |
−z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω′(2i)= |
eiϕ |
|
eiϕ |
|
|
|
i eiϕ |
|
1 |
|
iπ |
|
|
i π |
2 |
|
iϕ |
|
|
1 |
|
i(3π 2+ϕ) |
|
|
|
= 4i = − |
4 = |
4 e |
|
e |
|
|
e |
|
= |
4 e |
|
|
2i + 2i |
|
|
|
|
|
|
(мы использовали равенства −1= ei π , i = ei π 2 ). Отсюда |
|
|
|
ω′(2i) |
|
1 |
, arg ω |
′(2i)= |
3π |
|
|
|
|
|
= |
|
3π |
+ϕ, |
ϕ |
= − |
π |
|
|
|
|
|
|
|
|
|
|
|
= 4 |
|
2 +ϕ , т.е. π |
|
2 |
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, искомое отображение дается функцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−iπ 2 z −2i |
|
|
z −2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = e |
|
|
|
|
= −i |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z + 2i |
z + 2i |
|
|
|
|
|
|
|
Коэффициент растяжения в точке 2i равен ω′(2i) =1 4 .
Задача 8.18. Найти конформное отображение полосы, заключенной между прямыми y = x +1 и y = x +3 (рис. 8.7),
на единичный круг.
Решение. 1) С помощью линейной функции ω = a z +b
отобразим |
данную полосу на полосу −∞< x < +∞, |
0 < y < π. |
Исходная |
полоса имеет ширину 2 . Чтобы отобразить ее на полосу шириной π, сделаем преобразование подобия с
|
коэффициентом |
π |
2 . |
Это |
|
преобразование задается функцией |
|
ω1 = π z 2 . Точка |
A(−1 2, i 2) |
|
перейдет |
|
) |
в |
|
( |
|
|
Рис. 8.7 |
A1 −π (2 2), π |
(2 2) . |
|
|
|
|
|
Затем повернем полученную полосу на угол π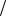 4 по
4 по
часовой стрелке, чтобы она стала параллельной оси OX . Это преобразование запишется в виде
ω2 = ω1e−i π 4 = π2z e−i π 4 .
Точка A1 (−π (2 2), π
(2 2), π (2 2)) перейдет в A2 (0, π
(2 2)) перейдет в A2 (0, π 2).
2).
Наконец, сделаем параллельный перенос на вектор A2O :
ω3 = ω2 −i2π = π2z e−i π 4 −i2π .
Вместо точки A(−1 2, i
2, i 2) можно было взять любую другую точку на прямой y = x +1 (например, точку (0,1) ). Используя
2) можно было взять любую другую точку на прямой y = x +1 (например, точку (0,1) ). Используя
равенство e−i π 4 =1 |
2 −i |
2 можно записать полученное |
преобразование в такой форме: |
|
|
|
|
π 1−i |
) |
|
ω |
3 = |
|
( |
z −i π . |
|
2 |
|
|
|
|
2 |
2)Отобразим полученную полосу на верхнюю
полуплоскость |
Im z > 0 . |
Было показано, что показательная |
функция ω =e z |
отображает полосу 0 < Im z < π на верхнюю |
полуплоскость. |
Поэтому |
нужным преобразованием будет |
ω4 =e ω3 . |
|
|
3)Отобразим верхнюю полуплоскость на единичный
|
круг |
с |
|
помощью |
дробно-линейного |
отображения |
|
ω = eiϕ |
z −z |
0 |
, Im z0 > 0 . Поскольку никаких дополнительных |
|
z −z |
0 |
|
|
|
|
|
условий не задано, то параметры ϕ и z0 с Im z0 > 0 можно
выбрать произвольно. Например, возьмем ϕ0 = 0 , z0 = i .
Тогда получим ω = ω4 −i .
ω4 +i
4) Искомое отображение будет композицией указанных выше отображений:
|
|
|
|
|
|
|
|
|
|
π 1−i |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
iπ |
|
|
|
|
|
|
|
|
ω3 |
|
|
exp |
|
|
− |
|
−i |
|
|
|
|
|
|
|
|
|
|
|
|
ω4 −i |
|
e |
|
−i |
|
|
2 |
|
|
2 |
|
|
|
ω = |
= |
|
= |
|
|
|
|
|
. |
ω |
4 |
+i |
e |
ω3 |
+i |
|
π 1−i |
) |
|
|
|
|
|
|
|
|
|
|
( |
|
iπ |
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
− |
|
|
+i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 8.19. Найти все значения степени (− 3 +i)−6i .
Решение. Согласно определению общей степенной функции
(− 3 +i)−6i = e−6i Ln(− 3+i) .
Значения логарифма найдем по формуле:
|
Ln(− 3 +i)= Ln |
|
− 3 +i |
|
+i(arg(− 3 +i)+ 2πk); |
|
|
|
|
|
− 3 +i |
|
= (− 3)2 +1 = 2 ; cosϕ= − |
3 |
, sin ϕ= |
1 |
, |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
где ϕ= arg(− 3 +i). Поэтому ϕ лежит во второй четверти. Следовательно, ϕ= 5π 6 . Получаем
6 . Получаем
(− 3 +i)−6t =
= exp −6i ln 2 +i 56π + 2πk = exp(5π+12πk −i6 ln 2)=
( |
) |
= exp(5π+12πk) cos(6ln 2)−i sin(6ln 2) , k ]. |
Мы получили, что данная степень |
(− 3 +i)−6i имеет |
бесконечное множество значений. Все эти значения лежат на одном луче, идущем под углом θ = −6 ln 2 к оси OX . Модули этих значений образуют две геометрические прогрессии с
первым членом |
b = e5π |
и знаменателями q = e12π |
при |
|
1 |
|
|
k =1, 2,3,... , и q = e−12π при k = −1,−2,−3,...
Задача 8.20. Найти все значения функции
Arc cos(−5i).
Решение. По формуле (4.3)
Arc cos(−5i)= i Ln(−5i + (−5i)2 −1)= i Ln(−5i + −26)=
( |
) |
= i Ln(−5i ±i 26)= i Ln i(−5i ± 26) . |
Мы пишем ± перед 26 , поскольку под корнем |
из |
положительного числа обычно понимается арифметическое значение корня, в то время как под корнем в формуле (4.3) подразумевается двузначная функция. Рассмотрим каждый из знаков перед корнем отдельно:
|
i(−5i + 26) |
|
= 26 −5 =( 26 +5)−1 |
|
( |
|
) |
|
|
, |
arg i(−5 + |
6) = π 2 |
(мы воспользовались равенством ( |
26 −5)( |
26 +5)=1). По |
формуле (4.5) |
|
|
|
|
( |
|
|
|
) |
|
|
|
|
|
+ 2πk)= |
|
i Ln i(−5 |
+ 26) |
= i ln( 26 −5)−(π 2 |
|
|
|
|
|
|
|
|
|
= −i ln( 26 +5)−(π 2 + 2πk), k ]. |
Аналогично, |
|
|
|
|
|
|
|
|
|
|
|
|
|
i(−5− 26) |
|
|
|
|
( |
|
|
|
) |
|
|
= |
26 +5 , |
arg −i( |
26 +5) |
= −π 2 , |
( |
|
( |
|
) |
|
|
( |
|
) |
|
|
|
|
|
|
i Ln −i |
|
) |
|
|
|
( |
2 + |
2πk |
) |
= |
|
26 +5 = i ln 26 +5 − −π |
|
|
|
|
|
|
|
|
|
= i ln( 26 +5)+(π 2 + 2πk), k ]. |
Мы пишем +2πk вместо −2πk , поскольку k |
пробегает все |
множество целых чисел. Окончательно получаем |
|
|
|
|
|
( |
|
|
|
( |
|
) |
|
|
|
|
|
( |
) |
|
|
|
|
|
|
) |
, k = 0,±1,±2,... |
Arc cos −5i |
= ± π 2 |
+ 2πk +i ln 26 +5 |
|
Можно было рассмотреть только один случай и воспользоваться общим замечанием, сделанным в п.4.3, согласно которому изменение знака перед корнем приводит к
изменению знака перед логарифмом Ln(z + |
z 2 +1). |
|
Задача |
8.21. |
Найти |
все |
значения |
функции |
Arctg −2 3 +3i . |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Решение. По формуле (4.4) при z = (−2 |
3 +3i) |
3 имеем |
|
Arctg z = |
1 |
Ln |
i −z |
= |
1 |
Ln |
|
2 3 |
|
; |
|
2i |
i + z |
2i |
−2 3 + 6i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
= |
|
|
1 |
|
|
= |
−1−i 3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 3 + 6i |
|
−1+i 3 |
4 |
|
|
|
|
|
|
|
|
|
−1−i 3 |
|
= |
1 |
|
|
|
3 |
|
; |
|
arg −1−i |
3 = ϕ= −2π . |
|
|
|
|
|
|
|
|
|
|
= 1 |
|
|
|
|
|
|
|
1+i |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равенство |
для |
|
|
|
ϕследует |
из |
того, |
что |
sin ϕ= − 3 |
2 , |
cosϕ= −1 2 . Отсюда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 3 +3i |
|
|
|
|
1 1 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arctg |
|
|
|
|
|
|
= |
|
|
|
ln |
|
+i − |
|
+ 2πn = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −π |
+ πn + |
|
1 |
|
|
|
ln |
1 |
= − |
π + πn + |
i |
ln 2 , |
n = 0,±1,±2,... |
|
|
|
2i |
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
Интегрирование функций комплексного |
|
|
|
|
|
переменного. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 8.22. Вычислить интеграл от функции |
f (z)= z 2 |
по |
кривой |
Γ, |
|
являющейся |
ломаной |
ABC , |
где |
( |
|
) |
, |
|
A −1, 0 |
|
( |
) |
( |
|
) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B 0,1 |
|
, C 1, 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. 1) Зададим кривую уравнением вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
( ) |
|
|
|
( ) |
, α≤t ≤β. |
|
|
|
|
|
|
|
|
|
|
|
z = z t |
|
|
|
= x t |
+i y t |
|
|
|
|
|
Поскольку кривая состоит из двух участков — отрезков AB и BC , задаваемых разными уравнениями, то рассмотрим каждый из них отдельно.
|
Участок |
AB |
можно |
задать |
уравнением |
y = x +1, |
−1≤ x ≤0 |
или, |
в параметрической |
форме, |
( ) |
= t , |
x t |
( ) |
|
|
( ) |
( |
|
) |
|
|
|
|
|
y t |
= t +1, т.е. z t |
= t +i t |
+1 , −1≤t ≤0 . |
|
|
|
|
Участок |
BC задается уравнением y = −x +1, |
0 ≤ x ≤1. |
Параметрическими |
уравнениями |
отрезка |
BC |
являются |
( ) |
( ) |
|
|
( ) |
|
( |
) |
, 0 ≤t ≤1 . |
|
x t |
= t , y |
t |
= −t +1, или z t |
= t +i −t +1 |
|
2) Найдем интеграл по кривой Γ по формуле
β
∫ f (z)dz = ∫ f (z(t))z′(t)dt .
Γα
Для этого перейдем к сумме интегралов по участкам AB и BC и вычислим каждый из них в отдельности.
Для участка AB
|
|
|
|
|
|
|
|
|
|
( ) |
=1+i ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z′ |
t |
|
|
|
|
|
|
|
∫ |
|
∫( |
|
|
|
|
) |
2 dz = |
0 |
|
|
|
|
|
|
2 |
z′ t |
|
|
|
|
|
|
z 2dz = |
x |
−i y |
|
t −i t +1 |
dt = |
|
|
|
|
|
|
|
|
∫( |
( |
|
)) |
|
|
|
( ) |
|
|
|
|
|
|
Γ1 |
|
Γ1 |
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
−2it t +1 − t +1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
t 2 |
|
|
1+i |
|
dt = |
|
|
|
|
|
|
|
∫( |
|
( |
|
) |
( |
|
) )( |
) |
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
( |
2t 2 −1+i(−2t 2 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
−4t −1) dt |
= |
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t 2 |
|
|
2t |
3 |
|
|
|
2 |
|
|
0 |
|
|
|
1 i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−t |
|
|
|
−2t |
|
|
|
|
= − |
|
+ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
= |
3 |
+i − |
3 |
|
|
−t |
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для участка BC
z′(t) =1−i ;


 4 , то приходим к выводу: круг z + 2i < 2 отображается на полуплоскость
4 , то приходим к выводу: круг z + 2i < 2 отображается на полуплоскость 4 .
4 . z дает z =1
z дает z =1 ω , или
ω , или 4 до полного квадрата:
4 до полного квадрата:
 2 . Осталось определить значение ϕ, которое найдем из условия arg ω′(−i
2 . Осталось определить значение ϕ, которое найдем из условия arg ω′(−i 2)= π
2)= π 4 :
4 :







 2 равен 4
2 равен 4 3 , и
3 , и  4 . Искомым отображением является функция
4 . Искомым отображением является функция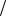 4 по
4 по

 2
2 2,
2,  2
2 6 . Получаем
6 . Получаем