Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1865

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

(

)

приращение

функции

)

равно

ϕ= ϕ (ω0 )−arg ω0 =

Γ arg f . Таким образом,

ΔΦ(z)= i

Γ arg f .

Из этого равенства, а также из (7.30) и (7.26) получаем

∫

f ′(z)

Γ arg

f =

ΔΦ(z)=

dz =

2πi(N −P)= 2π(N −P),

f (z)

что и требовалось доказать.

Пусть, например, Γ — достаточно малая окружность,

охватывающая

нуль кратности

функции

f (z). Тогда

N = n ,

P = 0 . Согласно теореме 4.3, при однократном обходе

точкой

z окружности

Γ вектор

f (z) совершит

n оборотов

вокруг начала координат против часовой стрелки. Если же Γ охватывает полюс порядка p (т.е. N = 0 , P = p ), то вектор

f (z) совершит p оборотов по часовой стрелке.

Полезным применением признака аргумента является следующая теорема.

Теорема 4.4 (теорема Руше). Пусть функции f (z) и g (z) аналитичны во всех точках замкнутого контура Γ и

внутри него и

f (z)

g (z)

на

Γ. Тогда

их

сумма

F (z)= f (z)+ g (z)

имеет внутри Γ

столько

же

нулей

учетом их кратности, что и f (z).

Доказательство. Покажем вначале, что функции

f (z)

F (z) не имеют нулей на Γ. Для любых комплексных чисел a и b справедливо неравенство a +b ≥ a − b . Оно следует из неравенства треугольника:

191

a = a +b−b ≤ a +b + −b = a +b + b , откуда

a +b ≥ a − b .

Используя это неравенство и условие теоремы, получим

f (z) > g (z) ≥0 , F (z) = f (z)+ g (z) ≥ f (z) − g (z) > 0

для всех z Γ. Значит, f (z) и F (z) не обращаются в нуль на Γ, и кним можно применить принцип аргумента. Так как f (z)≠0 на Γ, то

f (z)+ g (z)= f (z) 1+ g (z) .f (z)

При умножении комплексных чисел их аргументы складываются. Отсюда следует, что

Γ arg( f + g)=

Γ arg f +

Γ arg 1

По

условию

теоремы,

g (z)

<1 для

всех

точек

z Γ.

Поэтому

если

f (z)

обозначить

ω(z)=1+

g (z)

то

ω−1

g (z)

Это

<1.

f (z)

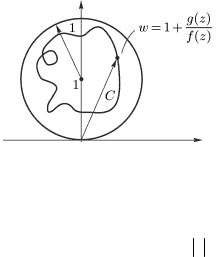
неравенство обозначает, что при обходе точкой z контура Γ точка ω будет двигаться по замкнутой территории, лежащей

внутри круга ω−1 <1 (рис. 7.5). Следовательно, вектор ω не сделает ни одного оборота вокруг точки ω = 0 ; аргумент ϕ(ω) числа ω вернется к начальному значению, и его

приращение	Γ	(	f	)	будет	равно	0 . Итак,
		arg 1+ g
Γ arg( f + g)=		Γ arg f . Применяя к				каждой	из функций
f + g и f равенство (29.3)			с		P = 0

192

(функции аналитичны, и полюсов нет), приходим к тому, что эти функции имеют внутри Γ одинаковое число нулей. Теорема Руше доказана.

Теорема				4.4	иногда
позволяет определить число
нулей	функции			в	заданной
области.
Пример 4.5. Определить
число	корней			уравнения
z8 −4z5 + z2 −1= 0 в круге
Рис. 7.5		z	<1.

Решение. Возьмем f (z)= −4z5 , g (z)= z8 + z2 −1.

В точках окружности z =1 имеем

g (z)

f (z)

−4z5

= 4 ,

z8 + z2 −1

≤

−1

= 3

Таким образом,

f (z)

g (z)

на окружности Γ= {

=1}. По

теореме Руше функция

f (z)+ g (z)= z8 −4z5 + z2 −1 имеет в

круге

столько

же

нулей,

сколько и

функция

f (z)= −4z5 . Но f (z)

обращается

в нуль только

в точке

z = 0 ,

являющейся нулем

функции

f (z) пятого

порядка.

Следовательно,

и функция

f (z)+ g (z) имеет в круге

пять нулей (с учетом кратности).

Важным применением теоремы Руше является простое доказательство с ее помощью так называемой основной теоремы алгебры.

193

Теорема 4.6 (основная теорема алгебры). Любой многочлен

п-й степени

Pn (z)= a0 zn + a1zn−1 +...+ an ,

a0 ≠0 ,

имеет

плоскости

С комплексного переменного

точности

нулей с учетом их кратности.

Доказательство. Запишем Pn (z)

в видеPn (z)= f (z)+ g (z),

где f (z) = a0 zn ,

g (z) = a1zn−1 +...+ an . Так как

lim

f (z)

= lim

a0 zn

= lim

= ∞,

z→∞ g (z)

z→∞ a1zn−1 +...+ an

z→∞ a1

z +...

+ zn

то найдется такое число R0 > 0 , что при

≥ R0 будет

f (z)

≥2

g (z)

Возьмем

произвольное R > R0 .

Тогда

при

= R

получим

f (z)

≥2

g (z)

По

теореме

Руше Pn (z)

имеет в круге

< R столько же нулей,

сколько и функция

f (z) = a0 zn .

Эта функция имеет нуль кратности n

в начале

координат, т.е.,

с учетом кратности, n нулей. Таким образом,

в любом круге

< R сколь угодно большого радиуса R > R0

многочлен Pn (z) имеет ровно n нулей. Значит, и во всей комплексной плоскости ^ их будет в точности n .

194

8. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Комплексные числа и действия над ними.

Задача 8.1. Число ( 3 −i)7 представить в алгебраической форме.

Решение. Напомним, что алгебраической (декартовой) формой комплексного числа называется выражение z = x +iy .

1) Представим число z = 3 −i в тригонометрической форме. Для этого найдем модуль r и аргумент ϕ этого числа:

r =

(

)

(

)

2 = 3+1 = 2 ;

+ −1

cosϕ=

;

sin ϕ=

= −1 ,

откуда

следует, что

лежит

в 4-й четверти. Поэтому

ϕ= −

+ 2πk , k ]. Можно взять любое из этих значений

ϕ. Итак,

3−i = 2 cos −π6 +i sin −π6 .

2)По формуле Муавра (2.10) найдём z 7 :

7		7		7π					7π
( 3 −i) = 2
							+i sin					=
			cos −				+i sin		−			=

						6			6
					π			π				3		1	(	)
		7			π	+i sin		π		7		3	+i	1			.
	= 2								= 2		−
	= 2		−cos		6			6	= 2		−	2		2	= 64 −	3 +i
					6			6				2		2

195

Задача 8.2. Найти все значения корня												4 −1−i		3
												2
Решение.				1)	Найдем			модуль и				аргумент				числа
z = −1 −i	3	стоящего под знаком корня:
z = −1 −i	2	стоящего под знаком корня:
2	2
				2		3	2	1		3					1
			1			3		1		3					1
r =	−			+−			=		+		=1; cosϕ= −					;
r =	−		2	+−		2	=	4	+	4	=1; cosϕ= −				2	;
			2			2		4		4					2

						sin ϕ= −			3	.
						sin ϕ= −			2	.
									2
Следовательно, ϕ лежит в 3-й четверти, и ϕ= −													2π	+ 2πk ,
Следовательно, ϕ лежит в 3-й четверти, и ϕ= −														+ 2πk ,
												3

k].

2)Применим формулу (1.12); в качестве ϕ можно взять любое из найденных значений, например ϕ= −23π . Получим

							2π									2π
						− + 2πk									− +
	−1−i 3					− + 2πk									− +				2πk
	−1−i 3						3									3
4			4				3									3
		=		1	cos								+i sin								=
	2								4									4
	2								4									4



								π			π						π		π
								π		+	π	k					π	+	π
				= cos −						+		k		+i sin −				+		k , k = 0,1, 2,3.
								6			2						6		2
								6			2						6		2

Подставляя каждое из указанных значений fc, найдем искомые значения корня:

						3		1
ω0		π		π	=	3	−i	1	;
ω0	= cos −		+i sin −		=		−i		;
						2		2
		6		6		2		2

196

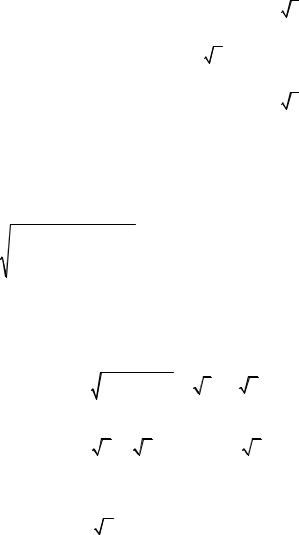
	ω1		= cos			π +i sin π								=	1	+i		3
	ω1		= cos			π +i sin π								=	2	+i		2
					3			3							2			2
	ω2		= cos			5π		+i sin		5π			= −		3	+i		1
	ω2		= cos		6			+i sin		6					2	+i		2
					6					6					2			2
	ω3		= cos			4π		+i sin		4π				= −1		−i		3
	ω3		= cos		3			+i sin		3				= −1		−i		2
					3					3					2			2
Другие значения k новых чисел ωk														уже не дадут.
Задача 8.3. Выполнить действия над комплексными
числами: 3		(2−2i)4 + 72 + 4i								. Изобразить найденные числа на
			1−2i		)		2 +5i
			(		)
комплексной плоскости.
Решение. 1) Число (2−2i), которое возводится в степень
4 , представим в тригонометрической форме:
			r =	z		= 2 2 + −2						)	2	= 8 = 2 2 ;
			r =	z		= 2 2 + −2							2	= 8 = 2 2 ;
										(
			cosϕ=					2	=	1	,			sin ϕ= −		1	.
			cosϕ=					2	=	2	,			sin ϕ= −		2	.
							2	2		2						2

следовательно ϕ, лежит в 4-й четверти, и ϕ= −π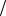4 . Отсюда

		π		π
2−2i = 2 2
2−2i = 2 2	cos −		+i sin −	.

		4		4

2) Выполним действия возведения в степень. Степень (2−2i)4 найдем по формуле Муавра:

197

(2−2i)4 = (2 2)4 cos −44π +i sin −44π =

= 64(−1+i0)= −64 .

Для нахождения (1 — 2i)2 удобнее применить алгебраическую формулу сокращенного умножения:

(1−2i)2 =1−4i +(2i)2 =1−4i −4 = −3−4i .

3) Выполним сложение чисел в алгебраической форме:

(2−2i)4 + 72 + 4i = −64 +72 + 4i = 8 + 4i ;

(1−2i)2 +5i = −3−4i +5i = −3+i .

4) Выполним деление чисел в алгебраической форме. Для этого домножим числитель и знаменатель дроби на число, сопряженное знаменателю:

	8 + 4i		(		)(		)					−24−12i −8i + 4
		=	8		+ 4i −3−i				=											=
	−3+i	=		(−3+i)(−3−i)					=				−3				2	+1		=
													(			)
																		=	−20−20i				= −2−2i .
																				10
5)			Извлечем			кубический								корень,					применив				формулу
Муавра.					Вначале			представим										число			(		−2i	)	в
Муавра.					Вначале			представим										число			−2		−2i		в
тригонометрической форме:
					r = −2						)	2	+ −2		)	2	= 8 = 2 2 ;
						(					)		(		)
					cosϕ= −					2			= −	1			;	sin ϕ= −			1	,
					cosϕ= −							2	= −		2		;	sin ϕ= −			2	,
							2					2			2						2

198

следовательно, ϕ лежит в 3-й четверти, и ϕ= −3π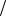4 (можно взять ϕ= 5π4 );

−2−2i = 2 2 cos −34π +i sin −34π .

По формуле (1.12)

−3π

+ 2πk

−3π + 2πk

−2−2 i =

2 2

cos

+i sin

k = 0,1, 2 .

Так как 3 2

2 =

2 , то при k = 0

ω0 =

cos

−

+i sin

=1−i ;

при

−

k =1

5π

ω1 =

cos

+i sin

;

при k = 2

13π

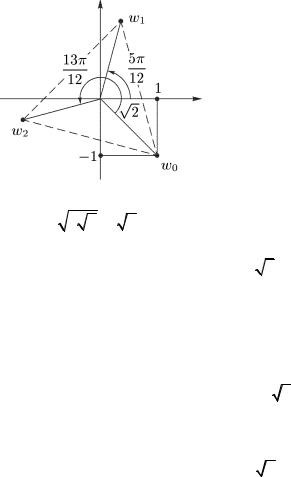
Рис. 8.1

ω2 =

cos

+i sin

6) Изобразим найденные числа на комплексной

плоскости

(рис.

8.1).

Точки

ω0 ,

ω1 ,

ω2

расположены в

вершинах правильного треугольника с центром в начале координат.

199

Задача 8.4. Найти все решения уравнения z 6 + 28 z 3 +

+27 = 0 .

Решение. По основной теореме алгебры уравнение имеет шесть корней (возможно, среди них есть совпадающие).

Сделаем

замену

переменного

t = z 3 :

t 2 + 28t + 27 = 0 ;

дискриминант D = 28 2 −4 27 = 676 = 26 2 ;

корни

t1 = −27 ,

t2 = −1.

Найдем значения z . При t1 = −27 имеем z 3 = −27 . Для

аргумента ϕ числа −27 получаем

cosϕ= −1,

sin ϕ= 0 .

Поэтому ϕ= π, и t1 = −27 = 27(cos π+i sin π).

По формуле

(1.12)

z = 3 t1

π+ 2πk

+i sin

π+ 2πk

k = 0,1, 2.

27 cos

Отсюда

при

k = 0

z1 =

cos

+i sin

;

при

k =1

z 2 = 3(cos π+i sin π)= −3 ;

5π

при

k = 2

cos

+i sin

−i

;

Для t2 = −1 будет r =1, ϕ= π. Аналогично получаем

+i sin

z5 = −1;

z6 =

−i

=1 cos

;

Итак, все корни уравнения оказались различными.

200

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20222.52 Mб3Учебное пособие 1860.pdf
#
30.04.20222.52 Mб5Учебное пособие 1861.pdf
#
30.04.20222.54 Mб2Учебное пособие 1862.pdf
#
30.04.20222.54 Mб3Учебное пособие 1863.pdf
#
30.04.20222.54 Mб2Учебное пособие 1864.pdf
#
30.04.20222.54 Mб2Учебное пособие 1865.pdf
#
30.04.20222.54 Mб5Учебное пособие 1866.pdf
#
30.04.20222.55 Mб5Учебное пособие 1867.pdf
#
30.04.20222.55 Mб6Учебное пособие 1868.pdf
#
30.04.20222.56 Mб4Учебное пособие 1869.pdf
#
30.04.2022317.56 Кб6Учебное пособие 187.pdf