
Учебное пособие 1865
.pdf
|
Arg(z1z2 ) = Argz1 + Argz2. |
(2.6) |
||||||||||
Эти формулы означают, что вектор z1z2 |
получается из вектора |
|||||||||||
z1 поворотом на угол ϕ2 |
и умножением его длины на |
|
z2 |
|
. |
|||||||
|
|
|||||||||||
Например, |
умножение числа z на i |
дает вектор, |
который |
|||||||||
получается |
из вектора z |
поворотом |
на угол π / 2 |
против |
||||||||
часовой стрелки, так как i =π / 2 , |
|
i |
|
=1. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
Из формул (2.6) следует, что аналогичными свойствами обладает произведение любого конечного числа комплексных чисел. Например,
z1z2 z3 = (z1z2 ) z3 = z1z2 z3 = z1 z2 z3 ; Arg(z1z2 z3 ) = Arg((z1z2 ) z3 ) = Arg(z1z2 ) + Arg z3 =
= Arg z1 + Arg z2 + Arg z3.
В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = rn ; |
|
|
|
|
|
|
|
||||||||||||
|
|
zn |
|
|
= |
|
z z … z |
|
= |
|
z |
|
Arg(zn ) = nArg z. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n раз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zn |
= rn (cos |
nϕ +i sin nϕ). |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.7) |
|||||||||||||||||
Перейдем |
теперь |
к |
делению |
чисел |
z1 , z2 , заданных в |
||||||||||||||||||||||||||||||||
тригонометрической |
|
|
форме. |
|
|
Заметим, |
что |
если |
|||||||||||||||||||||||||||||
z2 = r2 (cos ϕ2 +i sin |
ϕ2 ) , |
|
то |
|
|
|
= r2 (cos |
|
(−ϕ2 ) +i sin |
(−ϕ2 )). |
|||||||||||||||||||||||||||
|
|
|
z2 |
|
|||||||||||||||||||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z1 |
|
|
|
z1 |
|
|
|
|
|
= |
r1r2 (cos (ϕ1 −ϕ2 ) +i sin |
(ϕ1 −ϕ2 )) |
, |
|
|||||||||||||||||||||
|
|
|
= |
|
z2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
z |
2 |
|
z |
2 |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
z1 |
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
= |
(cos (ϕ −ϕ |
2 |
) +i sin (ϕ −ϕ |
2 |
)). |
|
|
(2.8) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
z2 |
|
|
|
|
r2 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, модуль частного комплексных чисел равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя:
11

|
|
z |
|
= |
z1 |
|
, |
Arg |
z |
= Arg z − Arg z |
, |
если z |
|
≠ 0 . |
||||
|
|
1 |
|
|
|
1 |
2 |
|||||||||||
|
|
|
|
|||||||||||||||
|
|
z2 |
|
|
z2 |
|
|
|
|
z2 |
|
1 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В частности, если z1 =1 =1 (cos |
0 +i sin |
0) , |
|
|
||||||||||||||
z2 = zn = rn (cos |
nϕ +i sin |
nϕ) , то |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
z−n = |
1 |
|
(cos (−nϕ) +i sin |
(−nϕ)) |
|
(2.9) |
|||||
|
|
|
|
|
|
|
r2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положим по определению z0 |
=1 при |
z ≠ 0 . Тогда, в силу |
||||||||||||||||
формул |
(2.7) |
|
и |
(2.9), |
для |
любого |
|
целого |
|
числа m |
||||||||
(положительного, отрицательного или равного нулю) справедливо равенство, называемое формулой Муавра:
|
|
|
|
|
zm = rm (cos |
mϕ +i sin |
mϕ) . |
|
|
|
|
|
|
|
(2.10) |
|||||
|
|
Пример 2.4. Найти ( |
2 − |
6i)4 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решение. 1) Изобразим число |
|
2 − |
6i |
(см. рис. |
1.6) и |
|||||||||||||
запишем его в тригонометрической форме: |
|
|
|
|
|
|
|
|
||||||||||||
r = |
|
z |
|
= |
( 2)2 +(− 6)2 = |
2 +6 = |
8; |
cos ϕ = |
x |
|
= |
|
2 |
= |
1 , |
|||||
|
|
|||||||||||||||||||
|
|
r |
|
|
||||||||||||||||
|
|
|
|
|
ϕ = ±π +2πk, k |
|
|
|
|
|
|
|
|
|
|
8 |
|
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
откуда |
. |
Поскольку |
угол |
|
ϕ |
лежит |
в IV |
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
четверти (см. рис. 1.6), то |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ϕ = − |
π |
+2πk. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно |
взять главное |
|
значение |
аргумента |
|||||||||||
|
|
|
|
|
ϕ = −π . Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. z |
= |
8 |
|
|
π |
|
+i sin |
|
π |
|
|||||
|
|
|
|
|
cos |
− |
3 |
|
− |
. |
|
|||||||||
Рис. 1.6 |
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||
2) По формуле Муавра (2.10) найдем z4 :
12

|
4 |
|
|
4 |
|
|
|
4π |
|
|
4π |
|
|
|
|
|
|
|
2π |
|
2π |
||||
z |
|
= ( |
8) |
|
cos |
|
− |
|
+i sin |
|
− |
|
|
= 64 |
cos |
|
|
+i sin |
|
= |
|||||
|
|
3 |
3 |
3 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
64 |
|
− |
|
+ |
|
|
|
i |
= 32(−1 |
+ |
3i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(мы воспользовались тем, что |
− |
4π |
+2π = |
2π ). |
|
|
|
|
|
||||||||||||||||
|
|
5. |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Корнем |
степени n |
|
(n — |
|
натуральное число) |
из |
|||||||||||||||||
комплексного числа z называется такое комплексное число ω ,
n-я степень которого равна z, т.е. |
ωn = z . Корень n-й степени |
|||||||||||||
из z обозначается n z . |
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть z = r(cosϕ +i sinϕ) . Комплексное |
число |
ω = n z |
||||||||||||
будем |
искать |
в |
виде |
|
ω = ρ(cosθ +i sinθ) . |
Так |
как, по |
|||||||
определению, |
ωn |
= z , то |
|
ωn |
|
= |
|
z |
|
, |
Arg ωn = Arg z . Отсюда |
|||
|
|
|
|
|||||||||||
|
|
|
ρn = r, |
|
nθ =ϕ +2πk, k . |
|
(2.11) |
|||||||
Поскольку r |
и ρ — неотрицательные числа, то равенство |
|||||||||||||
ρn = r |
дает |
ρ = n r , |
|
причем |
берется арифметическое |
|||||||||
(неотрицательное) значение корня. Второе равенство в (2.11) дает
θ = |
ϕ +2πk , k = 0, ±1, ±2,… |
|
|
|
|||
Таким образом, |
n |
|
|
|
|
|
|
|
ϕ +2πk |
|
ϕ +2πk |
|
|
||
ω = n z = n |
|
+i sin |
, |
(2.12) |
|||
r cos |
n |
n |
|
||||
|
|
|
|
|
|
||
где k = 0, ±1, ±2,… Подставляя в (2.12) значения |
k = 0, ±1, ±2,… |
||||||
…, n −1, получим n различных значений корня n-й степени — числа ω0 ,ω1,…,ωn−1. Для каждого из них ωk = n r ; поэтому соответствующие им точки расположены на окружности
радиуса n r с центром в начале координат (рис. 1.7). Аргументы
13

θk = ϕ +n2πk = ϕn + 2nπ k
чисел ωk возрастают на 2π n при увеличении k на единицу.
n при увеличении k на единицу.
При k = n получим θn = ϕ |
+2π =θ0 +2π. Значит, точки |
ωn и |
|||
|
|
|
n |
|
|
ω0 совпадут. При |
k = n +1, n +2,…мы снова будем получать |
||||
точки ω1,ω2 . Аналогично, |
|
|
|||
при |
|
k = −1, −2,… |
|
|
|
соответствующие |
точки |
|
|
||
будут совпадать с какими- |
|
|
|||
то из точек ω0 ,ω1,…,ωn−1. |
|
|
|||
Мы |
приходим |
к |
|
|
|
следующему |
выводу. Для |
|
|
||
каждого |
комплексного |
|
|
||
числа |
z ≠ 0 |
имеется ровно |
|
|
|
n различных корней п-й степени из z. Все эти корни находятся по формуле (2.12)
при k = 0,1, 2,…, n −1. Соответствующие точки расположены
в вершинах правильного n-угольника с центром в начале координат.
Формула (2.12) также называется формулой Муавра.
Пример 2.5. Найти все значения 4 |
z при z = 32(−1+ 3 i) . |
|||||
Решение. Найдем модуль и аргумент числа z: |
||||||
r = |
322 ((−1)2 +( 3)2 ) = 32 2 = 64, |
|||||
cos ϕ = |
−32 |
= − 1 ; |
ϕ = ± |
2π |
+2πk, |
k . |
|
64 |
2 |
|
3 |
|
|
Так как Re z < 0, Im z > 0, то |
угол |
ϕ |
лежит |
во II четверти. |
||
Поэтому ϕ = 23π +2πk. В (2.12) можно взять любое значение
14

аргумента |
ϕ , |
|
в частности |
ϕ = |
2π |
. |
Подставляя |
найденные |
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значения r и ϕ в формулу (2.12), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
2π |
+2πk |
|
|
|
|
|
|
|
2π |
+2πk |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||
4 32(−1+ 3i) = 4 64 |
cos |
|
|
|
|
|
|
+i sin |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
π |
+ |
πk |
+i sin |
|
π |
+ |
πk |
|
|||||||||||||||||
|
|
|
|
|
|
|
2 cos |
|
|
|
2 |
|
|
6 |
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(мы |
воспользовались |
равенством |
|
|
|
|
|
|
4 64 = |
|
8 = 2 |
2 ). |
||||||||||||||||||||||||||||
Подставляя |
значения |
|
k = 0,1, 2,3 , |
|
найдем |
|
четыре |
|
различные |
|||||||||||||||||||||||||||||||
значения 4 |
z : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
= 2 |
2 |
|
cos |
π |
+i sin |
π |
= 2 |
2 |
|
|
|
|
3 |
|
+i |
1 |
|
= |
6 + |
|
2i; |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
0 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ω1 = 2 |
|
|
|
2π |
+i sin |
|
2π |
= |
|
|
|
|
|
|
− |
|
1 |
|
+i |
|
3 |
|
= − |
2 + |
6i; |
|||||||||||||||
2 |
cos |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
3 |
|
|
2 |
|
|
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ω2 |
= 2 |
2 |
|
|
7π |
+i sin |
|
7π |
= − |
|
6 − |
|
2i; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos |
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ω = 2 |
2 |
|
cos |
5π |
+i sin |
|
5π |
= |
2 |
2 |
|
1 |
|
−i |
|
3 |
= |
|
2 − 6i. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Остальные значения k новых точек уже не дадут. Заметим, что, извлекая корень 4-й степени из числа z = 32(−1+ 3i) , мы решали задачу, обратную той, которая разбиралась в примере 2.4, и корень ω3 = 2 − 6i оказался равным тому числу, которое возводилось в 4-ю степень. Но, кроме числа ω3 , будет
еще 3 различных значения |
4 z |
соответствующие точки |
|
ω0 , ω1, ω2 , ω3 |
расположены |
в |
вершинах правильного |
15

четырехугольника (т.е. квадрата) с центром в начале
координат и удалены от начала координат на расстояние 2 2 . Возможность извлекать корень из любого числа
позволяет решать квадратные уравнения az2 +bz +c = 0 с
произвольными (вообще говоря, комплексными) коэффициентами a,b, c . Корни уравнения находятся по
формуле
z |
= |
−b ± |
b2 −4ac |
, |
(2.13) |
|
|
||||
1,2 |
|
|
2a |
|
|
|
|
|
|
|
которая выводится так же, как и в случае действительных чисел a,b, c, z (путем выделения полного квадрата из
квадратного трехчлена az2 +bz +c ). В качестве b2 −4ac можно взять любое из двух значений корня; эти значения связаны равенством ω1 = −ω2 .
Пример 2.6. Решить уравнение z2 +2z +2 = 0 .
Решение. D = b2 −4ac = 4 −4 1 2 = 4 −8 = −4;
|
D = −4 = −1 4 = 2 −1 = ±2i . |
|||||
По формуле (2.13) |
|
|
|
|
|
|
z = −2 ±2i = −1±i; |
z = −1+i; |
z |
2 |
= −1−i. (Рис. 1.8) |
||
1,2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
В школьном курсе математики считается, что если |
||||||
дискриминант D < 0, то корней нет. Их и в самом деле нет, |
||||||
|
|
если искать только действительные |
||||
|
|
корни (т.е. точки, расположенные на |
||||
|
|
оси ОХ). Но среди более широкого |
||||
|
|
множества |
|
|
комплексных чисел |
|
|
|
корни |
|
|
уже |
найдутся; |
|
|
соответствующие |
точки |
|||
|
|
расположены |
вне |
действительной |
||
|
|
оси. |
|
|
|
|
|
Рис. 1.8 |
Таким образом, каждое квадратное |
||||
уравнение имеет ровно два корня (возможно, совпадающих).
16

6. В заключение введем еще одну форму записи комплексных чисел. Определим показательную функцию от
чисто мнимого аргумента iϕ следующим равенством: |
|
eiϕ = cosϕ +i sinϕ . |
(2.14) |
Поскольку число z можно записать в виде z = r(cosϕ +i sinϕ) , где r = z , то получаем более краткую, так называемую
показательную форму комплексного числа: z = reiϕ , r = z .
Пусть |
z |
= r eiϕ1 |
, |
z |
2 |
= r eiϕ2 . |
|
Учитывая формулы (2.5), |
(2.7) и |
|||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2.8), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r r eiϕ1 eiϕ2 |
= z z |
2 |
= r r ei(ϕ1 +ϕ2 ) , откуда eiϕ1 eiϕ2 = ei(ϕ1 +ϕ2 ) ; |
|||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
1 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
(reiϕ )n = zn = rneinϕ , откуда (eiϕ )n |
= einϕ ; |
|
|
|
|||||||||||||||||||
|
|
|
r e |
iϕ1 |
|
z |
|
|
|
r |
|
|
|
−ϕ2 ) |
|
e |
iϕ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
i(ϕ |
1 |
|
1 |
= e |
i(ϕ −ϕ |
) |
|
|
||||||||
|
|
|
1 |
|
|
= |
|
1 |
|
= |
|
1 |
e |
|
|
|
, откуда |
|
|
1 2 |
|
. |
(2.15) |
|||
|
|
r eiϕ2 |
z2 |
|
|
|
|
|
eiϕ2 |
|
||||||||||||||||
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, функция eiϕ , определенная равенством (2.14), обладает обычными свойствами показательной функции, что говорит о естественности такого определения. Формула (2.14)
называется формулой Эйлера.
17
2. ПОНЯТИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 2.1. Плоскость комплексного переменного
Если х и у являются переменными величинами (т.е. могут принимать различные значения), то z = x +iy называется
комплексным переменным. При изменении х и у
соответствующая |
|
точка |
z = x +iy |
пробегает |
|
|
|
|
некоторое |
|||||||||||||||||
множество точек комплексной плоскости |
|
. Вся комплексная |
||||||||||||||||||||||||
плоскость |
|
называется |
также плоскостью комплексного |
|||||||||||||||||||||||
переменного z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Расстояние ρ(z1, z2 ) между двумя точками |
z1 = x1 +iy1 |
и |
|||||||||||||||||||||||
z2 |
= x2 +iy2 находится по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
ρ(z z ) = (x − x )2 |
+( y − y |
2 |
)2 |
= |
|
|
z − z |
2 |
|
. |
|
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
1 |
1 |
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
Поэтому уравнение окружности радиуса R с центром в точке |
||||||||||||||||||||||||||
z0 |
имеет |
вид |
|
z − z0 |
|
= R , |
а множество точек |
z, |
|
лежащих |
||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
внутри круга радиуса R с |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
центром |
|
|
|
|
|
z0 , |
|
|
|
|
|
задается |
||||
|
|
|
|
|
|
|
|
|
|
неравенством |
|
|
|
|
|
z − z0 |
|
< R |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
(рис.2.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
||
|
|
|
|
|
|
|
|
|
|
Для фиксированной точки |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
плоскости |
|
|
|
комплексного |
||||||||||||
|
|
|
|
|
|
|
|
|
|
переменного |
|
|
|
|
|
|
|
|
и |
|||||||
|
|
|
|
|
|
|
|
|
|
положительного |
|
|
числа |
δ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
множество всех точек z, |
||||||||||||||||
|
|
Рис. 2.1 |
|
|
|
|
|
удовлетворяющих |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
неравенству |
|
|
|
z − z0 |
|
|
<δ , |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
является внутренностью круга |
|||||||||||||||||
радиуса |
S с |
|
центром |
z0 . |
Это |
множество |
|
называется |
||||||||||||||||||
δ -окрестностью точки z0 .
Множество D точек называется открытым, если всякая его точка имеет окрестность, принадлежащую D (т.е. целиком
18

состоящую из точек данного множества D). Например,
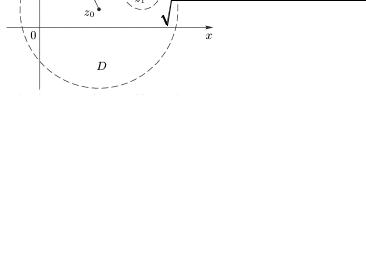
множество |
|
|
D ={z : |
|
z − z0 |
|
< R} |
|
|
(см. |
рис. |
2.1) |
является |
|||||||||||
|
|
|||||||||||||||||||||||
открытым. |
Действительно, |
возьмем любую |
точку |
z1 D . |
||||||||||||||||||||
Тогда |
|
z − z0 |
|
|
< R , |
и d = R − |
|
z1 − z0 |
|
> 0 будет расстоянием от z1 |
||||||||||||||
|
|
|
|
|||||||||||||||||||||
до окружности |
|
|
z − z0 |
|
= R . |
Поэтому |
если |
0 <δ < d , |
то |
|||||||||||||||
|
|
|
||||||||||||||||||||||
множество |
|
|
z − z0 |
|
<δ лежит в |
D; это и доказывает, что |
D |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
открыто.
Множество D называется связным, если любые две точки из D можно соединить непрерывной кривой, целиком лежащей в D. Открытое связное множество называется областью.
Приведем |
примеры областей: круг |
|
z − z0 |
|
|
< R ; кольцо |
||||
|
|
|||||||||
r < |
|
z − z0 |
|
|
< R , 0 ≤ r < R ; вся плоскость |
; |
полуплоскость |
|||
|
|
|||||||||
Re z > a , где a — действительное число. В то же время круг
|
z − z0 |
|
≤ R не является областью, так как это |
множество не |
||||
|
|
|||||||
является открытым: для точек z, для которых |
|
|
z − z0 |
|
= R , не |
|||
|
|
|||||||
существует окрестности, целиком лежащей в этом круге.
Точка z1 называется граничной точкой множества D,
если в любой окрестности точки z1 найдутся как точки,
принадлежащие множеству D, так и точки, ему не принадлежащие. Множество граничных точек называется границей множества D. Множество, состоящее из области D и всех граничных точек области D, называется замкнутой
областью и обозначается |
D |
. Например, круг |
|
|
|
z − z0 |
|
≤ R |
и |
||||||||||
|
|
||||||||||||||||||
кольцо r ≤ |
|
z − z0 |
|
≤ R являются замкнутыми областями; |
но |
||||||||||||||
|
|
||||||||||||||||||
кольцо r < |
|
z − z0 |
|
|
≤ R не является замкнутой областью (так как |
||||||||||||||
|
|
||||||||||||||||||
граничные точки, лежащие на окружности |
|
z − z0 |
|
= r , |
не |
||||||||||||||
|
|
||||||||||||||||||
принадлежат этому множеству), и не является областью (данное множество содержит граничные точки на окружности
z − z0 = R и, следовательно, не будет открытым).
19
Области на плоскости делятся на односвязные и многосвязные. Область называется односвязной, если ее
граница состоит из одной непрерывной кривой без
самопересечений |
|
||||||
(возможно, замкнутой). |
|
||||||
Например, |
|
круг |
Рис. 10 |
||||
|
z − z0 |
|
< R |
|
и |
||
|
|
|
|||||
|
|
|
|
||||
полуплоскость |
являются |
|
|||||
односвязными областями. |
|
||||||
Область, не |
являющаяся |
|
|||||
односвязной, |
называется |
|
|||||
многосвязной. |
В |
|
|||||
частности, |
многосвязная |
Рис. 2.2 |
|||||
область называется n-связной, |
|||||||
|
|||||||
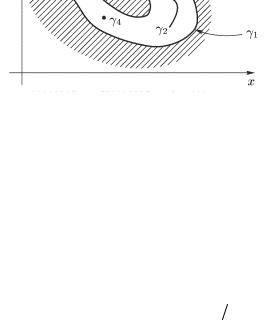
если ее граница состоит из n (n > 1) непересекающихся непрерывных кривых; некоторые из них могут вырождаться в точку. Например, на рис. 2.2 изображена 4-х связная область D; ее граница состоит из четырех кривых γ1,γ2 ,γ3 ,γ4.
Рассмотрим еще одну геометрическую интерпретацию
комплексного числа. Пусть S — |
сфера радиуса 1 2 , |
касающаяся комплексной плоскости |
в точке z = 0 (рис. 2.3), |
и Р — точка сферы, диаметрально противоположная точке 0. Возьмем произвольную точку z и проведем луч Pz . Этот
луч имеет единственную точку пересечения Z со сферой S;
очевидно, что Z ≠ P . |
Тем |
самым |
каждой |
точке z |
поставлена в соответствие точка Z S , Z ≠ P . Наоборот, если |
||||
задана точка Z S , Z ≠ P , то аналогичное построение дает |
||||
соответствующую точку |
z |
. Тем |
самым |
мы построили |
взаимно однозначное соответствие между точками комплексной плоскости и точками сферы S, отличными от
Р. Это соответствие называется стереографической проекцией.
20
