Учебное пособие 1865

ϕ(z) не имеет нулей и в некоторой окрестности этой точки. Поэтому функция 1ϕ(z) будет также аналитической в этой окрестности и, следовательно, разлагается в ней в ряд Тейлора:

Раскрывая скобки и меняя обозначения коэффициентов, запишем последнее разложение в виде

где c−N = b0 ≠ 0 . Таким образом, главная часть лорановского

разложения функции f(z) содержит лишь конечное число членов; мы пришли к искомому равенству (7.2).

2. Пусть в проколотой окрестности точки z0 функция f(z) представляется лорановским разложением (7.2) (в более развернутом виде см. (7.3)), главная часть которого содержит лишь конечное число членов, причем c−N ≠ 0 . Надо доказать,

что z0 — полюс функции f(z). Умножая равенство (7.3) на (z — z0)N, получим функцию

h(z) = f (z)(z − z0 )N = c−n+1 (z − z0 ) +c−N +2 (z − z0 )2 +... (7.4)

Ряд в (7.4) является степенным рядом, сходящимся к аналитической функции не только в проколотой, но и во всей окрестности точки z0. Поэтому функция h(z) станет

151

аналитической в этой окрестности, если доопределить ее в z0, положив h(z0) = c−N ≠ 0 . Тогда

Таким образом, точка z0 является полюсом, и теорема 7.3 доказана.

Кратность (порядок) нуля z0 функции g(z) = 1/f(z)

называется порядком полюса z0 функции f(z). Если N — порядок полюса z0, то g(z) = (z — z0)Nϕ(z) , причем ϕ(z) ≠ 0 , и,

как показано в первой части доказательства теоремы 26.3, разложение функции f(z) имеет вид (7.3), где c−N ≠ 0 . Обратно,

если f(z) раскладывается в ряд (7.3) и c−N ≠ 0 , то

т.е. N — порядок полюса функции f(z). Таким образом, порядок полюса z0 функции f(z) равен номеру старшего ненулевого коэффициента главной части лорановского разложения в проколотой окрестности точки z0 (т.е. равен такому числу N,

что c−N ≠ 0 и сп = 0 при п > N).

Докажем следующее утверждение, удобное для применений.

Следствие 7.4. Точка z0 является полюсом порядка N функции f(z) тогда и только тогда, когда f(z) представима в

где h(z) — аналитическая функция в окрестности точки z0 и h(z0 ) ≠ 0 .

Доказательство. Функция ϕ(z) =1h(z) аналитична в

некоторой окрестности точки z0. Условие следствия 7.4 равносильно следующему:

152

Поэтому z0 — нуль кратности N функции g(z), а значит, и полюс кратности N функции f(z).

Пример 7.5. Найти изолированные особые точки

то z = -3. Поэтому функция имеет три особые точки z1=i, z2=-i, z3= -3. Рассмотрим z1:

полюс первого порядка (мы воспользовались следствием 7.4). Аналогично доказывается, что z2 = -i тоже полюс первого порядка. Для z3 имеем

рядка.

Перейдем к рассмотрению существенно особых точек.

Теорема 7.6. Изолированная особая точка z0 функции f(z) является существенно особой тогда и только тогда, когда главная часть разложения Лорана с центром z0 имеет бесконечно много отличных от нуля коэффициентов сп.

Доказательство. Теорема 7.6 непосредственно вытекает из теорем 7.2 и 7.3. Действительно, если точка z0 — существенно особая, то главная часть лорановского

153

разложения не может отсутствовать либо содержать конечное число членов (в противном случае точка z0 будет либо устранимой, либо полюсом). Поэтому число членов в главной части должно быть бесконечным.

Обратно, если главная часть содержит бесконечно много членов, то z0 не может быть ни устранимой точкой, ни полюсом. Следовательно, эта точка — существенно особая.

Согласно определению, существенно особая точка характеризуется тем, что функция f(z) не имеет ни конечного, ни бесконечного предела при z → z0 . Полное представление о

том, насколько нерегулярным является поведение функции в окрестности существенно особой точки, дает следующая теорема.

lim f (zn ) = A .

n→∞

Доказательство. Рассмотрим вначале случай A = ∞. В первой части доказательства теоремы 7.2 мы установили, что если f(z) ограничена в некоторой проколотой окрестности точки z0, то все коэффициенты сn, п = - 1, - 2,... главной части равны нулю (и, следовательно, особенность в z0 устранимая). Так как по условию z0 существенно особая точка, то в любой проколотой окрестности точки z0 функция f(z) является неограниченной. Возьмем некоторую проколотую окрестность

0 < z − z0 < R , в которой f(z) является аналитической. В этой окрестности найдется точка z1, такая что f (z1 ) >1 (если бы f (z1 ) <1 во всех точках, то f(z) была бы ограниченной). Точно

154

образом, в случае A = ∞ теорема 26.7 доказана.

Пусть теперь A ≠ ∞ . Предположим вначале, что найдется проколотая окрестность 0 < z − z0 < R1 , в которой f (z) ≠ A .

проколотой окрестности и, следовательно, z0 является изолированной особой точкой функции ψ(z) . Покажем, что z0

— существенно особая точка ψ(z) . Пусть это неверно. Тогда

что противоречит условию теоремы. Таким образом, z0 — существенно особая точка функции ψ(z) . Согласно

доказанному выше, найдется последовательность точек zn,

Предположим теперь, что это неверно, т.е. в любой сколь угодно малой проколотой окрестности точки z0 найдется такая точка z', что f(z') = А. Тогда для любого п в проколотой

окрестности 0 < z − z0 < R n можно выбрать такую точку zn.

Мы получим последовательность точек, для которых f(zn) = А и

zn → z0 . Поэтому и lim f (zn ) = A . Таким образом, нужное

n→∞

утверждение справедливо во всех случаях, и теорема 7.7 доказана.

Согласно теореме 7.7 (Сохоцкого), в любой (сколь угодно малой) проколотой окрестности существенно особой точки

155

функция f(z) принимает значения, сколь угодно близкие к

любому числу из расширенной комплексной плоскости . Для исследования изолированных особых точек часто

бывают полезными уже известные тейлоровские разложения основных элементарных функций.

Пример 7.8. Определить тип особой точки z0 = 0 для функции

f (z) = e3z −1 .

(sin z) − z + z3 6

Решение. Разложим числитель и знаменатель в ряд Тейлора по степеням z. Подставляя в (2.11) 3z вместо z и вычитая 1, получим

Используя (2.12), получим разложение знаменателя:

Ряды в этих разложениях сходятся во всей комплексной плоскости . Имеем

и f2(z) аналитичны в окрестности точки z0 = 0 (и даже во всей плоскости) и f2 (z0 ) ≠ 0 , то h(z) также аналитична в некоторой

окрестности точки z0 = 0; при этом h(0) = 3 5! ≠ 0 . Согласно следствию 26.4, точка z0 = 0 является полюсом порядка N = 4.

156

проколотой окрестности точки z0 = 1. Поскольку полученное разложение содержит бесконечно много членов с отрицательными степенями (z — 1), то z0 = 1 — существенно особая точка (в данном случае лорановское разложение состоит только из главной части, а правильная часть отсутствует).

Заметим, что установить характер особенности в данном случае можно было и непосредственно из определения, не прибегая к разложению в ряд. Действительно, существуют последовательности {z'n} и {z''n}, сходящиеся к z0 = 1, и такие, что f(z'n) = 1, f(z''n) = 0 (укажите такие последовательности самостоятельно). Значит, f(z) не имеет предела при z →1 и, следовательно, точка z0 = 1 является существенно особой.

Введем понятие лорановского разложения функции в окрестности точки z0 = ∞ и рассмотрим связь разложения с

характером особенности в этой точке. Отметим, что определения изолированной особой точки и ее типа

157

(устранимая, полюс либо существенно особая) переносятся на случай z0 = ∞ без изменений. Но теоремы 7.2, 7.3 и 7.6,

связанные с характером лорановских разложений, нуждаются в изменении. Дело в том, что члены cn(z — z0)n, п = -1,-2,..., главной части, определяющие "нерегулярность" функции вблизи конечной точки z0, при стремлении z к ∞ будут вести себя "правильно" (стремиться к 0). Напротив, члены правильной части с n = 1,2,... будут стремиться к ∞; они и определяют характер особенности в z0 =∞ . Поэтому главную

часть разложения в окрестности ∞ будут составлять члены с положительными степенями n, а правильную — с отрицательными.

Введем новое переменное w = 1/z. Функция w = 1/z, доопределенная так, что w(∞) = 0 , взаимно однозначно и

проколотой окрестности 0 < w <1 R точки w0 = 0. Так как при

z → ∞ будет w → 0 , то

lim f (z) = lim G(w) .

z→∞ w→0

Поэтому G(w) имеет в точке w0 = 0 особенность того же типа, что f(z) в точке z0 = ∞ . Разложим функцию G(w) в ряд Лорана

в проколотой окрестности точки w0 = 0:

Суммы в правой части (7.5) представляют правильную и главную части разложения соответственно. Перейдем к переменному z, подставив w = 1/z:

158

Разложение (7.6) называется разложением Лорана функции f(z) в проколотой окрестности точки z0 = ∞ . Первая сумма в

(7.6) называется правильной частью, а вторая сумма — главной частью этого разложения. Поскольку эти суммы соответствуют правильной и главной частям разложения (7.5), то для разложения (7.6) справедливы аналоги теорем 7.2, 7.3 и 7.6. Так, аналогом теоремы 7.2 будет следующая теорема.

Теорема 7.10. Изолированная особая точка z0 = ∞

функции f(z) является устранимой тогда и только тогда, когда лорановское разложение в проколотой окрестности этой точки имеет вид

называется аналитической в точке z0 = ∞ . (Заметим, что это

определение равносильно аналитичности функции G(w) в точке w0 = 0.)

159

соответствующее разложение (7.7). Перейдем к переменному w = 1/z. Подставляя z = 1/w, получим

(последнее равенство справедливо в проколотой окрестности точки w0 = 0, но мы доопределим G(0) = 0). Полученная функция имеет особые точки w = ±i , w = −1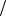3 , а в точке w0 = 0 является аналитической. Раскладывая функцию G(w) по степеням w (как это делалось в примере 6.7) и подставляя в полученный степенной ряд w = 1/z, можно получить разложение (7.7) функции f(z).

Теорема 7.3 для случая z0 = ∞ перепишется в следующем

виде.

Теорема 7.12. Изолированная особая точка z0 = ∞

функции f(z) является полюсом тогда и только тогда, когда главная часть разложения Лорана (7.6) имеет лишь конечное число отличных от нуля коэффициентов сп:

n=0

Здесь ряд является правильной частью, а многочлен в скобках — главной частью разложения. Кратность полюса в ∞ определяется как кратность полюса w0 = 0 функции G(z). Легко видеть, что кратность полюса совпадает с числом N в (7.8).

имеет в точке z0 = ∞ полюс порядка 3.

160