Учебное пособие 1865

Решение. Из условий Коши-Римана (1.4) находим

этом постоянная C = C( y) не должна зависеть от x, но может зависеть от у:

u = ∫(4x +1)dx = 2x2 + x +C( y).

Для нахождения функции C( y) подставим u в уравнение

(2.4):

∂∂uy = C′( y) = −4 y .

Отсюда C( y) = ∫(−4y)dy = −2y2 +C1 , где C1 — произвольная

постоянная. Итак,

u = 2x2 + x −2y2 +C1,

f (z) = u +iv = (2x2 + x −2 y2 ) +i(4xy + y) +C1.

Можно записать f (z) и в другой форме:

f(z) = 2(x2 +2ixy − y2 ) + x +iy +C1 =

=2(x +iy)2 +(x +iy) +C1 = 2z2 + z +C1.

41

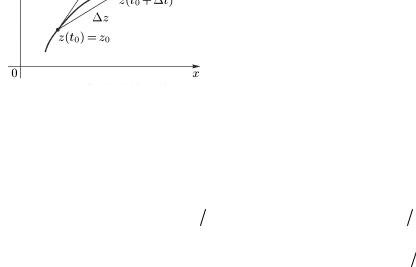
3.3. Геометрический смысл производной функции комплексного переменного. Понятие конформного отображения

1. Геометрический смысл аргумента производной.

Напомним вначале некоторые сведения о кривых. Каждая кривая на плоскости может быть задана параметрическими уравнениями

где x(t), y(t) — действительные функции действительного переменного t. В дальнейшем предполагается, что эти функции имеют непрерывные производные на интервале (α, β) , причем

будет поворачиваться, приближаясь к вектору

42

z(t0 ) , называется касательной к кривой в этой точке. Таким

(рис. 3.3, a), a ω′(t0 ) — вектор, касательный к кривой Г в точке

43

Возьмем какие-либо две кривые γ и γ1 проходящие через точку z0 , и проведем касательные к этим кривым (рис. 3.3, а). При отображении ω = f (z) кривые γ и γ1 перейдут в

Рис. 3.3

кривые Г и Г1 , а каждая из касательных к γ и γ1 повернется на один и тот же угол. Поэтому угол θ между касательными к γ и γ1 будет равен (как по величине, так и по направлению отсчета) углу между касательными к Г и Г1 . Напомним, что углом между кривыми в точке z0 называется угол между касательными к этим кривым в точке z0 . Таким образом, если f ′(z0 ) ≠ 0 , то отображение ω = f (z) сохраняет углы между кривыми.

2.Геометрический смысл модуля производной.

44

то модуль f ′(z0 ) равен коэффициенту растяжения в точке z0 при отображении ω = f (z) . Если f ′(z0 ) >1, то в достаточно малой окрестности точки z0 расстояния между точками при отображении увеличиваются и происходит

Рис. 3.4

растяжение; если f ′(z0 ) <1, то отображение приводит к

сжатию (хотя соответствующий коэффициент все равно называют коэффициентом растяжения).

Так как производная f ′(z0 ) не зависит от того, по какому пути точка z0 + z приближается к z0 , то коэффициент

растяжения одинаков во всех направлениях. Это свойство можно проиллюстрировать следующим образом. Возьмем

45

точке z0 . При этом Arg f ′(z0 ) означает угол поворота, a

отображении.

Пример конформного отображения второго рода дает

функция (не аналитическая!) ω = z , которая каждую область D отображает на область Е, симметричную D относительно оси

ОХ.

Если f ′(z0 ) = 0 , то отображение, вообще говоря, уже не будет конформным в точке z0 . Так, отображение ω = z2 увеличивает вдвое углы между лучами в начале координат.

47

4. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ

Функция ω = f (z) называется однолистной в области D,

если в разных точках области D эта функция принимает разные значения: если z1 ≠ z2 , то f (z1 ) ≠ f (z2 ) .

Пусть функция f (z) отображает область D на область Е.

Однолистность означает, что каждая точка ω E имеет только один прообраз в D. Поэтому отображение области D на

в полуплоскости D ={z : Re z > 0} .

Отображение области D на область Е называется конформным, если оно непрерывно и конформно в каждой точке области D.

Из теоремы 3.1 следует, что если функция f (z) аналитична в области D и f ′(z) не обращается в нуль ни в

одной точке из D, то эта функция осуществляет конформное отображение области D.

Перейдем к изучению основных элементарных функций и свойств соответствующих отображений.

где a и b — заданные комплексные числа a ≠ 0 , называется

также однолистно в . Если ω1 = az1 +b , ω2 = az2 +b , то

48

ω1 −ω2 = a(z1 − z2 ) . Поэтому при z1 ≠ z2 получаем, что ω1 ≠ω2

иоднолистность установлена. Положив по определению

ω(∞) = ∞ , получим однолистное отображение всей

z = z eiϕ . Тогда

ω = a z ei(α+ϕ) .

Поэтому для получения вектора ω = az нужно выполнить следующие два действия:

1) умножить заданный вектор z на a . При этом

преобразование подобия (гомотетия) с центром в начале координат и коэффициентом подобия a ;

2) повернуть полученный вектор a z на угол α .

Для рассмотрения общего случая (1.1) заметим, что при сложении вектора az с вектором b происходит параллельный перенос концевой точки вектора az на вектор b .

Итак, отображение (1.1) получается путем композиции (т.е. последовательного выполнения) следующих трех операций: 1) преобразования подобия с центром в начале

координат и коэффициентом подобия a ; 2) поворота вокруг

начала координат на угол α ; 3) параллельного переноса на вектор b .

Пример 4.1. Найти линейную функцию, отображающую квадрат D со стороной 2 на квадрат Е со стороной 4 (рис. 4.1) и точку А в точку В.

49

коэффициент подобия равен 2, то нужное преобразование есть

Очевидно, что нужный поворот будет на угол 45° против

3. Осталось сделать параллельный перенос квадрата D2 на вектор A2 B . Учитывая, что B = 6 +2i , имеем A2 B = 4 −4i и

ω=ω2 +4 −4i . Итак,

ω=ω2 +4 −4i =ω1eiπ 4 +4 −4i = 2zeiπ 4 +4 −4i ,

иискомое линейное отображение ω = az +b получено:

a = 2eiπ4 = 2 +i 2; b = 4 −4i .

50