
Механика (кинематика). Учебное пособие. Рябцев В.А
.pdfВ. А. Рябцев
МЕХАНИКА
(КИНЕМАТИКА)
Учебное пособие
Воронеж 2004
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
В. А. Рябцев
МЕХАНИКА
(КИНЕМАТИКА)
Утверждено Редакционно–издательским советом университета в качестве учебного пособия
ВОРОНЕЖ 2004

УДК 531.1/2
Рябцев В.А. Механика (кинематика): Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2004. 125 с.
В учебном пособии рассмотрены основные сведения по разделу кинематика точки и твердого тела дисциплины «Механика». Изложение теории сопровождается примерами решения типовых задач. К каждой главе приведена подборка задач для самостоятельного решения. Учебное пособие может быть рекомендовано для самостоятельного изучения соответствующих разделов и тем курса механики.
Издание соответствует рабочим программам курсов «Прикладная механика» и «Механика». Учебное пособие предназначено для студентов специальностей 140601, 140604, 280103, 110302 всех форм обучения.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97 и содержится в каталоге
«PosMehanKin».
Ил. 109. Библиогр.: 5 назв.
Научный редактор канд. техн. наук, доц. А.А. Воропаев
Рецензенты: кафедра естественно – научных дисциплин Международного института компьютерных технологий; канд. физ.- мат. наук, доц. В.Н. Потапов
Рябцев В. А. 2004
Оформление. Воронежский государственный технический университет, 2004
ВВЕДЕНИЕ
Вучебном пособии рассмотрены основные сведения по разделам кинематика точки и твердого тела дисциплины «Механика». Учебное пособие написано в соответствии с программой курса «Механика», утвержденной Министерством образования РФ и требованиями ГОС специальностей «Системы автоматизированного проектирования», «Защита в чрезвычайных ситуациях» и др.
Вотличие от традиционного за основу построения посо-
бия принят дедуктивный метод изложения. Это позволило при изложении некоторых тем существенно уменьшить объем материала и сократить время, необходимое для изучения теории. Тем самым удалось дать сразу общие методы решения различных типовых задач, с которыми будущий инженер вероятнее всего встретится в своей практической деятельности после окончания учебного заведения.
Для лучшего усвоения теоретических положений изложение каждого раздела теории сопровождается примерами решения типовых задач, выполненными сначала в векторном виде, затем в алгебраическом виде, а затем в числовом. В конце каждой главы приведена подборка задач для самостоятельного решения. Учебное пособие может быть рекомендовано для самостоятельного изучения соответствующих разделов и тем курса механики.
Единицы измерения приняты в соответствии с Международной системой единиц измерения (СИ).
Для дальнейшего изучения излагаемого материала в учебном пособии приведен список дополнительной литературы.
Автор будет благодарен читателям, которые сообщат на кафедру прикладной механики свои пожелания и критические замечания, для учета их в дальнейшей работе по совершенствованию данного учебного пособия.
3
Глава 1. КИНЕМАТИКА ТОЧКИ
§ 1.1. Основные понятия
Раздел «Теоретическая механика» дисциплины «Механика» состоит из трех частей: кинематики, статики и динамики. Теоретическая механика наука физико-математическая. С одной стороны в ней используются аксиомы, из которых логически получаются все нужные теоремы. С другой стороны, предметом изучения теоретической механики являются физические процессы и, следовательно, для применения к ним теории нужно создавать схемы реальных явлений.
Теоретическая механика является теоретической базой многих технических дисциплин, например сопротивления материалов, теории механизмов и машин, деталей машин и других, без знания которых немыслимо стать современным специалистом.
Ни одна наука не обходится без абстракций, идеализированных схем реальных явлений. Расчетной схемой является абстракция реального явления. Она получается при введении некоторых упрощающих предположений, не учитывающих некоторые несущественные факторы. Важнейшими для всей теоретической механики являются две абстракции: материальная точка и абсолютно твердое тело.
Материальной точкой называют тело, обладающее бесконечно малой или конечной массой, размеры которого в рассматриваемом явлении несущественны.
Жесткой системой материальных точек, называют такую систему (совокупность) материальных точек, у которой расстояния между любыми двумя точками постоянны. Частным случаем такой системы является абсолютно твердое (жесткое) тело, точки которого полностью или частично заполняют некоторую область пространства.
92
Если несколько твердых тел образуют между собой подвижные соединения, то эти тела в технике называю звеньями.
Если при заданных движениях одного или нескольких звеньев другие звенья совершают закономерные движения, то такое соединение звеньев называется механизмом.
В природе и технике не существуют ни материальные точки, ни абсолютно твердые тела. Абстракцией «материальная точка» можно пользоваться при описании явлений, в которых формы и размеры тела несущественны, но необходимо учесть массу тела, например, при изучении падения тел в вакууме, при вычислении кинетической энергии тела в поступательном движении и т.д. Во всех подобных случаях тело заменяется одной из точек этого тела. Обычно за эту точку принимают центр масс тела, считая, что в ней сосредоточена масса всего тела.
Абстракция «абсолютно твердое тело» используется в тех явлениях, для которых масса, форма и размеры тела существенны, но изменения формы - деформации настолько малы, что ими можно пренебречь. На такой абстракции основана, например, вся аэрогидромеханика, так как аэро- и гидродинамические силы весьма чувствительны к размерам и форме движущихся телсамолетов, кораблей и подводных лодок. Следовательно, самолеты и корабли должны быть настолько жесткими, чтобы неизбежно возникающие при их движении деформации были малыми и не влияли существенно на аэродинамические силы, например на лобовое сопротивление или подъемную силу самолета. Таким же образом при определении реакций опор на жесткие тела в технике можно пренебрегать малыми деформациями этих тел. Однако, всякая абстракция по самой своей сути конкретна, так как она относится к определенному кругу явлений и не может автоматически переноситься на другие явления. Например, при изучении внутренних сил в телах и изучении их прочности нужно учитывать те малые деформации, которыми можно пренебрегать при определении реакций опор.
93

§ 1.2. Основы векторной алгебры
Вектором в математике называется отрезок, имеющий определенную длину и направление.
Вектор, который можно переносить параллельно самому себе в произвольную точку пространства называется свободным вектором. Если вектор можно переносить только вдоль
прямой, на которой находится вектор, то такой вектор называется скользящим. Вектор, для определения которого важны координаты его начала называется связанным. Векторы изображаются на чертежах в масштабе. Вектор может быть определен своими проекциями на оси некоторой системы координат.
Векторы суммируются по правилам параллелограмма (рис.1.1). Сумма двух векторов, равна по величине и направлению диагонали параллелограмма, построенного на этих векторах, как на сторонах (рис. 1.1).
Параллелограмм на рис. 1.1 построен в определенном масштабе, т. е. выбранная единица длины соответствует единице длины вектора. Поэтому, например, запись AB = P2 означает, что число единиц длины в отрезке AB равно числу единиц
|
|
|
|
|
|
силы P2. Сумма R |
двух векторов P1 и P2 |
записывается в виде |
|||
|
|
|
|
|
|
|
R |
P1 |
P2 . |
|
(1.1) |
Суммирование по правилу параллелограмма называют |
|||||
векторным суммированием. |
|
|
|
||
Отрезок AB равен и параллелен отрезку ОС. Поэтому, если |
|||||
|
|
|
|
|
|
мысленно (на самом деле вектор P |
приложен в точке О) от- |
||||
|
|
|
2 |
|
|
ложить вектор P2 |
от конца А вектора P1 |
, то сумма векторов R |
|||
имеет начало в начале первого вектора и конец - в конце второ-
94
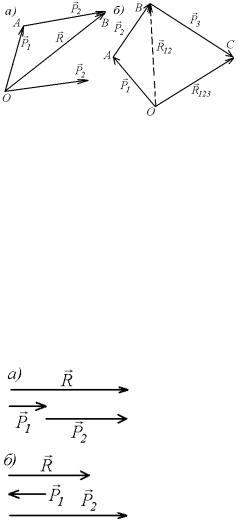
го вектора. Такое правило сложения векторов называется правилом векторного треугольника (рис. 1.2, а).
|
|
|
|
|
Рассмотрим |
пучок |
|
|
|
|
|
векторов, т. е. систему |
|||
|
|
|
|
векторов, приложенных в |
|||
|
|
|
|
одной точке (рис. 1.2, |
б). |
||
|
|
|
|
|
|
|
|
|
|
|
|
Складывая векторы P1 |
и |
||
|
|
|
|
|
|
|
|
|
|
|
|
P2 |
по правилу треуголь- |
||
Рис. 1.2. |
|
|
ника, получаем их сумму |
||||
|
|
|
. Затем по |
тому |
же |
||
|
|
|
|
R12 |
|||
|
|
|
|
|
|
||
правилу складывая |
R12 |
и |
P3 |
, получаем сумму R123 трех векто- |
|||
ров. Процесс сложения продолжается до тех пор, пока не будут
просуммированы все векторы и получена сумма R . Ломаную линию OABC, отрезки которой равны и параллельны данным векторам, называют векторным многоугольником. Отсюда следует правило векторного многоугольника: чтобы сложить систему векторов надо от конца первого вектора отложить второй
вектор, от конца второго вектора отложить третий вектор и т. д.
Суммарный вектор R имеет начало в начале первого вектора и конец — в конце последнего вектора.
Рис. 1.3.
наглядности векторы
Сложение векторов по правилу параллелограмма называют векторным суммированием, а так как правило, векторного многоугольника получено как
следствие правила параллелограмма, то
вектор R , замыкающий векторный многоугольник, называют векторной суммой.
Рассмотрим частный случай векторного многоугольника, при расположении векторов на одной прямой (рис. 1.3). Для
|
|
|
|
|
|
P1 |
, |
P2 |
и их векторная сумма |
R |
распо- |
ложены не по одной прямой, а рядом. Формула (1.1), также применима и в этом случае, но удобнее использовать простые
95
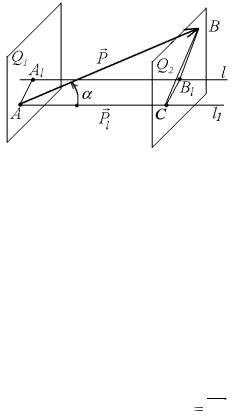
соотношения и между величинами (модулями) векторов. В случае, изображенном на рис. 1.3, а
R= P1 +P2 |
(1.2) |
Для случая, изображенного на рис. 1.3, б |
|
R = |P2 -P1)| |
(1.3) |
Следовательно, сумма векторов, направленных в одну сторону по одной прямой, направлена в ту же сторону. Ее модуль равен сумме модулей составляющих векторов. Если векторы направлены по одной прямой в противоположные стороны, то модуль их суммы равен модулю разности
модулей составляющих векторов, а суммарный вектор направлен в сторону вектора с большим модулем. Очевидно, что это заключение верно для суммы произвольного числа параллельных векторов.
Осью называют прямую, для которой одно из двух направлений вдоль этой прямой считается положительным.
Проекцией точки А на ось l (рис. 1.4) называют точку A1 пересечения плоскости, проходящей через точку А, перпендикулярно оси l .
Проекцией вектора P AB на ось l (рис. 1.4) называют скалярную величину, равную взятой с соответствующим знаком длине отрезка A1B1 оси l, заключенного между двумя плос-
костями, перпендикулярными оси l и проходящими через край-
ние точки вектора P .
Если движение от точки A1 к точке B1 происходит в положительном направлении оси, то проекция считается положи-
96

тельной. В противном случае проекция отрицательна. Так как плоскости Q1 и Q2 перпендикулярны оси l, то и прямые AA1 и
BB1 перпендикулярны этой же оси. Поэтому модуль Pl проек-
ции Pl = A1B1 вектора P AB можно получить, опустив пер-
пендикуляры из начала и конца вектора P на ось l.
Проведем другую ось l1 параллельно оси l. Ось l1 пересечется с плоскостью Q2 в точке С. Так как отрезки параллельных прямых между параллельными плоскостями равны, то AC = A1B1 = Pl . Следовательно, при определении проекции век-
тора на ось можно вектор или ось переносить параллельно самим себе так, чтобы получились пересекающиеся прямые, и вектор считать приложенным в какойлибо точке оси.
|
|
|
|
|
|
Углом |
между вектором |
P и по- |
|
|
ложительным направлением |
оси l1 |
||
|
(или l) называют угол, образованный |
|||
|
вращением |
против часовой |
стрелки |
|
|
оси l вокруг точки А до совпадения с |
|||
|
вектором. |
Этот угол обозначается |
||
Рис. 1.5. |
|
|
|
|
символом |
( P , l ) . Такое определе- |
|||
|
||||
ние угла позволяет дать единую формулу для нахождения величины проекции вектора на ось при всех возможном его расположении относительно оси (рис. 1.5)
|
Pl= Pcos , |
(1.4) |
|
|
|
где |
( P , l ) . |
|
|
|
|
|
Для положений, при которых вектор |
P расположен так, |
что, |
= 0° или = 180°, cos 0° = 1, cos 180°= -1. Поэтому для |
|
таких положений вектора Pl = ±Р. |
|
|
Итак, если вектор параллелен оси, то его проекция на эту ось равна модулю вектора, взятому со знаком плюс или минус
97
