
Учебное пособие 1828
.pdf
|
|
|
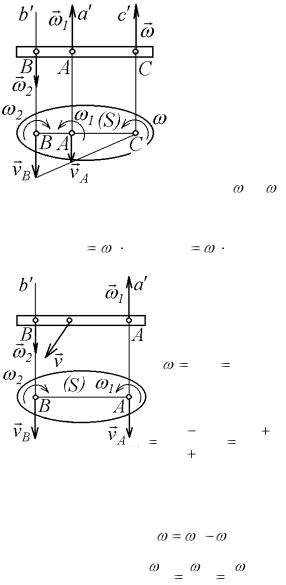
vB 1 AB . При этом векторы vA |
и vB |
будут |
параллельны друг другу (оба перпендикулярны АВ) и направлены в противоположные стороны. Тогда точка С (см. § 3.2) будет мгновенным
центром скоростей ( vC = 0), а следовательно,
ось Cc , параллельная осям aa
, параллельная осям aa и bb
и bb , будет мгновенной осью вращения тела.
, будет мгновенной осью вращения тела.
Для определения угловой скорости абсолютного вращения тела вокруг оси Cc и положения этой оси, т. е. точки С, используем равенство (3.5)
и положения этой оси, т. е. точки С, используем равенство (3.5)
|
|
|
|
|
|
|
vB |
|
vA |
. |
|
|
|||||
|
|
|
|
|
|
|
BC |
AC |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
Используя свойство пропорции, получаем |
||||||||||||||||
|
|
|
|
vA |
|
vB |
|
vA |
|
vB |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AC |
|
BC |
|
|
AB |
|||||||||
|
Подставляя в это и предыдущее равенства |
||||||||||||||||
vA |
2 AB , vB 1 AB , получим |
|
|
||||||||||||||
|
1 |
2 , |
|
|
|
|
(6.1) |
||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
. |
(6.2) |
||||
|
|
BC |
AC |
|
AB |
||||||||||||
Итак, если тело участвует одновременно в двух направленных в одну сторону вращательных движениях вокруг параллельных осей, то его результирующее движение будет мгновенным вращением с абсолютной угловой скоростью 1
1  2 вокруг мгновенной оси, параллельной
2 вокруг мгновенной оси, параллельной
данным осям, а положение этой оси определяется пропорцией (6.2).
188
С течением времени мгновенная ось вращения Cc будет менять свое положение, описывая цилиндрическую поверхность.
будет менять свое положение, описывая цилиндрическую поверхность.
6.2.2. Вращения направлены в разные стороны
Пусть для определенности, 1  2 . Тогда, рассу-
2 . Тогда, рассу-
ждая, как в предыдущем случае, получим, что модули линейных скоростей точек А и В будут
равны: vA |
|
2 AB , vB |
1 |
AB . Векторы скоро- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
стей v |
и |
v |
будут параллельны друг другу и |
|||||||||||||||
|
|
|
|
|
|
сторону. Тогда мгновенная |
||||||||||||
|
|
|
|
ходит через точку С (рис. |
||||||||||||||
|
|
|
|
|
|
|
|
vB |
|
|
|
vA |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
BC |
|
|
AC |
|
|
|||||
|
|
|
свойства пропорции, получаем |
|||||||||||||||
|
|
|
|
|
vB |
|
vA |
|
|
|
vB |
vA |
. |
|||||
|
|
|
|
|
BC |
|
AC |
|
|
|
|
AB |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставляя в эти равенства величины vA и |
||||||||||||||||||
vB , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
2 , |
|
|
|
(6.3) |
||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
. |
|
(6.4) |
|||
|
|
|
|
BC |
AC |
|
AB |
|
||||||||||
Итак, в этом случае результирующее движение также является мгновенным вращением с аб-
189
Рис. 6.3.

солютной угловой скоростью |
1 2 (при |
условии 1 2 ) вокруг оси |
Cc , положение ко- |
торой определяется пропорцией (6.4). Легко проверить, что вектор суммарной угловой ско-
рости тела также можно определять по формуле
 1
1  2 .
2 .
Полученные результаты показывают, что векторы угловых скоростей тела, вращающегося вокруг параллельных осей, складываются независимо от их направлений этих скоростей.
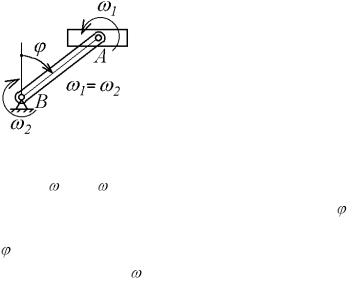
6.2.3. Пара вращений Рассмотрим частный случай, когда угловые
скорости тела вокруг параллельных осей направлены в разные стороны (рис. 6.3), а моду-
ли угловых скоростей равны 1  2 . Такая совокупность вращений называется парой вращений, а векторы 1 и 2 , образуют пару угловых скоростей (см. § 1.2). В этом случае по-
2 . Такая совокупность вращений называется парой вращений, а векторы 1 и 2 , образуют пару угловых скоростей (см. § 1.2). В этом случае по-
лучаем, что vA  2
2  AB , vB
AB , vB  1
1  AB , и vA = vB . Тогда (см. § 3.2) мгновенный центр скоростей
AB , и vA = vB . Тогда (см. § 3.2) мгновенный центр скоростей
тела будет находиться в бесконечности и все точки тела в данный момент будут иметь одинаковые скорости v 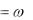

Следовательно, результирующее движение тела будет поступательным (или мгновенно по-
ступательным) движением со скоростью v , величина которой равна 1  AB , а направление перпендикулярно плоскости, проходящей через
AB , а направление перпендикулярно плоскости, проходящей через
|
|
|
|
|
векторы |
|
1 и |
|
2 ,. Направление вектора v оп- |
ределяется по правилу правого винта, то есть пара вращений эквивалентна поступательному (или мгновенно поступательному) движению со
190
скоростью v , равной моменту пары угловых скоростей этих вращений.
Рис. 6.4.
стей 1 и
Примером такого движения является поступательное движение велосипедной педали относительно рамы велосипеда (рис. 6.4), являющееся результатом относительного вращения педали вокруг оси А, укрепленной на кривошипе ВА, и переносного вращения кривошипа ВА вокруг оси В. Модули угловых скоро-
2 этих вращений равны, так как в
любой момент времени угол поворота 1 педали относительно кривошипа ВА равен углу поворота 2 кривошипа. Скорость поступательного движе-
ния педали v  2
2  AB .
AB .
§ 6.3. Цилиндрические зубчатые передачи
Механизмы, предназначенные для преобразования параметров движения, называются в технике передачами. Часть механизма, движущаяся как одно целое (не содержащая в себе других подвижных частей) называется звеном механизма. Звено может состоять из одной детали или нескольких неподвижно соединенных между собой деталей.
Условно неподвижное звено механизма называется стой-
кой.
Наиболее распространенными передачами являются механизмы, содержащие зубчатые колеса и называемые зубчатыми передачи.
Зубчатое колесо передачи, приводимое в движение каким либо двигателем или механизмом, называется входным.
191
Зубчатое колесо передачи, приводящее в движение какой либо другой механизм, называется выходным.
Все прочие зубчатые колеса зубчатой передачи называются промежуточными.
Полученные в предыдущем параграфе результаты могут быть использованы для кинематического расчета зубчатых передач, образованных цилиндрическими зубчатыми колесами. Рассмотрим основные виды этих передач.
6.3.1. Элементарные зубчатые передачи
Элементарной зубчатой передачей
|
называется механизм, |
|
состоящий из двух |
|
зубчатых колес и |
|
стойки. |
|
Передаточным |
Рис. 6.5. |
числом данной зубча- |
|
|
|
той передачи от коле- |
са k к колесу m называется величина ukn , равная отношению
модуля угловой скорости колеса k к модулю угловой скорости колеса m :
u |
|
k |
. |
(6.5) |
|
|
|||
|
km |
|
||
m
Передаточное число всегда положительно и может быть определено для любой зубчатой передачи при любой ориента-
ции векторов угловых скоростей |
k и m . |
|
|
Для передач с параллельными осями вращения зубчатых |
|||
колес можно определить передаточное отношение |
|
||
ikm |
k |
ukm , |
(6.6) |
|
|||
m
192
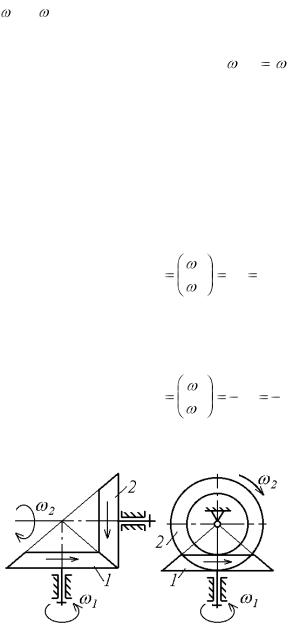
где знак «+» берется при одинаковых направлениях векторовk и m , а знак «-» берется в противном случае.
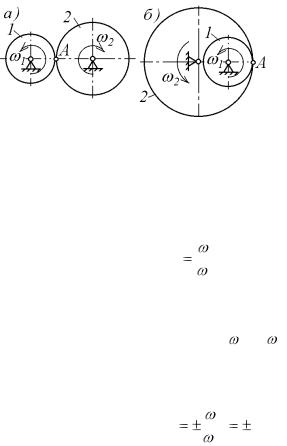
В случае внешнего (рис. 6.5, а) или внутреннего (рис. 6.5,
б) зацепления двух колес имеем |
1 |
r1 |
2 |
r2 , так как скорость |
точек зубьев, совпадающих в данный момент с неподвижной относительно стойки точкой А одинаковы.
Радиусы окружностей зубчатых колес, проходящих через точку А, пропорциональны числам z1 и z2 зубьев зацепленных колес.
При внутреннем зацеплении зубьев направления вращения колес (рис. 6.5, б) одинаковы, поэтому передаточное отношение такой передачи положительно и равно
i |
1 |
|
r2 |
|
z2 |
. |
(6.7) |
|
|
|
|
||||
12 |
|
|
r1 |
|
z1 |
|
|
|
2 |
|
|
|
|||
При внешнем зацеплении зубьев направления вращения колес (рис. 6.5, а) противоположны, поэтому передаточное отношение такой передачи отрицательно и равно
i |
1 |
|
r2 |
|
z2 |
. |
(6.8) |
|
|
|
|
||||
12 |
|
|
r1 |
|
z1 |
|
|
|
2 |
|
|
|
|||
Кроме рассмотренных зубчатых передач с параллельными осями вращения колес в технике широко используются конические зубчатые передачи (рис. 6.6), оси вращения колес которых пересекаются, и чер-
Рис. 6.6.
193
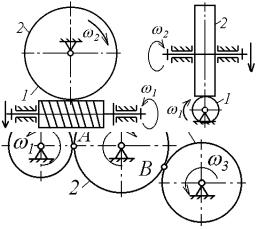
вячные передачи (рис. 6.7), оси вращения колес которых скрещиваются в пространстве обычно под прямым углом.
Для таких передач можно определить только передаточное число. Направление вращения выходного колеса удобно определять методом стрелок. Для этого на
Рис. 6.7. схеме зубчатого ханизма указывают стрелками либо направления линейных скоростей ближайших
к наблюдателю точек зубьев колес, либо угловых скоростей колес вращающихся относительно осей, перпендикулярных плоскости чертежа (см. рис. 6.5 и 6.6). Изображения стрелок ставятся с учетом действительных направлений вращения зацепляющихся зубчатых колес. Примеры применения метода стрелок показаны на рис. 6.5- 6.7.
Следует помнить, что звенья червячной передачи червяк
ичервячное колесо являются косозубыми зубчатыми колесами. Косозубое колесо может иметь правые или левые зубья. Зуб зубчатого колеса называется правым, если точка, движущаяся вдоль оси зуба и удаляющаяся от наблюдателя, вращается по ходу часовой стрелки. В противном случае зуб колеса
иколесо считаются левыми. При определении направления вращения червячного колеса по направлению вращения червяка следует учитывать направление зуба червяка. На рис 6.7 показана червячная передача с правым червяком.
6.3.2. Сложные зубчатые передачи
194
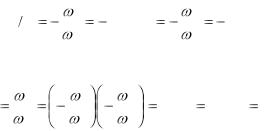
Передаточные числа элементарных зубчатых передач, за исключением червячных передач обычно не превосходят 10. Поэтому для получения больших передаточных чисел используются соединения элементарных пере-
дач, называемые сложными Рис. 6.8. (многоступенчатыми) зубчатыми
передачами.
Рядовой (обыкновенной) называется зубчатая передача, в которой все оси зубчатых колес неподвижны. В таких передачах одно из колес (например, колесо 1 на рис. 6.8) является входным, а остальные колеса могут быть промежуточными или выходными.
Существует два типа рядовых зубчатых передач: рядовая передача с паразитными колесами (рис. 6.8) и ступенчатая передача (рис. 6.9).
При внешнем зацеплении трех колес (рис. 6.8)
i |
1 |
|
r2 |
, i |
|
2 |
|
r3 |
. |
|
|
|
23 |
|
|
||||
12 |
|
|
r1 |
|
|
|
r2 |
||
|
2 |
|
|
3 |
|
||||
Передаточное отношение для всей передачи |
|||||||||
i |
1 |
|
1 |
|
2 |
i i |
|
z2 |
|
z3 |
|
z3 |
. |
|
|
|
|
|
23 |
|
|
|
|
||||
13 |
|
|
|
|
|
12 |
z1 |
|
z2 |
|
z1 |
||
|
3 |
2 |
3 |
|
|
|
|
||||||
Следовательно, передаточное отношение рядовой передачи с паразитными колесами равно отношению угловых скоростей крайних колес, обратно пропорционально их числам зубьев и не зависит от чисел зубьев промежуточных (паразитных) колес. Отсюда и происходит название паразитные колеса.
Легко проверить, что для сложной передачи с паразитными колесами, состоящей из n зубчатых колес, передаточное отношение
195
i |
( 1 )k |
zn |
( 1 )k |
rn |
i i |
|
....i |
|
, |
(6.9) |
|
|
23 |
1 )n |
|||||||
1n |
|
z1 |
|
r1 |
12 |
( n |
|
|
||
|
|
|
|
|
|
|
|
|
где k - количество внешних зацеплений в передаче.
Отличительной особенностью рядовой передачи с паразитными колесами заключается в том, что каждое колесо такой передачи вращается на отдельном валу или оси.
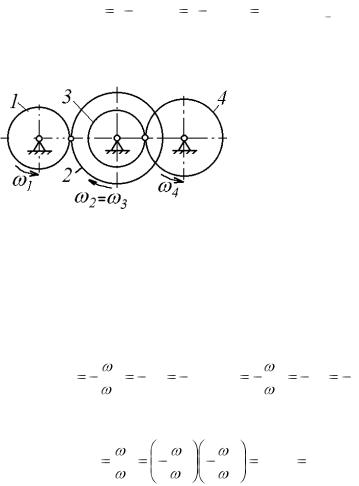
Рядовой ступенчатой называется зубчатая пере-
дача, в которой на некоторых валах могут вращаться более чем одно зубчатое колесо. Такие зубчатые колеса вращаются с одинаковыми угловыми скоростями.
Для элементарных передач, входящих в ступенчатую передачу, показанную на рис. 6.9, передаточные отношения
i |
1 |
|
r2 |
|
z2 |
, i |
|
3 |
|
r4 |
|
z4 |
. |
|
|
|
|
|
34 |
|
|
|
|
|
|||
12 |
|
|
r1 |
|
z1 |
|
|
r3 |
z3 |
||||
|
2 |
|
|
4 |
|
||||||||
Передаточное отношение для всей передачи |
|
|
|||||||||||
i |
1 |
|
1 |
|
3 |
i i |
z2 |
|
z4 |
. |
|
|
|
|
|
|
|
||||
14 |
|
|
|
|
|
12 34 |
z1 |
|
z3 |
|
|
4 |
2 |
4 |
|
|
|||||
Следовательно, передаточное отношение рядовой ступенчатой передачи равно отношению угловых скоростей входного и выходного колес зависит от чисел зубьев промежуточных колес.
Легко проверить, что для рядовой ступенчатой передачи, состоящей из n зубчатых колес, передаточное отношение
196
i |
i i |
|
....i |
|
( 1 ) |
k z2 |
|
z4 |
... |
zn |
|
, |
(6.10) |
|
23 |
1 )n |
|
|
|
|
|
|
|||||||
1n |
12 |
( n |
|
|
z1 |
|
z3 |
|
z( n |
|
|
|
||
|
|
|
|
|
|
|
|
|
1 ) |
|
|
|||
где k - количество внешних зацеплений в передаче.
6.3.3. Планетарные зубчатые передачи
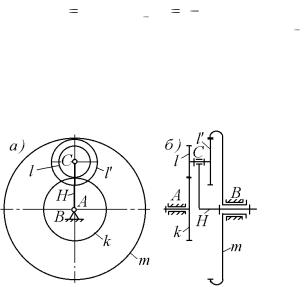
Планетарной называется зубчатая передача, в которой имеются зубчатые колеса, оси которых вращаются относительно подвижных осей. Зубчатые колеса планетарной передачи, имеющие
неподвижную ось вра- Рис. 6.10. щения, называемую
центральной осью, также называются центральными колесами (колеса k и m на рис 6.10). Зубчатые колеса планетарной передачи, имеющие подвижные оси вращения, называются сателлитами (колеса l и l на рис 6.10). Например, в передаче, изображенной на рис. 6.10, оси сателлитов l и l
на рис 6.10). Например, в передаче, изображенной на рис. 6.10, оси сателлитов l и l укреплены на рычаге Н, вращающемся вокруг центральной оси и называемым водилом.
укреплены на рычаге Н, вращающемся вокруг центральной оси и называемым водилом.
Планетарная передача, в которой все зубчатые колеса могут вращаться относительно своих осей, называется планетарной дифференциальной передачей. Если одно из центральных колес - k или m закрепить, то получится передача, называемая обыкновенной планетарной передачей.
Планетарные и дифференциальные передачи можно рассчитывать методом обращения движения или методом Виллиса, преобразующим планетарную зубчатую передачу в рядовую зубчатую передачу.
197
