Учебное пособие 1828

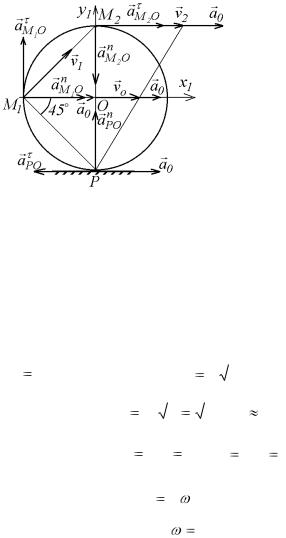
§ 3.4. Примеры решения задач

Пример 3.1. Колесо радиуса R = 1 м катится без скольжения по прямолинейному горизонтальному рельсу. Скорость и ускорение центра колеса в данный момент v0 = 1 м/с; a0 = 3 м/с2. Определить для данного момента времени скорости и ускорения

точек P, M1 и M2 колеса

(рис. 3.10).

Решение. Колесо движется плоскопараллельно. Берем за полюс центр О

колеса и применяем формулы (3.2) и 3.3). В соответствии с рис. 3.9 строим на рис. 3.10 для каждой из точек P, M1 и M2 составляющие векторов ускорений этих точек, а векторы скоростей тех же точек проводим перпендикулярно прямым, соеди-

Рис. 3.10. няющим эти точки с мгновенным центром скоростей

- точкой P. Скорость точки P равна нулю, так как по условию

Равенство (3.7) верно для каждого момента времени, а поэтому его можно продифференцировать по времени, учитывая

138

прямолинейно, его нормальное ускорение равно нулю (см. гл.

139

Решение. Из формулы (3.4) vA cos 30° = vB cos 60°; vB = 6

м/с. Мгновенный центр скоростей P находится на пересечении перпендикуляров AP и BP, идущих из точек А и В к векторам скоростей этих точек. Получаем равнобедренный треугольник

Из (3.5) следует, что скорость любой точки плоской фигуры равна ее расстоянию до мгновенного центра скоростей, умноженному на угловую скорость фигуры: vA = AP . Отсюда

vA / AP 2 с-1. По направлениям скоростей точек А и В

видно, что фигура (отрезок AB) вращается вокруг мгновенного центра скоростей против хода часовой стрелки.

Решим задачу другим способом. Проецируем (3.2) на направление AB и на перпендикуляр к AB. Из первого равенства

правлены противоположно, как скорости вращения относи-

Приняв направления по AB и по перпендикуляру к AB за оси х и у, спроецируем это равенство на эти оси

vDx 0,5( vA cos 30 vB cos 60 ) 3 м/с,

140

Пример 3.3. Отрезок AB = 1 м движется в плоскости чертежа. Ускорения концов A и В

даны: aA = 2 м/с2, aB = 2 м/с2 и образуют в данный момент с отрезком углы 90° и 45° (рис. 3.12). Определить для данного

Рис. 3.12. момента времени величины угловых скорости и ускорения отрезка.

Решение. Выбрав оси координат, и спроецировав равенство (3.3) на эти оси, получаем

Рис. 3.13. 141

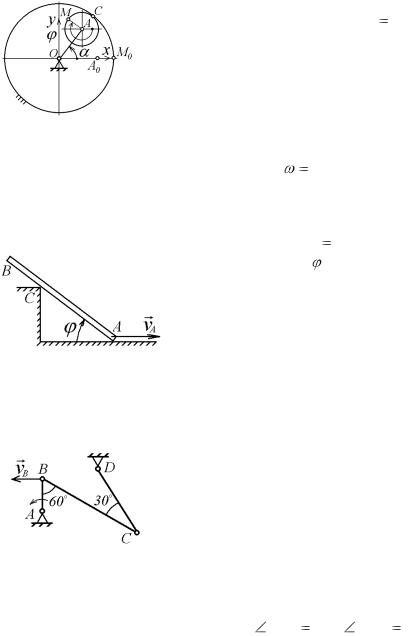
ОС, вращающимся равномерно вокруг оси О, с угловой скоростью const . Принимая точку А за полюс, составить уравнения движения линейки эллипсографа. Если ОС= ВС= АС= r .

3.2. Зубчатая шестерня радиуса r , катящаяся внутри неподвижного колеса

радиуса R (рис. 3.14), приводится в движение кривошипом ОА, вращающимся равномерно вокруг оси О этого колеса, с

подвижной шестерни, принимая ее центр А за полюс. Параметром считать время t . Считать, что правому горизонтально-

так, как указано на рисунке.

3.3. Стержень АВ длиной 5 м опирается на неподвижное ребро С двугранного угла (рис. 3.15) и дви-

жется в плоскости чертежа так, что его нижний конец А скользит по горизонтальной оси х со скоростью vA 4 м/с. Опреде-

лить угловую скорость и скорость Рис. 3.15. точек В и С стержня в момент, когда

угол 30 , если ОС= 2 м.

3.4. Кривошип АВ= 20 см совершает 120 оборотов в минуту и при помощи звена ВС= 100 см вращает стержень DC= 60 см, закрепленный шарнирно в точке D. Определить угловую скорость

стержня BC и угловую скорость стержня DC в момент, когда кривошип AB займет вертикальное положение. Известно, что в

(рис. 3.16).

142

нен шарниром стержень EВ= 80 см, который приводит в движение ползун В, перемещающийся по горизонтальной направ-

Определить ускорение ползуна В и угловое ускорение шатуна АВ в момент времени. Когда ABn 60 и АВ|| ОА (рис. 3.18).

3.7. В механизме, изображенном на рис 3.19, кривошип ОА = 25 см врашается с постоянной угловой скоростью = 2 с-1 в плоскости рисунка вокруг неподвижной точки О и при помощи стержня АВ приводит в движение кривошип ВС, вра-

143

щающийся в той же плоскости вокруг неподвижной точки С. Определить скорость и ускорение точки В в тот момент, когда

кривошип ОА горизонтален, ABC 30

АВ=ВС= 50 см.

3.8. В механизме, изображенном на рис. 3.20, кривошип ОА врашается в плоскости рисунка вокруг неподвижной точки О с угловой скоростью = 2 с-1 и угловым ускорением = 4 с-2 и приводит в движение свободно насаженную на него в точке А зубчатую шестерню 1 радиуса r1 = 5 см, катящуюся внутри неподвижного зубчато-

Рис. 3.20. го колеса 2 радиуса r2 = 15 см. Определить скорость и ускорение точки В подвижной шестерни, если

OAB 60 .

3.9. Равносторонний треугольник АВС движется в плоскости хОу так, что его вершины А и В перемещаются по

осям Ох и Оу, причем a A = 20 3 см/ с2, а aB = 20 см/ с2. Найти ускорение aC вершины С в момент времени, в кото-

3.22. Определить скорость и ускорение точки В.

144

3.11. Цилиндрический каток радиуса r катится без скольжения по цилиндрической лунке радиуса R так, что его центр С имеет постоянную по модулю скорость v . Определить

ускорение точки контакта катка А и диаметрально противоположной ей точки В.

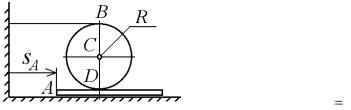
3.12. Пластина А перемещается по горизонтальной поверхности по закону sA( t ) 0,1( t4

м. На пластине находится каток радиуса R = 0,2 м, обмотанный

нерастяжимой нитью, конец Е которой закреплен на стене. Считая, что скольжение пластины по катку отсутствует, определить в момент времени t 0,5 с ускорения точек В, С и D катка, указанных на рисунке 3.23.

145

Глава 4. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА

§ 4.1. Движение твердого тела, имеющего одну неподвижную точку

Рассмотрим движение твердого тела, закрепленного так, что одна его точка О остается во все время движения неподвижной относитель-

но неподвижной системы отсчета Ox1 y1 z1 . Такое

движение совершает, например, волчок, у которого неподвижна только его опорная точка о плоскость, или любое другое тело, закрепленное в точке О шаровым шарниром.

Для определения положения тела в пространстве свяжем жестко с телом систему координат Oxyz , по положению которой можно судить о положении тела (рис. 4.1). Линия ОК, вдоль которой пересекаются плоскости Oxy и называется линией узлов.

Положение осей системы Oxyz относительно осей Ox1 y1 z1 , как и положение тела,

можно определить углами:

KOx , x1OK ,

z1Oz .

Эти углы называемые углами Эйлера, имеют следующие наименования, взятые из небесной механики: φ - угол собственного вращения, ψ - угол прецессии, θ - угол

нутации. Положительные направления отсчета

146

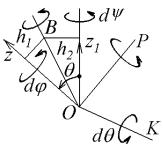
этих углов показаны на рис. 4.1 стрелками. При изменении угла φ тело совершает поворот вокруг оси Oz (собственное вращение), при изменении угла ψ – происходит поворот тела вокруг оси Oz1 (прецессия) и при изменении

угла θ – тело поворачивается вокруг линии узлов ОК (нутация).

Чтобы знать движение тела, надо знать его положение относительно осей в любой момент времени, т. е. знать зависимости:

f1( t ) , f2 ( t ), f3 ( t ) . (4.1)

Уравнения (4.1), определяющие закон движения тела, называются уравнениями движения твердого тела относительно

неподвижной точки.

Для определения структуры рассматриваемого движения, докажем следующую теорему Эйлера - Даламбера: всякое элементарное перемещение тела, имеющего неподвижную точку, является эле-

ментарным, поворотом вокруг некоторой мгновенной оси вращении, прохо-

дящей через эту точку.

Пусть положение тела определяется углами φ, ψ, θ. Тогда его перемещение за элементарный промежуток времени dt представится как совокупность поворотов на углы dφ, dψ, dθ вокруг осей Oz , Oz1 и ОК соответственно. Суммируясь, эти три поворота дадут истинное элементарное перемещение тела. Рассмотрим сначала, каким будет результат сложения поворотов

147