Учебное пособие 1828

ектории известна. Каток при движении катится без скольжения по конической поверхности К неподвижного катка.

Решение

Каток движется вокруг неподвижной точки О. Точки катка, лежащие на линии ОВ, должны иметь такие же скорости, как точки поверхности К, так как по ней каток катится без скольжения. Следовательно скорости этих точек равны нулю и линия ОВ является мгновенной осью вращения катка. Тогда vA h1 , где - угловая скорость катка при его повороте относительно оси ОВ; h1 - расстояние от точки А до этой оси.

Тогда vA / h1 .

где h2 - расстояние от точки С до оси ОВ.

Поскольку в рассматриваемом случае h2 2h1 , vC 2vA .

Скорость точки В, лежащей на мгновенной оси вращения равна нулю.

§4.5. Задачи для самостоятельного решения

4.1.Углы Эйлера, определяющие положение твердого тела с одной неподвижной точкой, из-

меняются по закону: , bt , c sin(0,5 t ), где

a , b и c - постоянные. Определить угловую скорость тела для момента времени t 1с.

158

4.2. Доказать, что если проекции абсоной угловой скорости тела на связанные с ним оси остаются постоянными, то движение тела является вращением с поянной скоростью относи-

но неподвижной оси.

4.3. Конический роликовый подшипник состоит из внутреннего кольца 1, насаженного на ось ротора 2, наружного кольца 3 и нескольких конических роликов. При указаных на рис.

Рис. 4.10. 4.10 размерах определить угловые скорость и ускоре-

ние ролика, если он катится без скольжения, а угловая скорость ротора постоянна.

4.4. Велосипедист движется по круговой дорожке трека с постоянной скоростью v . Радиус трека R , радиус колеса r ; принять, что во время движения плоскость колеса остается вертикальной и оно катится без скольжения. Каковы при этом угловая скорость и угловое ускорение колеса велосипеда?

4.5Определить в предыдущей задаче

углового ускорения колеса на х, у, z (ось х – направлена оси - вертикальна и проходит через

ось АВ, укрепленную в вилке 2, вращающейся вокруг вертикальной оси 3. При этом колесо

159

катится по горизонтальной поверхности без проскальзывания, касаясь ее одной точкой С. Определить модуль и направление ускорения центра колеса и точки касания его с поверхно-

160

Глава 5. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

§ 5.1. Относительное, переносное и абсолютное движения

До сих пор изучалось движение точки или тела относительно одной заданной системы отсчета. Однако при решении задач механики целесообразно, а иногда и необходимо рассматривать движение точки (или тела) одновременно относительно двух систем отсчета, из которых одна считается условно неподвижной, а другая определенным образом движется относительно первой. Движение, совершаемое при этом точкой (или телом), называется составным или сложным.

Например, шар, катящийся по полу движущегося вагона, можно считать совершающим относительно земли сложное движение, состоящее из качения относительно пола (подвижной системы отсчета) и движения вместе с полом относительно земли (неподвижной системы отсчета). Так сложное движение шара складывается из двух более простых и легко исследуемых движения. Возможность разложить более сложное движение точки или тела на более простые движения путем введения дополнительной (подвижной) системы отсчета широко используется в науке и определяет практическую ценность теории сложного движения. Кроме того, результаты этой теории используются в динамике для изучения относительного равновесия и относительного движения тел под действием сил.

Следует помнить, что движение по своей сути не может быть простым или сложным, поскольку является объективным процессом. Понятие сложного или простого движения появля-

161

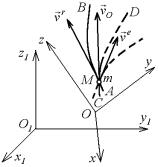
ется при попытке анализировать или описывать движение. Сложность или простота движения относительны, поскольку зависят от уровня знаний исследователя движения и выбора системы координат для описания движения.

Рассмотрим сложное движение точки М, перемещающейся относительно подвижной системы отсчета К (Oxyz ), которая в свою

очередь движется относительно другой системы от-

счета K1 (O1 x1 y1 z1 ) условно называемой неподвижной

(рис. 5.1). Каждая, из

Рис. 5.1. этих систем отсчета связана с определенным телом отсчета, не пока-

занным на чертеже.

Введем следующие определения:

1. Движение, совершаемое точкой М относительно подвижной системы координат K , называется относительным движением. Такое движение будет видеть наблюдатель, связанный с подвижной системой K (неподвижный относительно K ). Траектория АВ, описываемая точкой в относительном движении, называется относительной траекторией. Скорость движения точки М относительно системы K (т. е. вдоль этой кривой АВ) называется относительной скоростью

и обозначается r , а ускорение точки в этом v

движении - относительным ускорением и обозна-

неподвижной.

162

2. Движение, совершаемое подвижной системой отсчета K и всеми связанными с ней точками пространства относительно неподвижной системы K1 называется переносным движением.

Скорость связанной с подвижной системой K точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент и

обозначается e , а ускорение этой точки - пе- v

реносным ускорением точки М и обозначается ae . Таким образом,

где m – точка, неподвижная относительно системы K , с которой в данный момент совпадает движущаяся точка M.

Если представить, что относительное движение точки М происходит по поверхности (или внутри) твердого тела, с которым жестко связана подвижная система K , то переносной скоростью (или ускорением) точки М в данный момент будет скорость (или ускорение) той точки m тела, в которой в этот момент находится точка М.

3. Движение, совершаемое точкой относительно неподвижной системы отсчета K1 , назы-

вается абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью и обо-

значается v , а ускорение - абсолютным уско-

рением и обозначается a .

В приведенном выше примере движение шара относительно пола вагона будет относительным,

163

а скорость этого движения - относительной скоростью шара; движение вагона относительно земли будет для шара переносным движением, а скорость той точки пола, которой в данный момент касается шар, будет в

этот момент его переносной скоростью. Наконец, движение шара относительно земли будет абсолютным движением шара, а скорость этого движения - абсолютной скоростью шара.

§ 5.2. Сложение скоростей

Для определения зависимостей между относительными, переносными и абсолютными скоростями и ускорениями точки, рассмотрим сложное движение точки М. Пусть эта точка совершает за промежуток времени t t1 t вдоль своей относительной траектории АВ относительное пере-

мещение, определяемое вектором MM (рис. 5.2, а). Кривая АВ, двигаясь вместе с подвижной системой K (на рис. 5.2 оси K не показаны), перейдет за тот же промежуток времени в положение A1B1 .

Одновременно та точка m кривой АВ, с которой в момент t совпадает точка М, совершит

переносное перемещение mm1 Mm1 . В результате этих движений точка М придет в положение

Рис. 5.2. M1 и совершит за время t абсолютное перемещение MM1 .

Из треугольника Mm1M1 имеем:

164

MM1 Mm1 m1M1 .

Деля обе части этого равенства на t и переходя к пределу, получим

ным к соответствующим траекториям (рис. 5.2,

б).

Таким образом, доказана следующая теорема о сложении скоростей: при сложном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей. Построенная на рис. 5.2, б фигура называется параллелограммом скоростей.

Если угол между направлениями векторов e v

r

иv равен , то модуль вектора абсолютной скорости

165

v ( vr )2 ( ve )2 2vr ve cos .

С помощью параллелограмма скоростей решается ряд задач кинематики точки, а именно: а) зная скорости

найти модули этих скоростей; в) зная скорости

e

vи v , можно найти относительную скорость

точки v r из равенства

модулю и противоположным по направлению вектору v e .

§ 5.3. Сложение ускорений

Для определения зависимости между абсолютным, относительным и переносным ускорениями точки продифференцируем равенство (5.2)

соответственно необходимы выражения векторов v r , v e , a r , ae .

Пусть положение движущейся точки М в подвижной системе K определяется ее координата-

166

ми х, у, z (рис. 5.3).

Oxyz .

Дальнейшие выкладки зависят от характера переносного движения.

5.3.1. Сложение ускорений при поступательном

переносном движении

Если подвижная система отсчета K перемещается относительно неподвижной системы K1

поступательно (рис. 5.3), то очевидно, что при любом положении точки М будет

Кроме того, при поступательном движении системы K орты ее осей, перемещаясь параллельно самим себе, остаются постоянными. Тогда из (5.5) и (5.6) получим

167