Учебное пособие 1828
.pdf
1.5.3. Естественный способ
Формула (1.27) показывает, что ускорение точки характеризует изменение ее скорости. Величина и направление векто-
ра скорости v может меняться. Рассмотрим плоскую траекторию, имея в виду, что формулы, которые будут получены, верны и для пространственных траекторий.
Согласно (1.24) надо построить вектор |
|
|
|
||||
v приращения |
|||||||
|
|
вектора скорости. На |
|||||
|
|
рис. 1.11 изображены |
|||||
|
|
векторы скорости |
|||||
|
|
|
|
|
|
|
M1 A1 , |
|
|
v |
|
MA и v1 |
|||
|
|
соответственно для |
|||||
|
|
моментов времени t и |
|||||
|
|
t1. Для сравнения этих |
|||||
|
|
векторов построим |
|||||
Рис. 1.11. |
|
|
|
|
|
|
|
|
вектор v1 |
, отложив его |
|||||
|
M1 A1 |
|
|
|
|||
от точки M, т. е. перенесем вектор v1 |
параллельно в |
||||||
|
|
|
|
|
|
MB . Угол |
|
|
положение v |
||||||
|
|
|
|
|
|
|
|
|
|
между векторами v и |
|||||
|
|
|
|
|
|
|
|
|
v1 |
, называемый углом |
|||||
|
смежности, равен углу по- |
||||||
|
ворота касательной к тра- |
||||||
|
ектории при переходе по |
||||||
|
траектории от точки M к |
||||||
|
точке M1. По правилу век- |
||||||
|
торного сложения |
|
|||||
Рис. 1.12. |
MB |
MA |
AB , или |
||||
|
|
|
|
|
|
|
|
|
v1 |
= v |
+ |
v |
. Вектор прира- |
||
щения скорости v AB . |
|
|
|
|
|
|
|
Пусть v1>v (для случая v1<v построение аналогичное). От- |
|||||||
|
|
|
|
|
|
|
|
ложим вдоль вектора v1 |
MB отрезок MC = MA = v и предста- |
||||||
108
вим вектор приращения скорости |
|
виде суммы двух векто- |
v |
ров AB v AC CB . Треугольник AMC - равнобедренный. Из (1.27) имеем
|
|
|
|
|
|
|
|
|
|
a lim |
v |
lim |
AC |
CB |
lim |
AC |
lim |
CB |
. (1.32) |
|
|
|
|
|
|||||
t 0 |
t |
t 0 |
t |
t 0 |
t |
t 0 |
t |
||
Вектор ускорения точки состоит из двух векторов: нормального и касательного (тангенциального).
Касательным (тангенциальным) ускорением называют век-
тор
|
|
|
|
|
|
CB |
. |
|
|
|
|
|
|
(1.33) |
||
|
|
|
a |
lim |
|
|
|
|
|
|
|
|||||
|
|
t |
|
|
|
|
|
|||||||||
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
||
Так как при t |
0 |
|
|
0, то в пределе вектор CB , опре- |
||||||||||||
деляющий направление вектора |
|
|
|
|
|
|
|
|
|
|||||||
a , направлен по касательной |
||||||||||||||||
к траектории в точке M. Модуль этого вектора |
|
|
|
|
||||||||||||
|
|
CB |
|
| v1 |
v | |
|
| v | |
|
dv |
|
dv |
|
||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
a | a | lim |
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
. |
|
|
t |
|
|
t |
t |
|
dt |
|
dt |
||||||
t 0 |
|
t 0 |
|
|
t 0 |
|
|
|
||||||||
Итак, вектор касательного ускорения точки направлен по касательной к траектории, а его модуль равен модулю производной от модуля скорости по времени
|
|
dv |
|
dv |
|
|
a | a |
| |
|
|
|
. |
(1.34) |
dt |
dt |
|||||
Проекцией касательного ускорения на направление роста координаты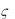 
называют производную от величины проекции скорости на то же направление по времени
a |
dv |
. |
(1.35) |
|
|||
|
dt |
|
|
109
Проекция скорости определяется формулой (1.24). Таким образом, величины v и a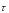
- алгебраические. По знаку a
нельзя судить, будет ли движение замедленным или ускоренным. Исходя из (1.24) и (1.35) легко установить, что при уско-
ренном движении точки знаки v и a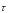
одинаковые ( v > 0, a
> 0 или v < 0, a
< 0), а при замедленном движении - разные
( v > 0, |
a < 0 или v < 0, |
a |
> 0). Очевидно, что при ускорен- |
|||||
ном движении точки направления вектора скорости v |
и каса- |
|||||||
|
|
|
|
|
|
|
|
|
тельного ускорения a |
совпадают, а при замедленном движе- |
|||||||
нии противоположны (рис. 1.12). |
|
|
|
|||||
Нормальным ускорением точки называют вектор |
|
|||||||
|
|
|
n |
|
|
AC |
. |
(1.36) |
|
|
|
a |
|
lim |
|
||
|
|
|
|
t |
||||
|
|
|
|
|
t 0 |
|
|
|
Направление |
вектора |
AC / |
t совпадает с направлением |
|||||
вектора |
AC , который составляет с касательной к траектории |
|||||||
угол |
90 |
/ 2 . При |
t |
0 |
|
90°. |
|
|
Следовательно, вектор нормального ускорения n направ- a
лен по нормали (перпендикуляру) к касательной к кривой к центру кривизны траектории в точке касания.
Модуль нормального ускорения
|
|
|
|
an |
lim |
AC |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
t 0 |
|
t |
|
|
|
|
|
|
Из |
MAC следует, что AC |
2v sin( |
/ 2 ) , |
|
|
|
|||||||
an |
lim |
AC |
lim |
2v sin( |
/ 2 ) |
|
lim |
v sin( |
/ 2 ) |
|
. |
||
|
|
|
|
|
|
|
|
|
|||||
|
t 0 |
t |
t 0 |
t |
|
|
|
|
t 0 |
( |
/ 2 ) |
t |
|
110
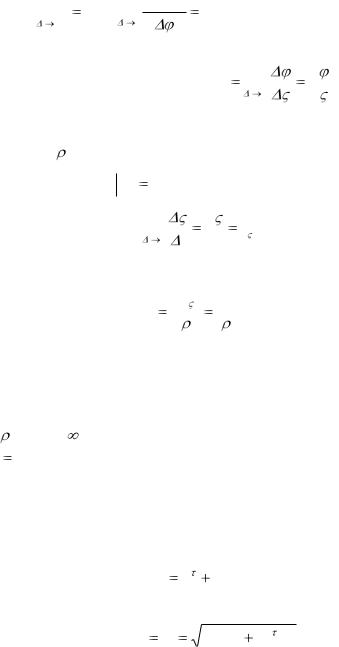
Но lim v v , а lim sin
1- первый замечательный
t 0 |
t 0 |
предел.
По определению, величина k lim |
|
|
d |
называется |
|
|
|
||
|
|
d |
||
t 0 |
|
|
|
|
|
|
|
|
кривизной траектории в точке М. Радиусом кривизны траектории в данной точке называют величину, обратную кривизне в этой точке =1/k.
Очевидно, что v
v . Согласно (1.21),
lim |
|
|
d |
v . |
|
|
|
||
t |
|
dt |
||
t 0 |
|
|
||
|
|
|
|
Тогда модуль вектора нормального ускорения
an |
v |
v |
|
v |
2 |
. |
(1.37) |
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
Итак, модуль вектора нормального ускорения точки равен отношению квадрата модуля линейной скорости точки к радиусу кривизны траектории.
Поскольку в любой точке прямой траектории кривизна k= 0, = 1/k= , т. е. радиус кривизны прямой бесконечен и an 0 .
Поскольку радиус кривизны окружности равен радиусу окружности, в любой точке окружности k = 1/R.
Вектор полного ускорения точки равен сумме векторов касательного и нормального ускорений этой точки
|
|
n |
. |
(1.38) |
a |
a |
a |
Из теоремы Пифагора (см. рис. 1.12) следует
|
(1.39) |
a | a | ( an )2 ( a )2 . |
111
Возможны следующие частные случаи.
Прямолинейное равномерное движение (инерциальное движение). В этом случае = , v= const. Отсюда (см. (1.35) и
(1.357)): an = 0; a
= 0; и поэтому а= 0. Итак, при прямолинейном равномерном движении точки ее ускорение равно нулю.
Прямолинейное неравномерное движение. Согласно (1.35)
и (1.37) |
|
|
и a= a |
= dv/dt. |
an = 0, поэтому a |
a |
При криволинейном движении с v= const a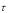
= d v /dt = 0;
|
n |
; а = a |
n |
2 |
a |
a |
|
= v / . |
Следовательно, касательное ускорение характеризует изменение величины скорости, а нормальное - изменение направления скорости.
Движение точки, при котором величина касательного ускорения постоянна a
= const, называют равнопеременным. От-
сюда, согласно (1.35) dv = a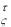
dt, после интегрирования полу-
чаем v = a
t + C1. Произвольную постоянную интегрирования можно определить из начального условия: при t0 = 0 v = v 0.
Имеем v 0 = C1, следовательно, v = v 0 |
+ a t. Учитывая (1.24) |
||||
и умножая на dt, находим d |
= v 0 dt + a |
t dt. |
|
||
После интегрирования получаем |
= |
v 0 t + a |
t2/2 + C2. |
||
Произвольную постоянную C2 определяем из начального усло- |
|||||
вия при t0 = 0, |
= 0. Тогда |
0 = C2 и |
|
|
|
|
= 0 + v 0 t + a |
t2/2. |
|
||
Итак, для равнопеременного движения |
|
|
|||
v |
v 0 a t; |
0 v 0t |
0,5a t 2 . |
(1.40) |
|
112
При решении задач почти всегда можно выбрать начало отсчета координаты 
так, что 0 = 0.
§ 1.6. Примеры решения задач
Пример 1.1. По окружности радиусом r = 9 м движутся в одном направлении две точки: M1 и M2; первая равноускоренно, а вторая равномерно со скоростью v2 = 6 м/с. В начальный момент обе точки находились в одном положении, причем скорость первой точки равнялась нулю. Найти, за какой промежуток времени первая точка догонит вторую и найти ускорения обеих точек в конце этого промежутка времени, если координаты точек будут равны 6 м.
Решение. Пусть для начального положения при t0 = 0 0 =
0. Для точки M1 v10 = 0 и, согласно (1.40), v |
a 1t и |
|
|
|
0,5a t 2 |
. Для второй точки, согласно (1.25), |
= v |
2 |
t. Обе |
1 |
|
|
|
|
точки в момент, когда первая догонит вторую, будут иметь координаты = 6 м в момент времени t = / v 2 = 1 с;
a 1 2
t 2 
12 м/с2. Скорость первой точки при t = 1 с v1=a
t= 12 м/с2. Нормальное ускорение первой точки a1n v12 
r 
16
м/с2. Согласно (1.39) a1 |
|
( a1n )2 ( a1 )2 20 м/с2. |
|
Величина ускорении точки M2 не зависит от времени, так |
|||
как при v = const a 2 |
dv2 |
0 , и величина полного ускорения |
|
dt |
|||
|
|
||
равна величине нормального ускорения а2 = аn2 = v22/r = 4 м/с2.
Пример 1.2. Движение точки задано уравнениями х = t2 и у = t - t3/3 (х, у - в м, t - в с). Найти траекторию и закон движения точки по траектории, отсчитывая расстояние от начального положения точки (при t0 = 0 0 = 0), а также найти скорость,
113
касательное, нормальное и полное ускорения и радиус кривизны траектории в момент времени t1 = 1 с.
|
Решение. В начальный мо- |
|
мент t0 = 0 с. Точка находилась |
|
в начале координат, так как по |
Рис. 1.13. |
заданным уравнениям движения |
x0 = 0, y0 = 0. Из уравнений движения исключаем параметр -
|
|
|
|
|
|
|
время t, t |
x , взяв положительное значение корня, так как по |
|||||
определению t 0. |
|
|
||||
|
|
|
|
|
|
|
Имеем y |
|
|
|
x |
|
( 3 x ), y 0 при x1 = 3 м и при x0 =0 . Легко |
3 |
|
|||||
|
|
|
||||
видеть, что при 0 < х < 3 у > 0. При x > 3, 3 - х < 0, и, следовательно, y < 0. На рис. 1.13 изображена траектория точки. Из
(1.22) и (1.23) следует
|
dx |
|
dy |
|
|
|
|
|
vx |
2t, vy |
1 t 2 |
; v |
vx2 v2y 1 t 2 . |
||||
|
|
|||||||
dt |
dt |
|||||||
|
|
|
|
|
|
|||
При t1 = 1 с v1 = 2 м/с.
Из (1.26) находим закон движения точки по траектории
|
|
|
|
t |
|
t |
|
|
|
t |
t |
|
|
||
|
OM |
|
v dt |
|
|
( 1 t 2 )dt |
dt |
t 2 dt t t 3 / 3 . |
|||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
0 |
|
|
|
Из (1.29) и (1.30) следует |
|
|
|
|
|||||||||||
|
|
d |
2 x |
|
|
|
|
|
d 2 y |
|
|
|
|
|
|
ax |
|
2м / с2 |
; ay |
2t м / с2 ; a |
4 4t 2 . |
||||||||||
|
dt2 |
dt2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
При t1 = 1 с a1 = 2 |
|
2 м/с2. |
|
|
|
|
|||||||||
Касательное ускорение находим по (1.35) |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
a |
|
dv |
2t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
114
При t1 = 1 с a1 =2 м/с2. Нормальное ускорение по (1.39)
a1n 
a12 ( a1 )2 
2 м/с2.
Радиус кривизны траектории по (1.37)
|
v2 |
|
|
|
1 |
2 м. |
|
1 |
an |
||
|
|||
|
|
||
|
1 |
|
Рис. 1.14.
Рис. 1.15.
мени t1 
3с.
§ 1.7. Задачи для самостоятельного решения
1.1. Линейка эллипсографа длиной АВ= l = 1 м скользит своими концами по осям Ох и Оу. Конец линейки А движется по оси Ох так, что ОА= 0,1 t м. Составить уравне-
ние движения точки В и определить скорости и ускорения точек А и В
(рис. 1.14).
1.2. Круглый эксцентрик диаметром 2 r вращается вокруг оси О, отстоящей от геометрической оси С эксцентрика на расстояние, равное ОС= a = r / 3 . Угол поворота эксцентрика изменяеется по закону
0,5 t , где угол измеряется в радианах,
r - в см, а t - в сек. Получить уравнение прямолинейного движения точки М стержня MN , движущегося в вертикальных направляющих (рис. 1.15), а также, скорость и ускорение точки в момент вре-
115
1.3. По заданным уравнениям движения точки в декартовых координатах найти траекторию, скорость и ускорение этой точки:
1) |
x |
0,5a( ekt |
e kt ) |
ach( kt ); |
y 0,5b( ekt e |
kt ) bsh( kt ) ; |
2) |
x |
R sin( t ); |
y |
R( 1 cos( 2 |
t )); z R sin( t ) , |
|
где координаты х, у, |
z заданы в метрах, время t |
- в секундах. |
||||
1.4. Составить уравнение движения точки М колеса трамвая, отстоящей от оси колеса на расстояние r = 0,8 м, если трамвай движется равномерно по прямолинейному участку пути со скоростью vC 
16 м/c, и найти скорость и ускорение
точки М. Колесо имеет радиус R 
1 м и катится по рельсу без
|
скольжения. В начальный мо- |
|
мент времени точка М |
|
мает нижнее положение на |
|
вертикальном диаметре ко- |
|
са. Начало системы координат |
|
расположить в точке контакта |
|
колеса с рельсом в начальный |
Рис. 1.16. |
момент времени. Ось х напра- |
вить в сторону движения колеса, ось у вертикально вверх.
1.5. Линейка эллипсографа длиной АВ= l = 10 
2 м скользит своими концами А и В по двум направляющим, обра-
зующим между собой угол 
135 . Найти траекторию, скорость и ускорение точки М линейки, если AM / BM 3 и закон движения ползуна А выражается уравнением ОА= s =
20 sin(0,5 t ) (рис. 1.16).
1.6.Вагонетка движется равномерно по закругленному
пути радиуса R 
600м, так, что ускорение ее некоторой точки равно a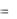 
0,0026 м/с2. Найти скорость этой точки вагонетки.
1.7.Точка движется с постоянным тангенциальным ускорением a по окружности радиуса R без начальной скорости. Через какое время после начала движения касательное и нормальное ускорения будут иметь одинаковые модули?
116
|
1.8. Точка движется по окруж- |
||||
|
ности. В некоторый момент времени |
||||
|
ее скорость стала равна v , а ускоре- |
||||
|
ние направлено по хорде MN l |
||||
|
(рис. 1.17). Найти ускорение точки в |
||||
|
этот момент. |
|
|
|
|
|
1.9. Автомашина идет по вы- |
||||
|
пуклому вверх мосту АВ (рис. 1.18). |
||||
|
Ее некоторая точка М описывает при |
||||
Рис. 1.17. |
этом параболу y |
0,005x |
2 |
, а рас- |
|
|
|
||||
|
стояние s |
AM , отсчитываемое от |
|||
|
точки А вдоль дуги параболы, изме- |
||||
|
няется по закону s |
( 2 / 3 )t 3 |
|||
|
9t 2 60t , где х и у выражены в |
||||
|
метрах, а время t - в секундах. Опре- |
||||
Рис. 1.18. |
делить скорость и ускорение точки М |
||||
|
в тот момент времени, когда она на- |
||||
ходится в вершине параболы, если в этот момент времени скорость машины достигает минимума.
1.10. Даны уравнения движения точки в декартовых координатах
x akt, x 0,5a( ekt e kt ) ach( kt ) .
Найти траекторию точки, закон движения точки по траектории и радиус кривизны траектории в зависимости от координаты у.
1.11. Даны уравнения движения точки x 2t , y 4t 2 ,
z 3t 2 , где координаты выражены в метрах, а время t – в секундах.
Найти радиус кривизны траектории в точке, где скорость
vточки равна 5 м/с.
1.12.От самолета, который летит со скоростью v0 на вы-
соте H над Землей, в некоторый момент времени отделяется
117