Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1828

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.34 Mб

Скачать

☆

<<< < Предыдущая 12 / 142 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

в зависимости от того, совпадает или нет направление вектора с положительным направлением оси.

Для положений, при которых = 90° или = 270°, из (1.4) следует Pl = 0, поскольку cos 90° = cos 270° = 0. Следователь-

но, если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.

При ручном решении задач, чтобы не применять формулы приведения из тригонометрии, лучше не брать косинусы углов, больших 90°, а всегда при вычислении проекции вектора умножать модуль вектора на косинус острого угла, образуемого вектором с прямой, параллельной оси l, а знак проекции определять по чертежу. Однако это правило нельзя применять при программировании решения задач теоретической механики для ЭВМ в тех случаях, когда величина угла между вектором и осью заранее не может быть оценена.

Из векторной алгебры известна теорема о проекции векторной суммы: проекция суммы векторов на какую-либо ось равна сумме проекций составляющих векторов на ту же ось

Rl= Pkl	(1.5)

здесь k - номер вектора; Рkl - проекция вектора Pk , на ось l.

Для обозначения проекций вектора Pk на оси координат используются следующие символы


npx Pk	( Pk )x Pkx	X k , npy Pk		( Pk )y Pky Yk ,
				Zk. .
	npz Pk	( Pk )z	Pkz	Zk. .

Приняв за оси для проецирования векторов координатные оси, согласно (1.5) получаем

Rx= Xk; Ry= Yk; Rz= Zk.

(1.6)

Из векторной алгебры известно, что проекции вектора определяют его величину и направление. Тогда

	R	R2	R2	R2 ,			(1.7)
		x	y		z
cos	Rx R ,	cos	Ry	R,	cos	Rz R,	(1.8)
				где	,	и - углы,		образо-
				ванные вектором			R	с ося-

ми координат.

						В дальнейшем понадо-
						бится так называемое пра-
						вило параллелепипеда, ко-
						торое	равносильно дву-
						кратному применению пра-
						вила параллелограмма.
						Из построения на рис.
					Рис. 1.6.	1.6 видно, что равнодейст-

						вующая	R трех векторов

P1	,	P2	,	P3	, приложенных в одной точке, приложена в той же

точке и равна по величине и направлению диагонали паралле-

лепипеда, ребра которого равны и параллельны указанным век-

торам. Согласно правилу параллелепипеда заданный вектор R можно разложить по трем заданным направлениям (осям) l1, l2, l3 единственным образом


R P1	P2	P3 .	(1.9)

Если составляющие векторы взаимно перпендикулярны, то получается прямоугольный параллелепипед.

При описании явлений в механике часто используется векторное произведение векторов. Векторным

	произведением двух векторов
	произведением двух векторов		a	и b
Рис. 1.7.
Рис. 1.7.	называют вектор c	, модуль которого
	называют вектор c	, модуль которого

численно равен площади параллелограмма, построенного на

векторах a и b , перпендикулярный к плоскости этого параллелограмма и направленный так, чтобы поворот на меньший

угол от			вокруг вектора		был виден происходящим про-
	a	к b		c

тив хода часовой стрелки, если смотреть в направлении, проти-


воположном направлению вектора		(рис.		1.7, а). Условное
воположном направлению вектора	c	(рис.		1.7, а). Условное
обозначение векторного произведения :						. Площадь
обозначение векторного произведения :			c	( a	b )	. Площадь

параллелограмма равна удвоенной площади одного из образующих параллелограмм треугольников.

Основные свойства векторного произведения следующие: 1) перестановка сомножителей векторного произведения

равносильно изменению направления вектора c на противоположное направление;

				(1.10)
( b	a )	( a	b ) ;	(1.10)

2) чтобы умножить векторное произведение на число, достаточно умножить на это число один из сомножителей

						(1.11)
( a	b )	( a	b )	( a	b ) ;	(1.11)

3) векторное произведение подчинено распределительному закону


( a	b ) c ( a			c ) ( b c ) .

При описании многих механических процессов используется понятие пары векторов и момента пары векторов.

В	некоторых случаях,	удобно	использовать		формулы,

выражающие проекции вектора c на оси некоторой системы

координат через проекции на эти оси векторов a				и b :
cx	aybz azby , cy azbx	axbz , cz	axby aybx .		(1.12)

Пара векторов Парой векторов, (или просто парой), называются два рав-

100

ных по модулю и противоположно направленных параллель-


ных вектора (рис. 1.8):	P	и	P	P . Расстояние h между ли-

ниями действий векторов, образующие пару, называется плечом пары векторов.

Момент пары векторов

Модулем момента пары векторов называют алгебраическое значение произведения модуля одного из векторов пары на плечо пары


m( P,P ) Ph .	(1.13)

Если плечо h представить твердым стержнем, а векторы пары считать силами, то при вращении стержня под действием сил пары против хода часовой стрелки момент пары векторов следует считать положительным, в противном случае момент пары векторов считается отрицательным.

Из рис. 1.8 следует

	(1.14)
\| m( P,P )\| Ph 2 пл ABD

т. е. модуль момента пары векторов равен удвоенной площади треугольника, основанием которого является один из векторов пары, а вершина находится в любой точке на линии, на которой находится второй вектор пары.

Рис. 1.8.		Свободным вектором называют
Рис. 1.8.	вектор, который можно, не меняя
	вектор, который можно, не меняя
его величины и направления, переносить параллельно.
Моментом пары векторов
Моментом пары векторов		m( P,P ) называют свободный

вектор, направленный перпендикулярно плоскости пары в ту сторону, чтобы, смотря в направлении, противоположном этому вектору можно было, видеть вращение пары против хода часовой стрелки. Модуль момента пары равен произведению

101

Рис. 1.9.

модуля одного из векторов пары на его плечо (рис. 1.8)

| m( P,P )| Ph 2 пл. OAB .

§1.3. Способы задания движения точки

Вкинематике независимой переменной (аргументом) является время t. Все другие величины – перемещения, координаты, скорости и ускорения являются функциями времени.

Механическим движением называют изменение с течением времени положения в пространстве точек и тел относительно какого-либо основного тела, с которым связана система отсчета. Кинематика изучает механическое движение точек и тел независимо от сил, вызывающих эти движения. Всякое движение, как и покой, относительно и зависит от выбора системы отсчета.

Траекторией точки называют линию, описываемую движущейся точкой. Если траектория - прямая линия, то движение точки называют прямолинейным, а если - кривая, то - криволинейным. Если траектория - плоская, то движение точки называют плоским. Движение точки или тела, считается заданным или

известным, если для каждого момента времени можно указать положение точки или тела относительно выбранной системы координат.

При изучении кинематики в зависимости от содержания задачи можно задавать движение точки следующими тремя способами.

102

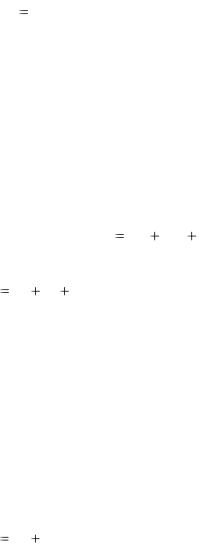
1.3.1. Векторный способ

Положение точки M определяется заданием векторарадиуса r этой точки как функции скалярного аргумента t

		(1.15)
r	r( t )	(1.15)

Модуль и направление вектора -радиуса r , имеющего начало в неподвижной точке О (полюсе) и конец в точке M, в общем случае меняется (рис. 1.9). Конец вектора - радиуса описывает траекторию точки M.

1.3.2. Координатный способ Выберем начало декартовых координат в начале вектора-

радиуса r . Координаты точки M -			конца r		- соответственно
равны проекциям r на оси координат:				rx = x; ry		= y; rz = z.

Пусть i , j ,k	-	единичные векторы осей координат. Тогда, век-

тор - радиус	r	можно записать в виде r		rxi	ry j	rz k или, в
данном случае,

		r xi yj zk .				(1.16)
Положение точки определяется тремя уравнениями движе-
ния в координатном виде
		х = х(t), у = у (t), z = z(t).				(1.17)

Эти выражения задают закон движения точки и являются уравнениями траектории в параметрическом виде. Для получения уравнения траектории в непараметрическом виде, надо из (1.17) исключить параметр - время t.

Если рассматривается плоская траектория, т. е. считается, что движение точки происходит в плоскости ху, то z= 0 и вместо (1.15) и (1.16) получаем

			(1.16’)
r	xi	yj ,	(1.16’)
х = х(t), у = у (t).			(1.17’)

103

1.3.3. Естественный способ

Положение точки в пространстве определяется заданием: а) траектории точки; б) криволинейной координаты = O1M

точки М, отсчитываемой вдоль траектории и начала O1 ее отсчета (см. рис. 1.9); в) направления положительного отсчета координаты ; г) уравнения или закона движения точки по траектории

=(t). (1.18)

§1.4. Скорость точки

Взависимости от способа задания движения скорость точки выражается в трех различных видах.

1.4.1. Векторный способ

Мгновенной скоростью точки называют вектор v , равный первой производной от вектора - радиуса точки по времени

(1.19)

lim

t 0

На рис. 1.10 моменту

времени

t соответствует

вектор-

радиус r , моменту t1 = t +

t - вектор -радиус r1

r , где

приращение

вектора -

радиуса

MM 1 .

(перемещение) r

Вектор

r ,

как

произведение

вектора

на

число

направлен по вектору

r .

Рис. 1.10.

При

0 вектор

будет по-

ворачиваться вокруг точки M, и так как в пределе секущая MM1 к кривой, когда расстояние между точками M и M1 стре-

104

мится к нулю, превращается в касательную, то получаем, что

вектор скорости v направлен по касательной к траектории в сторону движения точки.

1.4.2. Координатный способ

Представляя r в виде (1.16), подставляя r в (1.19) и, учитывая, что единичные векторы, как постоянные вектоы, выно-

сятся за знаки производных, получаем

k .

(1.20)

Как и любой вектор, вектор скорости точки может быть

представлен в виде суммы

vx i

vy j

vz k .

(1.21)

Следовательно,

; vy

;

(1.22)

Итак, проекция вектора скорости точки на неподвижную ось координат равна первой производной по времени от соответствующей координаты точки.

Модуль и направление вектора скорости определяются формулами


			vx2 vy2	vz2 ,
v	v		vx2 vy2	vz2 ,		cos( v ,x )
				vy
		cos( v , y )			,	cos( v ,z )
		cos( v , y )		v	,	cos( v ,z )

	vx ,
	v
	vz	(1.23)
	v	(1.23)
	v

1.4.3. Естественный способ По определению скорость точки направлена по касатель-

ной к траектории, а ее проекция на вспомогательную ось задается формулой

105

v	d	(1.24)

	dt .

Размерность скорости точки: [ v ] длина / время, например м/с. Если точка движется в сторону увеличения криволи-

нейной координаты		, то d		> 0, и, следовательно, v				> 0. В
противном случае d	< 0 и v			< 0.
Движение точки называют равномерным, если величина
скорости постоянна	v		d	const .		Отсюда d	= v	dt. Ин-

			dt

тегрированием получаем
d		v dt		v	dt;	v t	C.
Выбираем начало отсчета O1					на траектории так, чтобы при

t0 = 0 0 = 0. Из последнего равенства находим произвольную

постоянную интегрирования C = 0. Тогда		= v	t или
v	/ t .		(1.25)
Из (1.24) d = v dt. Интегрирование дает
t
	v dt .		(1.26)
0
Полученная формула позволяет найти закон движения в
виде (1.18), если известна зависимость v		= v	(t).

§ 1.5. Ускорение точки

Ускорение точки, так же как ее скорость, в зависимости от способа задания движения определяется следующими способами.

106

1.5.1. Векторный способ.

Ускорением точки называют вектор a , равный первой производной от вектора скорости точки по времени


		v	dv	.	(1.27)
a	lim
a	lim	t	dt
	t 0	t	dt

Размерность ускорения в СИ [а] = м/с2, а единицей измерения является 1 м/с2.

1.5.2. Координатный способ Согласно (1.27) и (1.21)

		dvx		dvy		dvz
	dv
a			i		j		k .

	dt	dt		dt		dt

Поскольку a

axi

ay j

az k , получается

;

dvy

;

(1.28)

Учитывая (1.22), получаем

d 2 x

;

d 2 y

;

2 z

(1.29)

dt2

Итак, проекции вектора ускорения точки на неподвижные оси координат равны вторым производным по времени от соответствующих координат точки. Модуль и направление вектора ускорения точки

cos( a,x )

		ax2 a2y
\| a \|		ax2 a2y
ax
	, cos( a, y )
a	, cos( a, y )
a

az2 ,			(1.30)
ay		az	. (1.31)
	, cos( a,z )
a	, cos( a,z )	a
a		a

107

<<< < Предыдущая 12 / 142 3 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20222.31 Mб5Учебное пособие 1823.pdf
#
30.04.20222.31 Mб2Учебное пособие 1824.pdf
#
30.04.20222.32 Mб4Учебное пособие 1825.pdf
#
30.04.20222.32 Mб7Учебное пособие 1826.pdf
#
30.04.20222.34 Mб13Учебное пособие 1827.pdf
#
30.04.20222.34 Mб6Учебное пособие 1828.pdf
#
30.04.20222.35 Mб6Учебное пособие 1829.pdf
#
30.04.2022315.72 Кб3Учебное пособие 183.pdf
#
30.04.20222.35 Mб3Учебное пособие 1830.pdf
#
30.04.20222.36 Mб6Учебное пособие 1831.pdf
#
30.04.20222.36 Mб2Учебное пособие 1832.pdf