Учебное пособие 1828

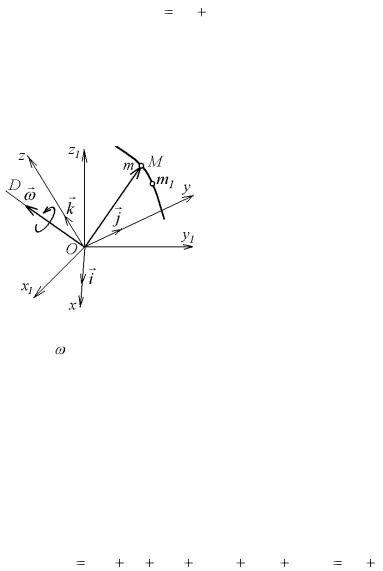
В результате формула (5.4) дает

Следовательно, при поступательном переносном движении абсолютное ускорение точки равно векторной сумме относительного и переносного ускорений. Получен результат, аналогичен тому, который дает теорема о сложении скоростей.

5.3.2 Сложение ускорений при непоступательном

переносном движении. Теорема Кориолиса

Допустим сначала, что переносное движение (т. е. движение подвижной системы отсчета

Oxyz ) является вращательным с угловой скоро-

стью (рис. 5.4). При этом ось OD может быть или неподвижной, или мгновенной осью вращения (когда неподвижна точка О, см. § 4.1). В обоих случаях орты i, j, k уже не яв-

ляются постоянными, так как, поворачиваясь вместе с осями Oxyz , они изменяют свои направле-

ния, что при опрделении r не учитывалось. w

Поэтому из равенств (5.5), применимых к любому переносному движению, получим

вой части последнего равенства.

168

Из формул Пуассона (§4.3) следует

Далее, при вращательном движении скорость и ускорение любой жестко связанной с системой K точки m определяются по формулам (4.3) и (4.5), как и для точек твердого тела. Соглас-

где r - вектор -радиус- точки m, совпадающий в данный момент времени с вектором - радиусом движущейся точки M относительно системы K .

Тогда

Поскольку стоящая слева производная входит в правую часть равенства (5.4), определяющую абсолютное ускорение точки M, т. е. ее

169

свой вид, с той лишь разницей, что в (5.10)

величина e будет определяться не по формуле a

(5.9), а по формуле (4.10).

Подставляя теперь величины (5.8) и (5.10) в (5.4), получим

(5.12)

Величина k , характеризующая изменение a

вектора относительной скорости r в перенос- v

ном движении и вектора переносной скорости e v

в относительном движении, называется поворотным или кориолисовым ускорением точки. Тогда (5.11) примет вид

(5.13)

Эта формула выражает следующую теорему Кориолиса: абсолютное ускорение точки равно векторной сумме трех ускорений: относительного, характеризующего изменение относительной скорости точки в относительном движении, переносного, характеризующего изменение переносной скорости точки в переносном движении, и кориолисова ускорения, характеризующего изменение относительной скорости точки в переносном движении и переносной скорости точки в относительном движении.

Если переносное движение является посту-

171

пательным, то = 0 и k = 0, и (5.13) пе- a

реходит в (5.7).

5.3.3. Определение относительного, переносного

и кориолисова ускорений Методы определения относительного и пере-

носного ускорений точки были, рассмотрены при доказательстве теоремы. Эти ускорения определяются по известным формулам кинематики.

ся обычными методами кинематики точки (§§1.4,

1.5).

При определении же e не надо учитывать a

относительное движение точки. Следовательно,

e нужно определять методами кинематики твер- a

дого тела (§§ 4.2, 4.4), как ускорение точки некоторого твердого тела, неизменно связанного с системой K и движущегося вместе с этой системой.

Кориолисово ускорение определяется по формуле (5.12):

ak 2( v r ), (5.14)

где - угловая скорость переносного движения.

Таким образом, кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную скорость точки.

172

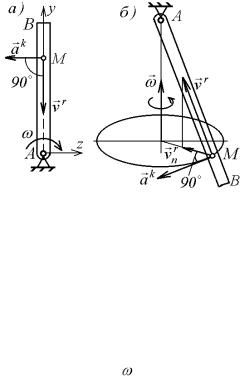
рону переносного вращения. Если относительная траектория – плоская кривая и перемещается все время в своей плоскости, то угол = 90° (рис. 5.5, б), и в этом случае

(5.16)

Как видно из рис. 5.5, б, направление k a

можно найти, повернув вектор относительной

скорости r на 90° в сторону переносного вра- v

щения (т. е. по ходу или против хода часовой

173

стрелки, в зависимости от ния вращения). В

этом заключается правило Н.Е. Жуковского.

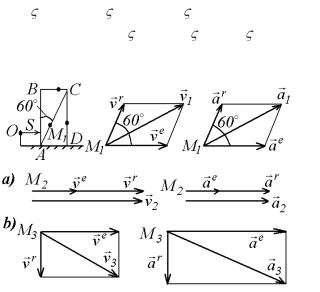
На рис. 5.6 для иллюстрации приведенных правил показано направление вектора корио-

лисова ускорения шарика М, движущегося вдоль трубки АВ в случаях, когда трубка вращается в плоскости чертежа (рис. 5.6, а) и когда она при вращении описывает конус (рис. 5.6, б).

Из формулы (5.15) видно, что кориолисово Рис. 5.6. ускорение может обращаться в нуль в следующих случа-

ях:

1)Когда = 0, т. е. когда переносное движение является поступательным (формула 5.7), или если угловая скорость переносного вращения в данный момент времени обращается в нуль.

r

2)Когда v = 0, т. е. когда относительная скорость в данный момент времени обращается в нуль.

3)Когда = 0, или =180°, т.е. когда относительное движение происходит по направлению, параллельному оси переносного вращения

или если в данный момент времени вектор r v

параллелен этой оси.

174

§ 5.4. Примеры решения задач

А. Переносное движение поступательное

В случае, когда переносное движение является поступательным, характер задач и методы их решения аналогичны задачам на сложение скоростей (§ 5.2).

Пример 5.1. Прямоугольная пластина ABCD (рис. 5.7) движется поступательно, причем ее расстояние от неподвижной точки О изменяется согласно закону = 3t + 3t3 (t - в с,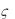

- в м).

По диагонали AC, составляющей угол 60° со стороной AD и по сторонам пластины движутся три точки так, что расстоя-

Определить в момент времени t1= 1 с абсолютные скорости и ускорения точек M1,

M2, M3.

Решение. Подвижную систему координат мысленно скрепляем с пластиной. Оси координат перемещаются параллельно, т. е. движутся

Рис. 5.7. поступательно. Непод-

вижная система отсчета скреплена с плоскостью, по которой скользит пластина. Применим формулы (3.1) и (3.2). Так как при поступательном движении твердого тела скорости и уско-

175

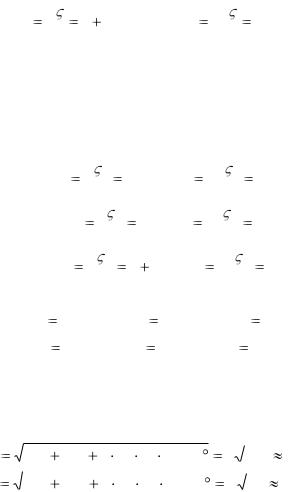
рения всех его точек соответственно равны между собой в каждый момент времени, то, скрепив мысленно точки M1, M2 и M3 с подвижной системой координат, т.е. с пластиной, получаем, согласно определению переносного движения, что переносные скорость и ускорение точек M1, M2 и M3 равны соответственно скорости и ускорению какой-нибудь точки пластины, например точки А. Все точки пластины движутся прямолинейно, и поэтому скорости и ускорения этих точек направлены вдоль их прямолинейных траекторий

При t1 = 1c ve 1 = 12 м/с; ae 1 = 18 м/с.

Относительным движением точек M1, M2, M3 являются их прямолинейные движения по пластине, и поэтому относительные скорости и ускорения этих точек направлены вдоль их прямолинейных относительных траекторий, т. е. по отрезкам

AC, ВС и CD

Согласно (3.1) и (3.2) строим параллелограммы скоростей и ускорений (см. рис. 5.7). Модули полученных векторов находим по теореме косинусов

176

Пример 5.2. Клин, движущийся горизонтально с ускоре-

нием a1 перемещает вдоль вер-

тикальных направляющих стержень АВ (рис. 5.8). Опреде-

лить ускорение стержня aA , если угол клина равен .

Решение. Абсолютное ускорение aA , точки А стержня направлено вертикально вверх. Его можно рассматривать как состоящее из относи-

тельного ускорения r , направленного вдоль a

наклонной плоскости клина, и переносного ус-

корения e , равного ускорению клина, посколь- a

ку переносное движение, т.е. движение клина, является при этом поступательным. Строя в соответствии с равенством (5.7) параллелограмм

ускорений и учитывая, что

Вектор aA и определяет ускорение стержня.

Б. Переносное движение вращательное

Рассмотрим определение a в общем случае, когда переносное движение является вращением вокруг некоторой неподвижной

оси.

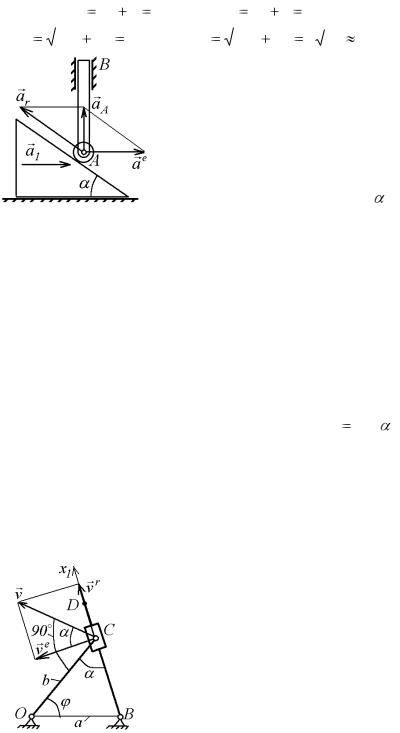
Пример 5.3. Кулисный механизм с качающейся кулисой приводится в движение кривошипом ОС (рис. 5.9). Определить скорость движения точки С пол-

177