
Учебное пособие 1828
.pdf
2.7. Зубчатое колесо 1 с числом зубьев z1  80 начинает вращаться
80 начинает вращаться
но из состояния покоя с угловым ускорени-
ем |
1 |
1 с-2 |
и приводит в движение нахо- |
|
|
|
дящееся с ним во внутреннем зацеплении колесо 2 с числом зубьев z2 = 20 (рис. 2.6).
Определить угловую скорость колеса 2 и ускорение точки В, лежащей на окружности этого колеса через 1 с после начала
|
движения, если радиус колеса 2 r2 15 см. |
Рис. 2.6. |
2.8. Устройство, подающее детали в |
печь для просушивания (рис. 2.7), состоит из кривошипа ОА, вращающегося в вертикальной плоскости, и соединенного с ним шарнирно стержня АВ с поддоном. Во время движения устройства стержень АВ вертикален. Определить зависимость
|
угла поворота криво- |
|
|
шипа ОА от времени при |
|
|
условии, что скорость |
|
|
транспортируемого груза в |
|
|
поддоне была постоянна и |
|
Рис. 2.7. |
равна 0,05 м/c. Найти также |
|
уравнение траектории точки |
||
|
В, если АВ= 0,8 м, ОА= 1,5 м. Считать, что в
начальный момент времени |
0 . |
2.9.В механизме, изображенном на рис.
2.8.точка А, находящаяся в на середине звена ВС (шатуна), движется равноускорен-
но. Касательное ускорение этой точки a
 5 м/с2. Длина звена ВС = 1 м, а кривошипа ОВ= DС= 50 см. В начальном положении стержень ОВ горизонтален, а угловая скорость его равна 0. Найти уравнение траектории точки А, угловую скорость и
5 м/с2. Длина звена ВС = 1 м, а кривошипа ОВ= DС= 50 см. В начальном положении стержень ОВ горизонтален, а угловая скорость его равна 0. Найти уравнение траектории точки А, угловую скорость и
угловое ускорение кри-
Рис. 2.8. |
вошипа, скорость и уско- |
|
|
рение точки В. |
|
128

2.10. Зубчатая рейка 1 (рис. 2.9) движется в горизонтальных направ-
ляющих по закону s at3 м из состояния покоя и приводит во вращение шестерни 2 и 3. С шестерней 3 жестко связан барабан, на который наматывается нерастяжимая нить с грузом В на конце. Найти скорость и ускорение гру-
за, если радиусы шестерни 3 и барабана равны между собой.
Рис. 2.9. |
2.11. ―Колесо обозрения‖ (рис. |
|
2.10) вращается вокруг горизонтальной |
||
|
оси О в вертикальной плоскости. В точке А к нему подвешена шарнирно кабина В, которая движется поступательно. Найти максимальную перегрузку в вертикальном направлении
|
|
n |
ay |
/ g , испытываемую человеком, |
|||
|
|
находящемся в кабине, если колесо вра- |
|||||
|
|
щается равномерно с угловой скоростью |
|||||
|
|
. Здесь g - ускорение свободного па- |
|||||
|
|
|
|
||||
|
|
дения; |
ay |
- проекция ускорения челове- |
|||
|
|
ка на вертикальную ось. |
|||||
|
|
|
2.12. В цилиндрической зубчатой |
||||
|
|
|
|
|
|
|
передаче находят- |
|
|
|
Рис. 2.10. |
ся в зацеплении |
|||
|
|
|
|
|
|
|
два зубчатых колеса |
|
|
|
|
|
|
|
радиусов r1 и r2 . |
|
|
|
|
|
|
|
Найти скорости и |
|
|
|
|
|
|
|
ускорения двух со- |
|
|
|
|
|
|
|
прикасающихся то- |
|
Рис. 2.11. |
чек колес M 1 и M 2 |
в момент времени |
||||
|
|
||||||
t1 |
/ 3 с после начала движения, если первое колесо вра- |
||||||
щается по закону 1 sin |
t рад и r1 / r2 = 2. Положение меха- |
||||||
низма изображенное на рис. 2.11, соответствует времени t1 .
129

Глава 3. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
§ 3.1. Плоскопараллельное движение
Плоскопараллельным, или плоским, называют движение твердого тела, при котором существует такая неподвижная плоскость P, что расстояние от любой точки тела до этой плоскости во время движения не изменяется (рис. 3.1). Из этого определения следует, что всякий отрезок прямой Lk M k , связанный с телом,
перпендикулярный плоскости P перемещается поступательно, и поэтому все точки этого отрезка движутся одинаково. Если проведем плоскость Q параллельно плоскости P так, чтобы она пересекала тело, то получим плоскую фигуру S, по движениям точек которой можно определить движения всех точек тела. Например, точка Ак в плоскости Q будет двигаться так же, как и все точки отрезка Lk M k . Плоская фигура S будет двигаться в плоскости Q. Сле-
довательно, изучение плоскопараллельного движения тела сводится к изучению движения его сечения - плоской фигуры S в своей плоскости Q (плоскость ху).
Изучение плоского движения тела имеет важное прикладное значение, так как почти все части большинства механизмов и машин совершают плоскопараллельное движение.
|
Возьмем на плоской фигуре S |
|
произвольную точку А (полюс) и |
|
примем ее за начало поступательно |
|
движущейся системы координат |
Рис. 3.2. |
Аx1y1 (рис. 3.2). Эти оси связаны с |
|
130 |

фигурой S так, что имеют с ней одну общую точку - полюс А. Можно представить себе, что через точку А проходит ось вращения фигуры относительно подвижных осей Аx1 и А1y1 системы координат, которые остаются соответственно параллельными неподвижным осям Ox и Oy. Если плоскую фигуру S мысленно скрепить с подвижными осями, то она будет двигаться вместе с ними поступательно.
|
Для выяснения сущности плос- |
|
|
копараллельного движения рассмот- |
|
|
рим два положения 1 и 2, которые |
|
|
заняло сечение тела S в моменты |
|
|
времени t1 и t2 t1 t (рис. 3.3). |
|
|
Очевидно, что сечение S, а с ним и |
|
|
все тело, можно перевести из поло- |
|
|
жения 1 в положение 2 в два приема. |
|
|
Сначала можно перенести тело по- |
|
|
ступательно, так, чтобы полюс А |
|
Рис. 3.3. |
двигался по его траектории из точки |
|
A1 в точку A2 . При таком движении |
||
|
отрезок А1В1, двигаясь параллельно самому себе, переместится в положение A2 B2 . Затем следует повернуть сечение S вокруг полюса А2 на угол , отсчитанный от отрезка A2 B2 . Рассмотренные движения можно реализовать и в обратном порядке.
Отсюда следует, что плоскопараллельное движение твердого тела можно считать состоящим из поступательного движения, при котором все точки тела движутся так же, как и полюс, и вращательного движения тела относительно этого полюса.
Оба составляющих движения происходят одновременно и в результате, как будет доказано ниже, образуют в каждый момент времени вращательное движение вокруг особой точки - мгновенного центра скоростей, неподвижной в данный момент времени относительно неподвижной системы Оху.
131

Поступательная часть движения плоской фигуры S характеризуется поступательным движением одной из точек тела, например полюса А, и определяется уравнениями: x01 = x01(t), y01 = y01(t). Отрезок АВ за время t поворачивается вместе с фигурой S вокруг полюса А (относительно подвижной системы координат) на некоторый угол . Вращение плоской фигу-
ры S относительно полюса А определяется функцией |
= (t). |
Уравнениями (законом) плоскопараллельного движения |
|
тела называют уравнения |
|
x01 = x01(t), y01 = y01(t), = (t). |
(3.1) |
Очевидно, что если взять за полюс некоторую другую точку С сечения S и провести из полюса С параллельно отрезку АВ отрезок СD, то за время t он повернется на тот же угол , что и отрезок АВ, так как эти отрезки по построению остаются все время параллельными друг другу. Таким образом, угол поворота плоской фигуры вокруг любого полюса не зави-
сит от выбора этого полюса.
§ 3.2. Скорости точек тела в плоскопараллельном движении
Поскольку угол поворота плоской фигуры вокруг любого полюса не зависит от выбора этого полюса, угловые
скорость |
d |
и ускорение |
d |
|
|
|
|||
dt |
dt |
|||
|
|
|
плоской фигуры в ее вращении вокруг |
|
Рис. 3.4. |
полюса не зависят от выбора этого по- |
|
люса. |
||
|
Положение некоторой точки В сечения S относительно
|
|
|
|
|
точки О определяется вектор - радиусом r |
rA |
|
r , где |
rA |
вектор – радиус точки А относительно точки О, а |
r |
- вектор – |
||
радиус точки В относительно точки А. По определению скорости
132

|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dr |
|
drA |
|
dr |
. |
|
||||||
vB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
dt |
|
dt |
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
В |
|
|
этом выражении вектор |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
drA |
|
|
характеризует |
изменение |
||||||||
|
|
|
|
|
|
|
vA |
|||||||
|
|
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
вектора |
в системе координат Оху и |
||||||||||||
|
rA |
|||||||||||||
|
определяет скорость полюса А в этой |
|||||||||||||
|
системе |
|
координат. |
Величина |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dr |
|
|
характеризует |
изменение |
||||||||
|
|
|
|
|
|
|
vBA |
|||||||
|
|
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
вектора |
в системе координат Ах1у1 |
||||||||||||
Рис. 3.5. |
r |
|||||||||||||
и определяет скорость точки В относительно точки А, то есть скорость точки В относительно полюса (рис.3.5).
Следовательно vB vA vBA .
Итак, скорость любой точки тела, совершающего плоское движение можно представить в виде векторной суммы вектора скорости полюса и вектора скорости этой же точки относительно полюса.
При вращательном движении vBA AB , и согласно (2.9) vBA=AB .
.
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
vB |
vA |
vBA |
; vBA |
AB; vBA |
AB . |
(3.2) |
Спроецировав векторное равенство (3.2) на отрезок AB, и |
||||||
|
|
|
|
|
|
|
учитывая, что vBA |
AB получим npAB vBA |
0 . Тогда |
|
|||
|
|
|
|
|
|
|
|
|
npAB vB |
npAB vA . |
|
(3.3) |
|
Проекции скоростей любых двух точек плоской фигуры, движущейся в своей плоскости, на прямую, соединяющую эти точки, равны. Это утверждение верно только для абсолютно
133

твердого тела, поскольку в деформируемом теле точки А и В могут двигаться друг относительно друга за счет деформаций.
3.2.1. Мгновенный центр скоростей
Введем произвольный подвижный элемент плоскости, связанный с плоской фигурой S.
Теорема 3.1. В каждый момент времени, когда угловая скорость плоской фигуры, движущейся в своей плоскости, не равна нулю, в плоскости фигуры существует точка P, называемая мгновенным центром скоростей, скорость которой в этот
Рис. 3.6. момент равна нулю.
Доказательство. Построим вектор AP произвольной длины, направленный также, как и повернутый на 90° в сторону
вращения фигуры S вектор скорости |
|
точки А (рис. 3.6). То- |
||||||||
vA |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
гда v |
vA |
vPA , |
vPA |
AP и vPA |
AP |
|
. Векторы vA |
и |
vPA |
на- |
правлены по одной прямой в противоположные стороны, а поэтому величина скорости точки P будет равна vP vA AP  .
.
Пусть расстояние AP таково, что vP |
0 . Тогда |
AP vA / . |
(3.4) |
|
Выражение |
|
(3.4) имеет |
|
смысл, если зна- |
|
менатель отличен |
|
от нуля. Посколь- |
|
ку при вращении |
|
0, теорема |
Рис. 3.7. |
доказана. |
134

Эта теорема не только доказывает существование мгновенного центра скоростей, но указывает, как его найти: надо
вектор скорости vA повернуть на 90° в сторону вращения фи-
гуры и отложить отрезок AP |
vA / . |
|
|
|
|
Пусть мгновенный центр скоростей P является полюсом. |
|||||
|
|
|
|
|
|
Тогда в (3.2) вместо vA будет |
vP = 0 и |
vB |
= vBP , где |
vBP |
BP и |
vBP BP . В произвольный момент времени, когда |
0, |
||||
скорости точек плоской фигуры распределяются так же, как при вращении ее вокруг мгновенного центра скоростей. Поэтому мгновенный центр скоростей часто условно называют мгновенным центром вращения.
Применяя (3.4) для точек А и В, получаем vA |
AP |
и |
||||
vB BP . Отсюда |
|
|
|
|
|
|
|
vA |
|
AP |
|
|
|
|
|
|
|
. |
(3.5) |
|
|
vB |
BP |
|
|||
Скорости точек плоской фигуры прямо пропорциональны их расстояниям от мгновенного центра скоростей. На рис. 3.7, а - в в соответствии с (3.5) и изложенным выше даны примеры определения полюса P по двум заданным векторам скоростей двух точек тела для частных случаев.
135

Следующие две теоремы относятся к случаям, когда = 0, и мгновенный центр скоростей не существует.
Теорема 3.2. Если скорости vA и vB двух точек плоской фигуры, движущейся в своей плоскости, в данный момент па-
Рис. 3.8.
раллельны и не перпендикулярны прямой, соединяющей точки A и B, то скорости всех точек плоской фигуры в данный момент равны между собой, и угловая скорость фигуры равна нулю, т. е. мгновенный центр скоростей P не существует (рис. 3.8, а - в).
Доказательство. В соответствии с (3.3) vA cos |
|
vB cos . |
|||||||
|
|
|
|
|
|
|
|
|
|
Если |
90°, то cos |
0. Тогда vA |
vB . Так как vA |
vB , то |
|||||
|
|
|
|
|
|
|
|
|
|
vA |
vB . Тогда из (3.2) |
vBA |
0 |
, AB |
= 0 и |
|
= 0. Но если = |
||
|
|
|
|
|
|
|
|
|
|
0, то для любой точки фигуры имеем vM |
vA |
vMA |
и, так как |
||||||
|
|
|
|
|
|
|
|
|
|
= 0, то vMA AM |
0 и |
vM |
vA . |
|
|
|
|
|
|
Теорема 3.3. Если векторы скоростей двух какихлибо точек плоской фигуры, движущейся в своей плоскости, равны между собой, то скорости всех точек плоской фигуры в данный момент времени также равны и угловая скорость фигуры равна нулю. Доказательство этой теоремы совпадает со второй частью доказательства предыдущей теоремы.
С течением времени мгновенный центр скоростей меняет свое положение относительно плоской фигуры S. Движение фигуры S можно представить как бесконечную последовательность бесконечно малых поворотов вокруг постоянно меняющихся мгновенных центров скоростей.
§ 3.3. Ускорения точек тела в плоскопараллельном
136
|
|
|
|
|
|
|
|
|
движении |
|
|||||||
|
|
Дифференцируя |
первое |
выраже- |
|||||||||||||
ние (3.2) по времени, получаем уско- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рение |
точки |
В |
|
aB |
|
aA |
aBA , где |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv |
A |
|
d 2 r |
|
|
|
|
|
|
|
|
|
|
|
|
a A = |
|
|
A |
|
|
|
- ускорение точки А |
||||||||||
|
dt |
dt2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
относительно |
неподвижной |
системы |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(рис. 3.4); |
= |
|
dv |
BA |
|
|
d 2r |
- ускоре- |
|||||||||
aBA |
|
|
|
|
|
|
|||||||||||
|
|
dt |
|
dt2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ние точки В относительно подвижной системы (рис. 3.4). |
|||||||||||||||||
Поскольку ускорение |
|
|
|
точки В при ее вращении вме- |
|||||||||||||
aBA |
|||||||||||||||||
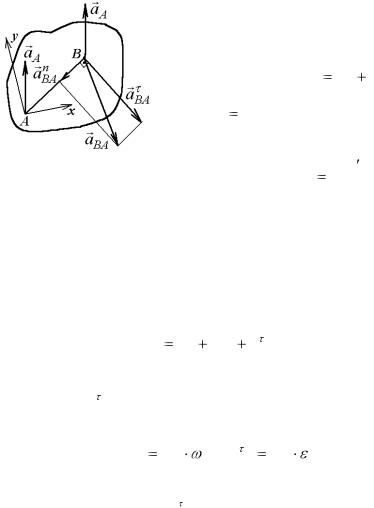
Рис. 3.9. |
сте с плоской фигурой S вокруг точки |
|
А можно разложить на нормальное и |
||
|
касательное ускорения (см. рис. 3.9 и формулы (2.10) и (2.11)), получаем
|
|
n |
|
|
aB |
aA |
aBA |
aBA . |
(3.6) |
n |
|
|
|
|
Ускорение aBA направлено из точки В в точку А (рис. 3.9), |
||||
|
|
|
|
|
а ускорение aBA |
перпендикулярно отрезку АВ. Эти ускорения |
|||
определяются по формулам |
|
|
||
|
aBAn |
AB |
2 , |
aBA AB . |
|
|
|
|
|
Чтобы получить вектор aB |
ускорения точки В, надо сло- |
|||
|
n |
|
(рис. 3.9). |
|
жить векторы aA |
, aBA |
и aBA |
||
Итак, ускорение любой точки тела, совершающего плоское движение, можно представить в виде векторной суммы вектора ускорения полюса и вектора ускорение этой же точки относительно полюса, которое в свою очередь можно представить в виде суммы векторов нормального и касательного ускорений точки относительно полюса.
137
