
Учебное пособие 1828
.pdf
Для этого сообщают мысленно всем звеньям передачи вращение с угловой скоростью - H , то есть равной по моду-
лю и противоположной по направлению угловой скорости водила H . Тогда, на основании результатов § 6.1, водило в этом сложном движении станет неподвижным, а любое зубчатое колесо радиуса rk приобретет относительно водила абсолют-
ную угловую скорость
( H ) |
|
H , |
k |
k |
где k - абсолютная угловая скорость колеса k относительно стойки.
Здесь символ |
( H ) |
обозначает угловую скорость звена с номе- |
|
k |
|
ром k относительно неподвижного водила H .
В суммарном (сложном) движении водило Н останавливается, и планетарная зубчатая передача превращается в рядовую зубчатую передачу, в которой все зубчатые колеса дви-
жутся относительно водила со скоростями |
( H ) |
. При этом оси |
|
k |
|||
|
|
всех колес передачи станут неподвижными и зависимости ме-
жду угловыми скоростями ( H ) можно будет определить, ис-
k
пользуя ранее полученные формулы для рядовых зубчатых передач.
Кинематику планетарных и дифференциальных передач можно рассчитывать и с помощью мгновенных центров скоростей (§ 3.2) или планов скоростей.
§ 6.4. Примеры решения задач
Задача 6.1. В планетарном механизме (рис. 6.11) зубчатое колесо 1 радиуса r1 неподвижно, а водило H вращается относительно центральной оси с угловой скоростью H . Опреде-
198

лить угловую скорость зубчатого колеса 2. Решение. Пусть 1 и 2
абсолютные угловые скорости зубчатых колес 1 и 2, то есть скорости этих колес относительно системы координат Ax1 y1 . Сообщив всем звеньям передачи угловую скорость  H , полу-
H , полу-
чим в обращенном движении следующие угловые скорости
Рис. 6.11. |
|
|
|
( H ) |
0 |
H , |
( H ) |
|
, |
||||||
|
|
|
1 |
2 |
|
2 H |
|||||||||
|
|
|
|
|
|
|
|
( H ) |
|
|
|
|
|
0 . |
|
|
|
|
|
|
|
|
1 |
H |
|
H |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
В передаче имеется одно внешнее зацепле- |
|||||||||||||||
ние и поэтому |
k |
1 . Тогда по формуле (6.8) |
|
||||||||||||
для угловых скоростей относительно системы |
|
||||||||||||||
координат, связанной с ставшим неподвижным |
|
||||||||||||||
водилом, получаем соотношение |
|
|
|
|
|
||||||||||
|
( H ) |
|
r2 |
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
1 |
|
|
, или |
|
|
H |
|
|
. |
|
|
|||
|
( H ) |
|
|
|
|
|
|
|
|
|
|||||
|
|
r1 |
|
|
|
|
|
|
r1 |
|
|
||||
2 |
|
|
|
2 |
H |
|
|
|
|||||||
Отсюда находим абсолютную угловую ско- |
|
||||||||||||||
рость колеса 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
H ( 1 r1 / r2 ). |
|
|
|
|
|
||||
Поскольку |
r1 |
0 и |
r2 |
0 , направления угло- |
|||||||||||
вых скоростей |
|
и |
|
всегда совпадают. |
|
||||||||||
|
|
|
2 |
|
|
H |
|
|
|
|
|
|
|
|
|
Решение методом планов скоростей. Ско- |
|
||||||||||||||
рость точки В водила относительно системы |
|
||||||||||||||
Ax1 y1 будет равна vB |
H rAB . Скорость точки К |
||||||||||||||
колес 1 и 2 равна нулю, поскольку эта точка колеса 1 неподвижна, и для колеса 2 является мгновенным центром скоростей. Точка В колеса 2 имеет скорость vB относительно системы
199

Ax1 y1 , поэтому абсолютная угловая скорость
колеса 2 относительно системы |
Ax1 y1 будет |
|
равна |
|
|
2 vB / r2 |
H ( r1 r2 ) / r2 |
H ( 1 r1 / r2 ) . |
Задача 6.2. Определить соотношение между угловыми скоростями зубчатых колес в планетарной дифференциальной передаче, схема которой изображена на рис. 6.10.
Решение. Пусть H , k и m абсолютные угловые скорости водила и центральных зубчатых колес k и m , а l и l абсолютные угло-
вые скорости сателлитов. Эти скорости определены относительно системы координат связанной со стойкой. Тогда по определению передаточного отношения для планетарной дифференциальной передачи имеем
i |
|
k |
. |
|
|
||
|
km |
||
|
|
m |
|
В этом выражении обе угловые скорости могут быть неизвестными.
Сообщив всем звеньям передачи угловую скорость  H , получим в обращенном движении следующие угловые скорости
H , получим в обращенном движении следующие угловые скорости
( H ) |
|
H , |
( H ) |
|
H , |
k |
k |
m |
m |
||
( H ) |
|
H , |
( H ) |
|
H 0 . |
l |
l |
H |
H |
В передаче имеется одно внешнее зацепление и поэтому k 1 . Тогда по формуле (6.8) для угловых скоростей относительно системы координат, связанной с, ставшим неподвижным, водилом, получаем соотношение
i( H ) |
( H ) |
|
( H ) |
|
( H ) |
|
rl rm |
|
zl zm . |
|||||
k |
|
k |
|
l |
|
|
||||||||
km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( H ) |
|
( H ) |
|
( H ) |
|
rk rl |
|
zk zl |
||||||
|
m |
|
l |
|
m |
|
|
|||||||
200

Поскольку угловые скорости сателлитов одинаковы
величины
Тогда
|
( H ) |
H и |
( H ) |
|
H сокращаются. |
|
l |
l |
l |
l |
|||
|
|
|
k |
H |
i( H ) . |
(6.11) |
|
|
|
|
|
||
|
|
|
|
|
km |
|
|
|
|
m |
H |
|
|
Правая часть этого выражения известна, поскольку радиусы или числа зубьев колес всегда предполагаются известными. Это соотношение содержит три неизвестных величины - k , m и H . Задавая какие – либо две из
этих величин, из этого соотношения можно определить третью величину. Составление выражения (6.11) равносильно решению задачи кинематики планетарной дифференциальной передачи.
|
|
Задача |
6.3. |
В |
||
|
планетарной |
диф- |
||||
|
ференциальной |
пе- |
||||
|
редаче, схема кото- |
|||||
|
рой |
изображена |
на |
|||
|
рис. 6.10, колесо m |
|||||
|
закреплено на стой- |
|||||
|
ке |
и |
неподвижно. |
|||
Рис. 6.12. |
Определить |
переда- |
||||
точное |
отношение |
|||||
|
||||||
от колеса k к водилу H в получившейся при этом обыкновенной планетарной передаче, схема которой изображена на рис. 6.12.
Решение. Для обыкновенной планетарной передачи соотношение (6.11) содержит только две неизвестных величины - k и H , поскольку колесо m закреплено и
m = 0. Тогда выражения (6.11) принимает вид
201

|
|
|
k |
H |
1 |
k |
i( H ) . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
km |
|
|
|
|
H |
|
H |
|
Величина |
k |
|
определяет отношение угловых скоро- |
||||
H |
|
||||||
|
|
|
|
|
|
|
|
стей зубчатого колеса k |
и водила H в обыкновенной пла- |
||||||
нетарной передаче. Учитывая, что эта передача получена
при |
закреплении колеса |
m , используют |
обозначение |
ikH( m ) |
k / H . Тогда получаем соотношение |
|
|
|
i( m ) |
1 i( H ) . |
(6.12) |
|
kH |
km |
|
Последняя формула называется формулой Виллиса.
§ 6.5. Сложение вращений тела вокруг пересекающихся осей
Пусть относительным движением тела 1 (рис. 6.13) является вращение с угловой скоростью 1 , вокруг оси a1a , укреп-
ленной на кривошипе 2, а переносным является вращение кривошипа с угловой скоростью 2
вокруг оси b1b , которая с осью
a1a пересекается в точке О.
Схема сложения вращений в таком случае движения тела вокруг пересекающихся осей показана на рис. 6.13.
Очевидно, что в этом случае скорость точки О, как лежащей одновременно на обеих осях, будет равна нулю. Следовательно, результирующее движение тела является движением вокруг неподвижной точки О и для каждого элементарного промежутка времени является элементарным
202

поворотом с угловой скоростью вокруг мгновенной оси, проходящей через точку О (§
4.1).
Чтобы определить вектор , определим скорость какой-либо точки М тела, вектор -
радиус которой OM r . В относительном движении вокруг оси Oa точка М, согласно (§ 5.2)
r |
|
|
|
получает скорость v |
|
1 |
r ; в переносном же |
|
|
|
движении вокруг оси Ob точка получает ско-
e |
|
|
|
|
|
|
|
|
|
рость v |
|
2 |
r . Следовательно, абсолютная |
||||||
|
|
|
|
|
|
|
|
|
|
скорость точки М равна |
|
|
|
|
|||||
|
|
|
|
e |
r |
|
|
|
|
|
|
|
v |
v |
v |
( |
2 |
1 ) |
r . |
Так как результирующее движение тела является мгновенным вращением с некоторой угловой скоростью , то должно быть
|
|
|
v |
|
r . |
Такие результаты будут получаться для всех точек тела (т.е. при любых r ). Отсюда заключаем, что последние два равенства будут выполняться всегда, если
 1
1  2 . (6.13)
2 . (6.13)
Следовательно, при сложении вращений вокруг двух осей, пересекающихся в точке О, результирующее движение тела будет мгновенным вращением вокруг оси Ос, проходящей через точку О. Вектор угловой скорости этого вращения равен векторной сумме относительной и переносной угловых скоростей. Мгновенная ось вращения Ос направлена вдоль вектора , т. е. по диагонали параллелограмма, построен-
203
ного на векторах 1 и 2 .
С течением времени ось Ос меняет свое положение и в пространстве и относительно тела, описывая коническую поверхность, вершина которой находится в точке О.
Если тело участвует одновременно в n независимых вращениях вокруг n осей, пересекающихся в точке О, то, последовательно применяя равенство (6.13), получим, что результирующее движение является мгновенным вращением вокруг оси, проходящей через точку О, а угловая скорость этого движения
 1
1  2
2  n . (6.14)
n . (6.14)
§ 6.6. Кинематические уравнения Эйлера
Пользуясь результатами предыдущего параграфа, найдем угловую скорость тела, движущегося вокруг неподвижной точки О, если это движение задано уравнения-
ми (4.1).
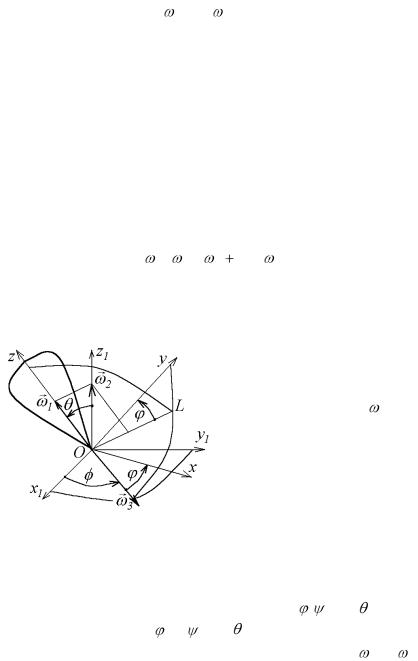
Построим оси неподвижной Ox1 y1 z1 системы координат K1 и оси Oxyz системы K , жестко связанной с те-
лом и движущейся вместе |
с ним (рис. 6.14), и |
|||||
покажем на чертеже углы |
Эйлера , и |
|
. При |
|||
изменении углов , |
и |
тело будет вра- |
|
|
||
щаться вокруг осей |
Oz, Oz1 и OK. Пусть |
|
1 , |
|
2 , |
|
204

3 - векторы угловых скоростей этих вращений,
направленные вдоль соответствующих осей. Модули этих угловых скоростей
|
d |
, |
|
d |
, |
|
d |
. |
|
1 |
|
2 |
|
3 |
|
||||
dt |
dt |
dt |
|||||||
|
|
|
|||||||
|
|
|
|
|
|
(6.15)
Тогда по формуле (6.13) угловая скорость тела в данный момент времени будет равна
 1
1  2
2  3 . (6.16)
3 . (6.16)
Для определения вектора , найдем его проекции на подвижные оси системы K . Из равенства (6.16) имеем:
x  1x
1x  2 x
2 x 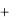 3 x y
3 x y  1 y
1 y  2 y
2 y  3 y
3 y
z  1z
1z  2 z
2 z  3 z
3 z
(6.17)
Проекции векторов 1 и 3 определяются
непосредственно по рис. 6.14 с учетом обозна-
чений (6.15)
1x 1y |
0 , |
1z |
, |
|
|
|
3x |
cos , |
sin |
, |
|
3 z |
0 . |
|
|
3 y |
|
|
|
||
Для определения проекций |
|
2 |
проведем че- |
||||
|
|
|
|
|
|
|
|
рез оси |
Oz1 |
и Oz плоскость, пересекающуюся с |
|||||
плоскостью Оху вдоль линии OL. Так как линия |
|||||||
ОК перпендикулярна к плоскости |
|
zOz1 , то она |
|||||
перпендикулярна и к линии OL ( |
|
KOL 90 , а |
|||||
LOy |
). Тогда, определяя составляющую век- |
||||||
205

тора |
|
на линию OL, а затем ее проекции на |
||
|
2 |
|
|
|
оси Ох и Оу, получим |
|
|
||
|
|
2 x |
sin sin |
, |
|
|
|
|
|
2 y
2 z
 sin cos ,
sin cos , 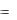 cos .
cos .
Подставляя все определенные проекции в правые части равенств
(6.17), получим
x |
sin |
|
sin |
cos |
, |
|
|
|
|
|
|
y |
sin |
|
cos |
sin |
, |
|
|
|
|
|
|
|
z |
|
cos . |
|
|
|
|
|
|
|
|
(6.18)
Соотношения (6.18) называются кинематическими уравнениями Эйлера. Они определяют проекции вектора угловой скорости тела на подвижные оси системы Oxyz , связанные с телом, через углы Эйлера. Для использования равенств (6.18) необходимо иметь только уравнения движения тела (4.1), выражающие зависимости углов Эйлера от времени и определить по ним соответствующие производные.
§ 6.7. Сложение поступательного и вращательного
движений. Винтовое движение
Рассмотрим сложное движение твердого тела, состоящее из поступательного и вращательного движений. Соответствующий пример показан на рис. 6.15. Здесь относительным движением
Рис. 6.15. тела является вращение с
206

угловой скоростью вокруг оси Аа, укрепленной на платформе 2, а переноснымпоступа-
тельное движение платформы со скоростью v . Одновременно в двух таких движениях уча-
ствует и колесо 3, для которого относительным движением является вращение вокруг его оси, а переносным - движение той же платформы. В зависимости от значения угла α между векторами
иv (для колеса этот угол равен 90°) возможны три случая.
6.7.1.Скорость поступательного движения
перпендикулярна к оси вращения ( v  ) Пусть сложное движение тела состоит из
) Пусть сложное движение тела состоит из
вращательного движения вокруг оси Аа с угловой скоростью и поступательного движения со скоростью v , перпендикулярной к (рис. 6.16). Легко видеть, что это движение является относительно любой плоскости, перпендикулярной к оси Аа, плоскопараллельным движением, подробно изученным в главе 3. Если считать точку А полюсом, то рассматриваемое движение, как и всякое плоскопараллельное движение, будет действительно состоять из поступа-
тельного движения со скоростью v , т. е. со скоростью полюса, и из вращательного вокруг оси Аа, проходящей через полюс.
|
|
|
|
|
|
|
|
|
Вектор |
v |
можно заменить парой угловых |
|
|||||
скоростей |
|
и |
(§ |
6.2), взяв = |
, a |
|||
= - . При этом расстояние АР найдется из |
|
|||||||
равенства |
v |
= |
AP. Учитывая, что |
= |
, |
|||
получаем |
|
|
|
|
|
|
|
|
|
|
|
AP |
|
v |
. |
|
|
|
|
|
|
|
|
|
||
207
