
- •Введение
- •Рис. 2.18. График государственного регулирования рынка
- •Совокупная прибыль
- •Рис. 2.24. Диверсификация цен по времени
- •3.5. Двойственная задача потребительского выбора
- •3.6. Функция спроса Маршалла
- •3.7. Модель общего равновесия Вальраса
- •3.8. Рыночное равновесие в модели Леонтьева
- •Таблица 3.2
- •Значения коэффициентов парной корреляции
- •Таблица 4.1
- •Исходные данные для предельного анализа
- •Рис. 4.1. Результаты регрессионного анализа зависимости между ценой продукта и его количеством
- •Таблица 4.3
- •Исходные данные для решения задачи оптимизации
- •Рис. 4.4. Исходные данные для расчета
- •Рис. 4.6. Результаты расчета
- •Таблица 4.5
- •Таблица 4.6
- •Исходные данные по изделиям
- •Таблица 4.10
- •Таблица 4.11
- •Оптимальное значение целевой функции – 240,000.
- •Общий вид матрицы игры
- •Таблица 5.2
- •Матрица игры
- •Таблица 5.4
- •Таблица 5.5
- •Матрица выигрышей
- •Рассмотрим игру, платежная матрица которой имеет размерность
- •Исходные данные для расчета
- •Оценка рентабельности
- •Показатели рентабельности характеризуют финансовые результаты и эффективность деятельности предприятия. Они измеряют доходность предприятия.
- •Рекомендуемые значения оцениваемых показателей
- •Анализ рентабельности
- •Анализ деловой активности
- •Анализ финансовой устойчивости
- •Вопросы и задания
- •Заключение
- •Библиографический список
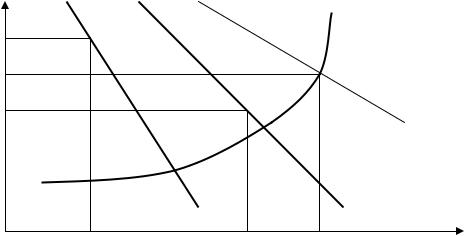
Р1 |
|
MC |
|
|
|
Р2 |
|
MRT |
|
|
|
MR1 |
|
MR2 |
Q1 |
Q2 |
QT |
Рис. 2.23. Диверсификация цен по категориям товаров |
||
Совокупная прибыль
П = P1 ×Q1 + P2 ×Q2 − C(QТ ). |
(2.17) |
QT = Q1 + Q2. |
(2.18) |
Фирма будет увеличивать объем и сбыт товаров обоих сортов Q1 и Q2 до тех пор, пока дополнительная прибыль от реализации последней единицы
продукции не станет равна нулю. |
|
|
|
|
Для продукции первого сорта имеем |
|
|
|
|
П = |
(P1 ×Q1 ) − |
C |
= 0, |
(2.19) |
|
||||
Q |
Q1 |
Q1 |
|
|
где (P1 ×Q1 ) / Q1 = MR1 − дополнительный доход от сбыта дополни-
тельной единицы продукции первого сорта;
С/ Q1 = MC −издержки производства дополнительной единицы
продукции.
Таким образом,
MR1=MC. |
(2.20) |
По аналогии для второго сорта продукции MR1 = МС.
Таким образом, цены и объем производства должны быть такими, что-
бы выполнялись соотношения |
|
MR1 = MR2 = МС, |
(2.21) |
т.е. предельный доход должен быть равным для обоих сортов и равным |
|
предельным издержкам. |
|
Выразим предельный доход через эластичность спроса: |
|
MR = P (l+1/Ed). |
(2.22) |
Тогда MR1 = P1(1+1/E1), MR2 = P2(1+1/E2),
27
где E1 и Е2 - эластичности спроса на продукцию первого и второго сорта. Приравнивая MR1 и MR2, получим соотношение для диверсификации цен:
P1 |
= |
(1 +1/ E2 ) . |
(2.23) |
||
|
|||||
P (1 |
+1/ E |
) |
|
||
2 |
|
|
1 |
|
|
Очевидно, что более высокая цена будет назначена на ту продукцию, спрос на которую менее эластичен. Например, если эластичный спрос на продукцию первого сорта равен -2, а на продукцию второго сорта равен -4, то
P1/Р2 = (1-1/4)/(1-1/2) = (3/4)/(1/2) =1,5.
Таким образом, цена на товар первого сорта должна быть в 1,5 раза выше, чем на товар второго сорта.
Совокупный объем производства Q1+Q2=QT определяется путем почленного сложения кривых MR1 и MR2, что дает кривую MRT, ее пересечение с кривой МС определяет совокупный объем производства QT.
2.9.4. Диверсификация цен по времени
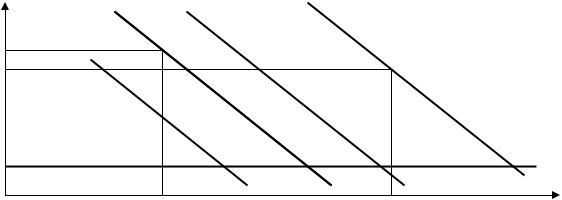
Диверсификация цен по времени устанавливается, как правило, на новые виды товаров, при этом определяются кривые спроса для небольшой группы потребителей, высоко оценивающих этот товар (например, видеотехнику или компьютеры) и готовых приобрести его по высокой цене, и кривая D2 для более широкой группы потребителей, готовых воздержатся от покупки, если цена слишком высока. Стратегия заключается том, чтобы предложить товар сначала по цене P1 потребителям первой группы, а затем по цене Р2 - потребителям второй группы (рис.2.24).
D2 |
|
|
|
P1 |
|
|
|
P2 |
|
|
|
|
|
|
MC |
MR1 |
D1 |
MR2 |
|
Q2 |
|
Q1 |
Q |
Рис. 2.24. Диверсификация цен по времени |
|
||
Ценообразование при максимальном спросе представляет собой форму диверсификации цен по времени. Для некоторых товаров и услуг спрос дос-
28
тигает максимума в определенные периоды времени (для дорог - в часы пик, для электричества - вечером, для мест отдыха - в выходные дни).
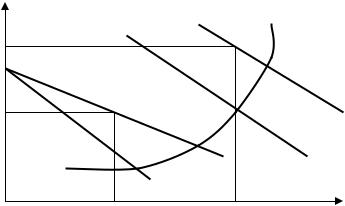
При этом и предельные издержки в это время также возрастают из-за ограничения мощностей. Таким образом, цены будут выше во время пиковых периодов (рис. 2.25).
Р1 |
|
MC |
|
|
|
Р2 |
|
D1 |
|
MR1 |
|
|
|
|
|
D2 |
|
|
MR2 |
|
Q2 |
Q1 |
Q |
Рис. 2.25. Диверсификация цен по времени |
||
На рис.2.25 D1 - кривая спроса для пикового периода, D2 - для остального времени. Фирма устанавливает предельный доход, равный предельным издержкам в каждый период, получая высокую цену Р1 в пиковый период и низкую Р2 в остальное время с соответствующими объемами производства
Q1 и Q2.
Вопросы и задания
1.Что показывают графики кривых спроса и предложения?
2.Определите графически точку рыночного равновесия.
3.Начертите график спроса и предложения. Определите, как изменится график при росте цены на товар.
4.Приведите примеры товаров, для которых существует несколько точек рыночного равновесия.
3.ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ
3.1. Виды производственных функций
Производственные функции в широком смысле охватывают моделирование зависимостей, существующих между такими показателями произ-
29
водственной деятельности, как объем выпускаемой продукции, капитальные затраты, фондоотдача, производительность труда и т.д.
В более узком смысле под производственной функцией понимается зависимость выпуска продукции от затрат различных производственных ресурсов. В общем виде функция может быть записана в виде
P = f (F1,F2 ,F3 Fn ), |
(3.1) |
где P - выпуск продукции;
Fi - факторы, определяющие величину выпуска продукции (затраты
труда, материалов и т.д.). Зависимость между затратами различных видов ресурсов и объемом выпуска продукции должна быть выражена уравнением множественной регрессии.
При разработке ЭММ нередко исходят из предположения о линейной зависимости между затратами ресурсов и выпуском продукции. Однако предположение о линейном характере зависимости затрат и выпуска продукции является значительно упрощенным. Если по отношению к затратам материалов и сырья это предположение может быть принято, то по отношению машин это предположение не всегда может быть принято.
Построение моделей оптимального планирования, приближающихся к реальной экономической действительности, требуют углубления и уточнения связей между затратами ресурсов и выпуском продукции.
Наиболее часто в качестве нелинейной функции используется уравне-
ние
P = a |
o |
×Fa1 |
×Fa2 |
× ×Fan . |
(3.2) |
|
1 |
2 |
n |
|
Этому уравнению соответствует линейно-логарифмическая функция
In P = Inao +a1 ×In F1 + +an ×In Fn . |
(3.3) |
Для каждого фактора можно определить абсолютную скорость, с которой в пределе возрастает выпуск продукции с ростом затрат данного фактора. Эта скорость определяется как частная производная выпуска продукции по затратам данного вида ресурсов:
δP |
= a |
o |
×a |
1 |
×Fa1 |
×Fa2 |
× ×Fan . |
(3.4) |
|
||||||||
δF1 |
|
1 |
2 |
n |
|
|||
|
|
|
|
|
|
|
||
Абсолютная скорость зависит от величины всех компонентов уравнения. Отношения частных производных для двух каких-либо факторов служат своеобразными нормами заменяемости этих ресурсов с точки зрения производства данной продукции.
Наряду с абсолютной скоростью большой интерес представляет изменение выпуска продукции при увеличении затрат ресурсов данного вида на
1%.
Для получения относительной скорости нужно величину абсолютной скорости умножить на отношение затрат ресурсов к выпуску продукции.
Так, для первого фактора относительная скорость составляет
30
δP |
× F1 |
= |
(ao ×a1 ×F1a1 ×F2a2 × ×Fnan )×F1 |
= |
ao ×aa1 ×F1a1 ×F2a2 × ×Fnan |
= a |
1 |
(3.5) |
||||
δF1 |
P |
|
P |
|
a |
o |
×Fa1 |
×Fa2 |
× ×Fan |
|
|
|
|
|
|
|
|
|
1 |
2 |
n |
|
|
|
|
Относительная скорость изменения объема выпуска продукции от изменения затрат на 1 % называется эластичностью выпуска по затратам и обозначается символом Е. Для любого i фактора выполняется условие
E |
i |
= |
δP |
× Fi |
= a |
. |
(3.6) |
|
δF |
||||||||
|
|
P |
i |
|
|
|||
|
|
|
1 |
|
|
|
|
Таким образом, для уравнения типа (3.2) эластичность выпуска продукции для каждого фактора является величиной постоянной и равна соответствующему коэффициенту уравнения регрессии. При любом объеме затрат и выпуска увеличение затрат i-го вида ресурсов на 1 % ведет к увеличению выпуска продукции на ai %.
Будем предполагать, что фирма производит n различных видов продукции. Обозначим через q=(q1, ….. qn)T вектор выпуска, компонентами которого являются выпуски каждого конкретного вида продукции. Предположим, что для осуществления выпуска используется m видов факторов производства. Обозначим через x=(x1, ….. xm)T вектор затрат факторов производства, компонентами которого являются объемы потребления каждого конкретного фактора.
Множество векторов выпуска продукции образуют так называемое
пространство выпуска:
S ={q = (q1 ,...,qn )T |
|
qi ≥ 0,i = |
|
} . |
(3.7) |
|
1,n |
Множество векторов затрат факторов производства образуют так на-
зываемое пространство затрат:
R ={x = (x1 ,..., xm )T |
|
xi ≥ 0,i = |
|
}. |
(3.8) |
|
1,m |
Технологическая связь между затратами факторов производства и объемом выпуска продукции описывается с помощью производственной функции.
Функция q=f(x), которая каждому вектору затрат из пространства затрат ставит в соответствие максимальный выпуск, который может быть произведен при данных затратах, называется производственной функцией фир-
мы.
В общем случае производственную функцию можно записать в неявной форме:
F(x, q, A) = 0,
где A представляет собой технологическую матрицу размерами n x m.
Если в качестве независимых аргументов рассматриваются затраты, то производственную функцию называют функцией выпуска. Если в качестве
31
независимых аргументов рассматриваются объемы выпуска, то производственную функцию называют функцией затрат. В дальнейшем для простоты выкладок мы будем предполагать, что фирма выпускает только один вид продукции.
С понятием производственной функции связано понятие предельного продукта.
Предельным продуктом i-го фактора производства (MPi-marginal product (англ.)) называют дополнительный объем выпуска, который будет произведен при потребления каждой дополнительной единицы данного фактора:
MPi (x) = lim |
f (x1 ,...,xi + ∆x,...,xm ) −u(x1 ,..., xi ,..., xm ) |
= |
∂f (x) . |
(3.9) |
|
∆xi |
|||||
∆x→0 |
|
∂xi |
|
Производственная функция обладает следующими свойствами.
1. C увеличением потребления какого-либо фактора значение выпуска продукции возрастает:
∂f (x) = MPi(x) ≥ 0. |
(3.10) |
∂xi |
|
2. C увеличением объема потребления какого либо фактора скорость выпуска продукции убывает:
∂MPi (x) =≤ 0. |
(3.11) |
∂xi |
|
3. Производственная функция является однородной функцией своих аргументов:
f (t x) = t β f (x), |
(3.12) |
где β представляет собой степень однородности.
Рассмотрим основные виды производственных функций:
1. Неоклассическая производственная функция (производственная функция Кобба-Дугласа):
a |
x |
a |
2 ....x |
|
am |
, |
|
|
f (x) = Ax 1 |
2 |
m |
|
|
|
|||
1 |
|
|
|
|
|
|
||
m |
|
|
|
|
|
|
|
|
A 0, ∑ai =1, |
ai |
≥ 0, i = |
|
(3.13) |
||||
1, m |
||||||||
i=1
Здесь величины a1, ….. am представляют эластичности выпуска к изменению объема соответствующего фактора производства, А- масштабирующий множитель.
2. Производственная функция «затраты-выпуск» (функция Леонтьева):
|
|
xm |
|
|
|
f (x) = min |
x1 |
,..., |
|
(3.14) |
|
|
am |
||||
a1 |
|
. |
|||
Эта функция задает пропорции, в которых осуществляется потребление затрат факторов производства для осуществления выпуска одной едини-
32
цы продукции. Величины a1, ….. am представляют собой пропорции объемов потребления соответствующих факторов производства.
3. Линейная производственная функция:
m |
|
f (x) = a1 x1 + a2 x2 +... + am xm = ∑ai xi . |
(3.15) |
i=1
Данное семейство функций полезности описывает ситуацию, когда факторы производства являются полностью взаимозаменяемыми. Коэффициенты a1,…..am представляют собой пропорции, в которых один фактор может быть заменен другим.
Переменные издержки касаются использования имеющихся в распоряжении фирмы факторов производства и изменяются в соответствии с объемом выпуска продукции.
3.2. Функция Кобба-Дугласа
Одной из первых практических работ в области изучения производственных функций было исследование Ч.Кобба и П.Дугласа по данным обрабатывающих отраслей промышленности США за 1899-1922 гг.
В этих исследованиях была принята функция вида
Y = ao ×X1a1 ×Xa22 , |
(3.16) |
где Y - объем выпуска продукции; X1 - затраты труда; X2 - стоимость производственных фондов.
В результате исследователи пришли к выводу, что а1+а2=1, т.е. имеет место неизменный эффект масштаба производства.
Функция валового внутреннего продукта (ВВП) в зависимости от стоимости основных фондов и числа занятых в народном хозяйстве за 19601994 годы имеет вид:
Y=0.931K0.54 L0.59 , |
(3.17) |
где Y– ВВП, млрд р.; К - стоимость основных производственных фондов, |
|
млрд р.; L - число занятых в народном хозяйстве, млн чел. |
|
По данным экономики США за 1980-1995 годы производственная |
|
функция Кобба-Дугласа имеет вид |
|
Y=2.251K0.4 L0.8. |
(3.18) |
Производственная функция Y= F(K, L) называется неоклассической, если она является гладкой и удовлетворяет следующим условиям, поддаю-
щимся естественной экономической интерпретации: |
|
1) при отсутствии одного из ресурсов производство невозможно: |
|
F(0, L) = F(K, 0) = 0; |
(3.19) |
2) с ростом ресурсов выпуск растет:
33

∂F |
> 0 |
∂F |
> 0 ; |
(3.20) |
|
∂L |
∂K |
||||
|
|
|
3) с увеличением ресурсов скорость роста выпуска замедляется:
∂2F |
< 0 |
∂2F |
< 0 |
(3.21) |
|
2 |
∂K |
2 |
|||
∂L |
|
|
|
|
|
4) при неограниченном увеличении одного из ресурсов выпуск неограниченно растет:
f(+∞, L) = F(K, +∞) = +∞. |
(3.22) |
Мультипликативная ПФ задается выражением
Y = AKa1 La2 , |
(3.23) |
где А — коэффициент нейтрального технического прогресса; а1, a2 - коэффициенты эластичности по труду и фондам.
Если a1>0, a2>0, а1 >a2, имеет место трудосберегающий (интенсивный) рост, в противном случае - фондосберегающий (экстенсивный) рост.
Линией уровня на плоскости К, L, или изоквантой, называется множество тех точек плоскости, для которых F(K, L) =Х0=const. Для мультипликативной ПФ изокванта имеет вид
AKa1 La2 |
= X0 |
= const |
|
(3.24) |
||||
или |
a |
|
X0 |
−a |
|
, |
(3.25) |
|
K 1 |
= |
|
L |
2 |
||||
A |
||||||||
|
|
|
|
|
|
|
||
т.е. является степенной гиперболой, асимптотами которой служат оси координат.
Для разных К, L, лежащих на конкретной изокванте, выпуск равен одному и тому же значению X0, что эквивалентно утверждению о взаимозаменяемости ресурсов.
Поскольку на изокванте F(K, L) = Х0 = const, то
dF = |
∂F |
dK + |
∂F |
dL = 0 . |
(3.26) |
|
|
||||
|
∂K |
∂L |
|
||
В этом соотношении ∂∂KF > 0, ∂∂LF > 0 , поэтому dK и dL имеют разные
знаки: если dL<0, что означает сокращение объема труда, то dK>0, т.е. выбывший в объеме dL труд замещается фондами в объеме dK.
Наряду с количественным увеличением объема ресурсов важнейшим фактором роста производства служит научно-технический прогресс, проявляющийся в совершенствовании техники и технологии, повышении квалификации работающих, улучшении организации производства. Технический прогресс обычно отражают в производственных функциях следующего вида:
Y = a |
o |
×Xa1 |
×Xa |
2 |
×eλt , |
(3.27) |
|
1 |
2 |
|
|
|
34
где λ - константа, отражающая темп технического прогресса; t - временной фактор.
Параметр et представляет собой выражение временной тенденции развития производства, связанной с техническим прогрессом, совершенствованием планирования, управления и организации производства.
С учетом ограниченности и резкого повышения стоимости природных ресурсов целесообразно строить производственную функцию следующего вида:
Y = ao ×X1a1 ×Xa22 ×X3a3 , |
(3.28) |
где X3- стоимость используемых природных ресурсов.
При анализе экономических явлений с применением производственных функций возникает вопрос о целесообразности расширения масштабов производства. В этом случае анализируется величина
m
A = ∑am. (3.29)
i=1
Возможны три случая:
1.Если А=1, то увеличение ресурсов в k раз приводит к увеличению объема производства также в k раз.
2.Если A >1, то можно говорить о положительном эффекте расширения масштабов производства, т.к. увеличение ресурсов в k раз приводит к росту объемов производства более чем в k раз.
3.Если A <1, то имеем отрицательный эффект расширения масштабов производства.
На основе производственных функций могут быть построены модели зависимости спроса от доходов:
Y = ao ×X1a1 , |
(3.30) |
где Y - спрос; X1- величина доходов населения.
Коэффициент эластичности a1 показывает, насколько увеличится спрос при росте доходов на 1%. Коэффициент эластичности может быть и отрицательным (когда с ростом доходов населения может снизиться потребление хлеба, картофеля и т.д.).
3.3. Модель Солоу
Модель Роберта Солоу [5, 6] была построена на неоклассической предпосылке господства совершенной конкуренции на рынках факторов производства, обеспечивающей полную занятость ресурсов. Ученый исходил из того, что необходимым условием является равенство совокупного спроса и совокупного предложения. При этом совокупное предложение в его модели определялось на основании производственной функции Кобба-Дугласа, вы-
35
ражающей отношение функциональной зависимости между объемом производства с одной стороны и используемыми факторами и их взаимной комбинацией — с другой.
Целью модели Солоу является ответ на вопросы: каковы факторы сбалансированного экономического роста, какой темп роста может позволить себе экономика при заданных параметрах экономической системы и как при этом максимизируются доходы населения и объем потребления?
В общем виде объем национального выпуска Y является функцией 3-х факторов производства: труда L, капитала K, земли N:
Y = f (L, K, N).
Фактор земли в модели Солоу был опущен ввиду малой эффективности в экономических системах, характеризующихся высоким технологическим уровнем, и поэтому объем выпуска зависит от трудовых и производственных факторов Y = f (L, K).
В развернутом виде эта формула имеет вид:
Y = ( ∆Y / ∆L) L + (∆Y / ∆K) K, |
(3.31) |
где ∆Y / ∆L – предельный продукт труда MPL, ∆Y / ∆K – предельный продукт капитала MPK.
Это значит, что общий продукт равняется сумме произведений затраченного количества труда и капитала на их предельные продукты, т.е. на прирост продуктов ∆Y от увеличения затрат труда ∆L и затрат капитала ∆K. В упрощенном виде y = Y / L, где y – производительность труда; k = K/ L, где k — капиталовооруженность труда. Тогда производственная функция имеет вид y= f (k), где f (k) = F (k,1).
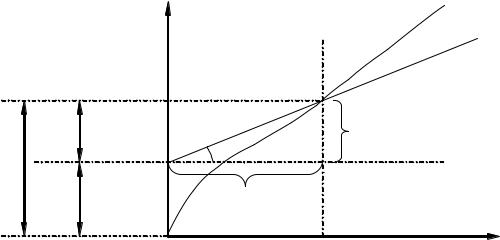
Графическое изображение этой функции имеет вид, показанный на рис. 3.1. Рисунок показывает, что капиталовооруженность k определяет размер выпуска продукции на одного работника: y = f (k).
|
|
h |
|
|
y=Y/L |
f(k) |
|
|
|
||
|
|
М |
|
|
Доля |
МРК |
|
|
капитала |
||
Общий |
tg α |
||
|
выпуск
Доля |
|
1 |
труда |
|
|
|
|
|
|
0 |
K=k/L |
|
|
Рис. 3.1. График производственной функции в модели Солоу
36
При этом tgα = MPK: если k увеличивается на одну единицу, то y возрастает на МРК единиц. По мере роста капиталовооруженности труда его производительность увеличивается, но с убывающей скоростью, т.к. МРК снижается.
Совокупный спрос в модели Солоу определяется инвестиционным и потребительским спросом. Уравнение выпуска продукции на одного работника имеет вид
γ = с + i, |
(3.32) |
где с и i – потребление и инвестиции. |
|
Доход делится между потреблением и сбережениями в соответствии с |
|
нормой сбережения, так что потребление можно представить как |
|
с = (1 — s) y, |
(3.33) |
где s — норма сбережения (накопления). |
|
Тогда у = с + i = (1 — s) y + i, откуда i = sy. В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
В результате условие равенства спроса и предложения может быть представлено как
f (k) = c + i или f (k) = i / s.
Производственная функция определяет предложение на рынке товаров, а накопление капитала – спрос на производственную продукцию. Объем же капитала меняется под воздействием инвестиции выбытия. Инвестиции в расчете на одного работника являются частью дохода, приходящегося на одного работника (i = sy) или
i = s * f(k). |
(3.34) |
Из этого следует, что, чем выше уровень капиталовооруженности k, тем выше уровень производства f(k) и больше инвестиции i.
В модели Р.Солоу норма сбережений – ключевой фактор, определяющий уровень устойчивости капиталовооруженности. Более высокая норма сбережений обеспечивает больший запас капитала и более высокий уровень производства.
Другим фактором непрерывного экономического роста в условиях устойчивой экономики является рост населения. Для устойчивости экономики необходимо, чтобы инвестиции sf(k) компенсировали последствия выбытия капитала и рост капитала (d + n) k, на графике точка Е (рис. 3.2). Однако если рост населения не сопровождается увеличением инвестиций, то это ведет к уменьшению запаса капитала на одного работника.
Таким образом, если страны с более высокими темпами роста населения имеют меньшую капиталовооруженность, то значит – и более низкие доходы.
37
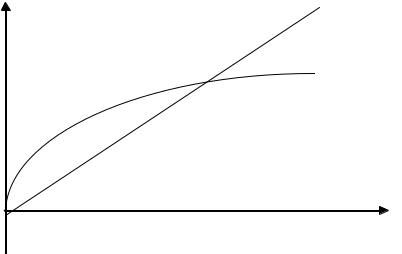
i |
(d+n)k |
E |
k |
0 |
sf(k) |
|
Рис. 3.2. Инвестиции s f(k) и рост капитала (d + n) k
Третьим источником экономического роста после инвестиций и увеличения численности населения является технический прогресс. В неоклассической теории технический прогресс — это качественные изменения в производстве (повышение образования работников, улучшение организации труда, рост масштабов производства) [10].
Включение в модель технического прогресса изменит исходную производственную функцию: Y = f(K, Lε, ε), где ε — эффективность труда одного работника (зависит от здоровья, образования, квалификации), Lε – численность эффективных единиц рабочей силы.
Технический прогресс вызывает прирост эффективности ε с постоянным темпом g. Если g = 5%, то отдача от каждой единицы труда увеличиться на 5 % в год, а это равносильно тому, что объем производства возрастает так, как если бы рабочая сила за год выросла на 5 %. Это трудосберегающая форма технического прогресса.
Если же численность занятых L растет с темпом n, а эффективность ε растет с темпом g, то Lε будет увеличиваться с темпом n + g. Капитал на единицу труда с постоянной эффективностью составит k1 + [K /(Lε)], а объем производства на единицу труда с постоянной эффективностью y1 = Y / (Lε). Состояние устойчивого равновесия достигается при условии
s x f(k1) = (d + n + g) x k1,
где d — норма амортизации.
Из вышеприведенного равенства следует, что существует лишь один уровень капиталовооруженности k1, при которой капитал и выпуск продукции, приходящиеся на единицу труда с неизменной эффективностью, постоянны (рис. 3.3).
38
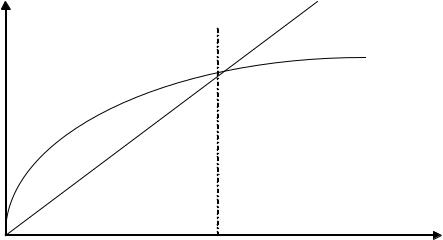
(d+n+g)k1
i
E
Sf(k)
0 |
k 1 |
|
k
Рис. 3.3. Условие постоянства капитала и выпуска продукции, приходящиеся на единицу труда с неизменной эффективностью
В устойчивом состоянии k1 при наличии технического прогресса общий объем капитала К и выпуск Y будет расти с темпом n + g. В расчете на одного работника капиталовооруженность k/L и выпуск Y/L будет расти с темпом g. Таким образом, технический прогресс в модели Солоу — это единственное условие непрерывного экономического развития [10].
3.4. Модель Стоуна
Будем предполагать, что определенное количество единиц каждого вида товара необходимо потребителю в любом случае и вопрос относительно их приобретения не является предметом выбора. Оставшиеся средства потребитель использует для приобретения дополнительных единиц товаров в соответствии со своими предпочтениями.
Обозначим через b1, b2, … bn минимальные количества единиц соответствующих видов товара необходимых потребителю. При этом предполагается, что выполняется условие
n |
|
∑pibi ≤ I. |
(3.35) |
i=1
Также, без умаления общности, будем предполагать, что предпочтения потребителя относительно дополнительных единиц товаров описываются функцией полезности Кобба-Дугласа:
u(x) = (x −b )a1 (x |
2 |
−b )a2 |
....(x |
n |
−b )an , |
||
1 1 |
|
2 |
|
|
n |
||
n |
|
|
|
|
|
|
|
∑ai =1, |
ai ≥ 0, i = |
|
|
|
(3.36) |
||
1, n |
|
||||||
i=1
39
