Методическое пособие 780

K , т.е. скорость звука в однородной упругой среде, которая для воды составляет 1435 м/с, бензина 1116 м/с, масла 1400 м/с.

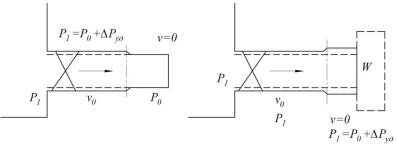
пространения ударной волны в жидкости, которая заполняет упругий трубопровод. Это можно доказать, если рассмотреть элементарное перемещение ударной волны dx за время dt и применить теорему об изменении количества движения. Имеем

P0 Pуд P0 Sdt v0 0 Sdx .

Отсюда a dx Pуд – скорость распространения ударной dt v0

волны. Pуд 0a т.е. получаем формулу аналогичную полученному выражению.

Рис. 3.27. Элементарное перемещение ударной волны

Если скорость в трубопроводе гасится не до 0, а до некоторой конечной величины v , то будет иметь место так называемый неполный гидравлический удар и формула Н. Е. Жуковского принимает вид

151

Эта формула справедлива, когда tзакр t0 24a , т.е. очень быстром закрывании крана, где t0 – фаза гидравлического

удара. При этом происходит так называемая прямой гидравлический удар.

Если tзакр t0 возникает непрямой гидравлический удар, при этом ударная волна возвращается к запорному устройству

висит от a.

Особо следует рассмотреть так называемый тупиковый трубопровод, в котором возможно увеличение ударного давления в два раза.

Действительно, это утверждение можно проиллюстрировать следующим примером, представленном на рис. 3.28.

Рис. 3.28. Тупиковый трубопровод

При мгновенном открытии крана произойдёт увеличение давления в трубопроводе на

152

Возникавшая ударная волна, согласно формуле Н. Е. Жуковского, будет перемещаться со скоростью

В момент подхода к тупику давление во всём объёме жидкости возрастает на величину Pуд и жидкость приобретает ско-

рость v0 , в результате гашения которой, давление ещё возрастает на Pуд v0a. В результате в конце трубопровода возник-

нет новая отражённая волна, за фронтом которой давление возрастёт на 2 Pуд .

Если в конце трубопровода имеется объем V, заполненный жидкостью, например, силовой гидроцилиндр, то этот объем будет оказывать демпферное влияние и давление повышается меньше, чем в 2 раза. При весьма большом объеме V отражение волны практически не происходит.

Полученная формула для

допущения при её выводе, достаточно хорошо подтверждается экспериментом, это можно объяснить тем, что в случае внезапного торможения происходит интенсивный сдвиг слоёв жидкости и, как следствие, большая потеря энергии на внутреннее трение, которая и компенсирует избыток кинетической энергии за счёт неравномерности поля скоростей. Потеря энергии на трение и рассеивание энергии в процессе удара способствует затуханию колебаний.

Для борьбы с гидравлическим ударом предусмотрены следующие способы:

-увеличение времени срабатывания кранов для избежания прямого удара;

-установка компенсаторов в виде местных объёмов или гидроаккумуляторов;

-уменьшение скорости (увеличение d ) и уменьшение длины трубопровода.

153

4. ДВИЖЕНИЕ ГАЗА БЕЗ СКАЧКОВ УПЛОТНЕНИЯ

Соотношения термодинамики. При больших скоростях течения газа, сравнимых со скоростью звука, изменение скорости приводит к изменению плотности. Особенности такого движения изучаются газовой динамикой.

Как известно из курса технической термодинамики, основные параметры состояния газа – давление p , плотность и аб-

солютная температура T связаны для идеальных газов уравнением состояния

где R – газовая постоянная, Дж/(кг∙К). Для воздуха

R287,1 Дж/(кг∙К).

Вбольшинстве задач, рассматриваемых газодинамикой, процессы изменения состояния газа можно считать адиабатными; из-за их быстротечности они осуществляются без теплообмена с окружающими телами. При адиабатном процессе давление и плотность связаны соотношением

постоянном давлении и постоянном объеме.

Для воздуха и других двухатомных газов k 1,4 , для перегретого водяного пара k 1,33 .

Используя уравнение состояния, получим для адиабатного процесса формулы связи между давлением, плотностью и температурой

154

В задаче о движении газа в длинной трубе без теплоизоляции стенок процесс изменения состояния принимается изотермическим: длительный контакт со стенками трубы приводит к тому, что температура газа не отличается от температуры стенки. Для изотермического процесса

p const .

4.1.Скорость звука. Число Маха

Впункте 3.7.6 получены общие формулы для скорости распространения малых возмущений в жидкости, а именно

Процесс изменения параметров газа в звуковой волне, которая представляет собой распространяющиеся в газе слабые возмущения давления и плотности, следует считать адиабатным. Из уравнения (4.2) имеем

Подставляя последнее равенство в формулу для скорости звука, получаем

a k p .

Используя уравнение состояния (4.1), введем в формулу для a температуру T

a kRT .

155

В частности, для воздуха, подставляя величины k и R , имеем

Скорость звука – одна из важнейших механических характеристик газа. Законы его движения резко отличаются в зависимости от соотношения скорости газа v и скорости звука a .

называются дозвуковыми. Если v a и M 1 , течение сверхзву-

ковое.

4.2. Уравнение энергии

Рассмотрим установившееся одномерное движение газа. Если единственной внешней силой, действующей на газ, является сила тяжести, то такое течение описывается дифференциальным уравнением (2.14). Вследствие малой плотности газа допустимо пренебречь в этом уравнении членом, учитывающим изменение высоты струйки над плоскостью сравнения, так как для частицы газа сила веса пренебрежимо мала по сравнению с силами инерции и давления.

Уравнение (2.14) приобретает вид

Выражение (4.5) представляет собой уравнение энергии для газа, записанное в дифференциальной форме.

156

Считая течение адиабатным, выразим в последнем уравнении дифференциал давления через изменение плотности с помощью уравнения адиабаты (4.2)

dp kC k 1d ; dp kC k 2d .

Подставляя уравнение в (4.5) и интегрируя вдоль струйки, получим уравнение энергии в интегральной форме, или уравнение Бернулли-Сен-Венана (1839)

Сравнивая выражение (4.7) с уравнения Бернулли для идеальной несжимаемой жидкости (2.16), видим, что отличие со-

явление этого множителя, который для воздуха, например, ра-

энергию газа входит ещё и его внутренняя энергия. Иногда говорят, что в случае газа к пьезометрическому напору добавляется «температурный напор».

157

Последнее равенство показывает, что при отсутствии теплообмена с внешней средой увеличение скорости вдоль струйки приводит к падению температуры газа и наоборот.

Используя формулу для скорости звука (4.5), уравнение энергии (4.6) можно представить в виде

откуда ясно, что скорость движения газа и скорость звука взаимосвязаны: увеличение скорости течения приводит к уменьшению скорости звука. Вследствие адиабатного охлаждения она меньше скорости звука, соответствующей начальному состоянию газа, когда скорость равна нулю и температура наибольшая.

Выражение (4.9) позволяет выяснить смысл постоянной в правой части уравнения энергии. Действительно, в покоящемся газе v 0 и скорость звука достигает здесь своей наибольшей

Наконец, если использовать понятие энтальпии, или теплосодержания, газа i , рассматриваемое в термодинамике

то уравнение энергии (4.8) приобретает вид

Таким образом, потенциальная энергия газа выражается в различных формах уравнения энергии (4.6)-(4.11) с помощью различных взаимосвязанных параметров – давления, темпера-

158

туры, скорости звука, энтальпии. Ниже показаны примеры применения уравнения энергии в различных формах записи для решения задач одномерного течения.

4.3. Связь скорости газа с сечением потока. Сопло Лаваля

Выясним зависимость скорости течения от площади поперечного сечения потока. Для газа уравнение неразрывности (2.7), или уравнение постоянства массового расхода при установившемся течении имеет вид

имеем

159

при изменении сечения dF происходит по-разному для дозвукового и сверхзвукового течения. В дозвуковом потоке ( v a , M 1, рис. 4.1, а) знаки dv и dF в (4.15) противоположны: уменьшение сечения в конфузорном канале приводит к возрастанию скорости, а в диффузорном канале скорость по потоку уменьшается. При сверхзвуковом течении ( v a , M 1 , рис. 4.1, б) в конфузорном канале поток замедляется, в диффузорном

– ускоряется.

Рис. 4.1. Изменение скорости при разных числах Маха

Чтобы пояснить полученные результаты, которые для сверхзвукового течения кажутся неожиданными, сопоставим уравнения (4.15) и (4.14). Имеем

v

Поскольку левая часть равенства (4.16) всегда положительна, ясно, что знаки d и dv всегда противоположны: рост скорости приводит к уменьшению плотности. Но при дозвуковом течении ( M 2 1 ) скорость изменяется более быстро, чем плотность

160