Методическое пособие 370

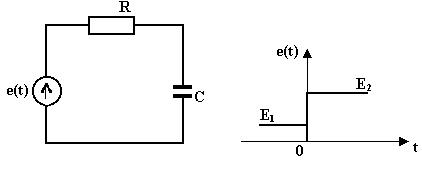
4. Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений.

Это может производиться любым из известных методов.

5. Определение оригиналов искомых токов и напряже-

ний. Производится путем применения таблиц обратного преобразования или формул перехода от изображения к оригиналу.

Пример 1.3. Для схемы, изображенной на рис. 1.20, определить ток в цепи, используя операторный метод, если

Рис. 1.20. RC цепь с графиком входного воздействия

Представленная цепь аналогична той, которая рассматривалась в примере 1.1, где применялся классический метод. Теперь требуется определить ток в цепи, используя операторный метод. Для этого будем применять рассмотренные ранее основные этапы анализа. С учетом их особенностей последовательность решения задачи будет следующей:

1. Осуществляем анализ цепи до коммутации и определяем независимые начальные условия, т.е.

UC 0 UC 0 E1;

40

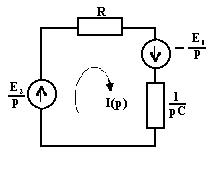
2. Составляем операторную эквивалентную схему цепи после коммутации (рис. 1.21);

Рис. 1.21. Эквивалентная операторная схема по рис. 1.20

3. Записываем уравнение электрического равновесия цепи в операторной форме, используя второй закон Кирхгофа,

41

стью совпадает с результатом из (1.9), при RC.

1.5. Временной метод анализа переходных процессов

Классический и операторный методы применяются, как правило, когда входное воздействие имеет простую структуру в виде прямоугольного отклонения напряжения или тока. В случае, когда на цепь подается электрическое колебание сложной формы, то эти методы становятся малопригодными для анализа переходных процессов и необходимо использовать другие подходы, например, метод суперпозиции (наложения). Так, если воздействие сложной формы представить в виде суммы элементарных сигналов и найти отклик на выходе цепи от каждого из них, то результатом анализа станет простое суммирование таких откликов. Такой подход можно использовать для линейных схем при нулевых начальных условиях, который базируется на временном представлении свойств сигналов и электрических цепей.

1.5.1. Единичный и импульсный сигналы

При исследовании переходных процессов в линейных цепях используют эталонные воздействия, описываемые так называемыми единичными функциями. Существует воздействие в виде единичного сигнала и единичного импульса.

Единичный сигнал задается условием:

42

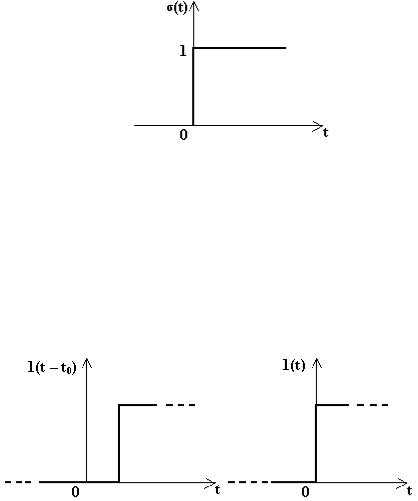
График этого воздействия в соответствии с (1.36) представлен на рис. 1.22.

Рис. 1.22. Единичный сигнал

Единичный сигнал получается из единичной ступенчатой функции Хевисайда [2]

Такое воздействие показано на рис.1.23 при t отличном от нуля и при t 0.

Рис. 1.23. Функция Хевисайда при t 0 и при t 0

Функцию Хевисайда 1t t0 удобно использовать для аналитического представления различных внешних воздей-

43

ствий на цепь, значение которых скачкообразно изменяется в момент коммутации, т.е.

Кроме единичного сигнала для анализа переходных процессов используется единичный импульс t

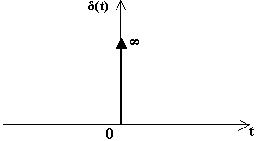
График такого воздействия в соответствии с (1.38) представлен на рис. 1.24.

Рис. 1.24. Единичный импульс

Понятие единичного импульса базируется на применении - функции или функции Дирака

44

Таким образом, импульс бесконечно малой длительности и бесконечно большой высоты, площадь которого равна 1(1.40) называется единичным импульсом. При t 0 функция Дирака обозначается как t .

С помощью - функции можно выделять значения функции f t в произвольные моменты времени t0 . Эту осо-

бенность - функции обычно называют фильтрующим свойством. Так при умножении произвольной ограниченной функции времени f t на t t0 получаем

Выражение (1.41) определяет так называемое фильтрующее свойство - импульса.

Для определения реакции линейных электрических цепей на внешнее воздействие в виде единичного скачка или единичного импульса операторным методом необходимо

45

1.5.2.Переходная и импульсная характеристики электрической цепи

Для определения свойств электрической цепи часто используют понятия переходной и импульсной характеристик. При этом цепь не должна содержать независимых источников энергии и иметь нулевые начальные условия.

Отношение реакции электрической цепи на ступенчатое воздействие к величине ступеньки при нулевых начальных условиях называют переходной характеристикой цепи h t .

Численно переходная характеристика равна реакции цепи на единичный сигнал t при нулевых начальных условиях.

Размерность переходной характеристики равна отношению размерности отклика к размерности внешнего воздействия, поэтому переходная характеристика может иметь размерность сопротивления, проводимости или быть безразмерной величиной.

Переходная характеристика h t напрямую связана с

где U1 p - входное воздействие, а U2 p - отклик (реакция)

на выходе цепи от внешнего воздействия U1 p . В виду того,

Импульсной характеристикой g t линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи (отклик на выходе) на воздействие бесконечно короткого импульса бесконечно большой высоты и конечной площади к площади этого импульса при

46

нулевых начальных условиях. Численно импульсная характеристика цепи равна ее реакции на воздействие единичного импульса при нулевых начальных условиях. Размерность им-

пульсной характеристики равна отношению размерности отклика цепи к произведению размерности внешнего воздействия на время. Учитывая соотношение (1.43), аналогично можно записать выражение, учитывающее взаимосвязь между переходной и импульсной характеристиками цепи, т.е.

1.5.3. Определение реакции цепи на произвольное внешнее воздействие по ее переходной и импульсной характеристикам. Интеграл Дюамеля

Будем считать, что внешнее воздействие на цепь u t можно представить в виде линейной комбинации однотипных элементарных составляющих uk t , т.е.

uвх t uk t ,

k

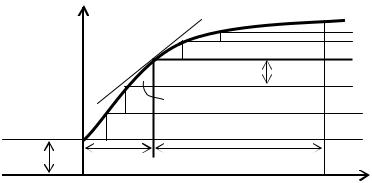
где uk t представляют собой прямоугольные неединичные скачки величиной u, смещенные относительно друг друга на величину , как это показано на рис. 1.25.

начальных условиях, т.е. это переходная характеристика цепи.

47

Составляющая отклика цепи от элементарного скачка напряжения, u, включаемого в момент времени , равна

Суммируя составляющие напряжений откликов от всех элементарных скачков, получим итоговый отклик на выходе цепи, т.е.

k

48

Переходя в (1.51) к пределу при 0, получаем замену суммирования интегрированием, т.е.

t

Выражение (1.52) известно под названием интеграла Дюамеля.

Когда под интегралом в (1.52) функция зависит только от t, то ее можно вынести, так как при интегрировании приращение происходит по .

Если функция входного воздействия описывается различными выражениями на разных интервалах времени, кроме того, имеет или не имеет скачки, то интервал интегрирования разбивается на отдельные участки, а реакция цепи, рассчитываемая интегралом Дюамеля, записывается для отдельных интервалов времени и стыкуется.

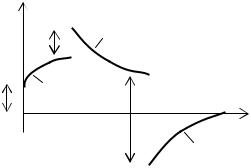
Например, в случае входного воздействия на цепь сигнала, изображенного на рис. 1.26, необходимо поступить следующим образом.

f (t)

Рис. 1.26. Входное воздействие сложной формы

В соответствии с рис.1.26 следует рассмотреть отклик цепи u t в различные интервалы времени:

49