Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методическое пособие 370

.pdf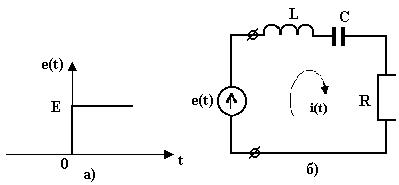

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.04 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

1.3. Переходные процессы в линейных цепях второго порядка сложности

Линейной цепью второго порядка сложности называется цепь, содержащая два независимых реактивных элемента.

Наиболее распространенными цепями второго порядка сложности являются цепи, содержащие R, L и С элементы, соединенные последовательно или параллельно.

Процессы в таких цепях описываются дифференциальным уравнением второго порядка, т.е.

a		d2 y	a	dy	a		y f t .
	2 dt2
			1 dt			0

Если в цепях первого порядка свободные процессы описываются только экспоненциальными функциями времени, то в цепях второго порядка сложности возможны кроме этого и колебательные затухающие процессы, вызванные наличием резонансных контуров.

Рассмотрим пример определения переходного процесса после подключения к последовательной RLC цепи (рис. 1.9) источника постоянного напряжения Е

0приt 0 e t

E const приt 0.

Рис. 1.9. График входного воздействия (а) и схема цепи (б)

Порядок расчета переходного процесса такой же как и для цепи первого порядка, однако, существуют свои особенности.

Так как последовательная RLC цепь содержит два независимо включенных реактивных элемента, то процессы в ней описываются дифференциальным уравнением второго порядка, а для определения двух постоянных интегрирования Ai

необходимо задать два независимых начальных условия вместо одного.

Для такой цепи независимыми начальными условиями будут:

iL (0 ) i 0 0, uc 0 uc 0 0.

Далее поступаем следующим образом.

uL uR uC e t

Используя,

второй

закон

Кирхгофа

и компонентные уравнения uL

idt,

составим

уравнение электрического равновесия в виде

idt E.

(1.10)

Дифференцируя правую и левую части (1.10), получаем

уравнение процессов в цепи после коммутации

d2i

i 0.

(1.11)

Характеристическое уравнение в соответствии с (1.11)

записанное в виде

Lp2 Rp 1/C 0,

или

0имеет два

корня, т.е.

p1,2

0 ,

(1.12)


где	R	- коэффициент затухания, 0					1	- резонансная
где		- коэффициент затухания, 0						- резонансная
	2L						LC
частота цепи.				p1 и p2
Полученные			корни	p1 и p2	уравнения			(1.11) могут
быть вещественными различными					2	02 ,		комплексно-
сопря-женными 2			02	или вещественными одинаковыми

02 , что следует из их определения (1.12). Каждому ви-

ду корней будет соответствовать свой переходной процесс.

Рассмотрим каждый из этих случаев в отдельности.

1. Вещественные различные корни. Это может произой-

ти,

когда

подкоренном выражении

(1.12)

0 ,

или

R 2

R 2 ,

, Q

что

соответствует низкой

величине

добротности

это

имеет место при R 2 .

В этом случае в соответствии с (1.5) ток ищется в виде

i i

св

A ep1t A ep2t.

(1.13)

Для определения iнеобходимо, прежде всего, найти по-

стоянные интегрирования

A1 и A2 . Для этого следует сперва

определить начальные значения тока iв цепи и его

первой

производной по

времени,

т.к. дифференциальное уравнение

idt E содержит первую производную от i

цепи L

и ток i.

Начальное значение тока цепи совпадает с начальным значением тока индуктивности, т.е. i 0 i 0 0.

Начальное значение первой производной тока цепи может быть найдено из уравнения

	di	1		t
				idt E
L		R i
	dt		c
				0
с использованием независимого				начального условия

i 0 i 0 0, и соответствующей его подстановки в него,

	di	1		t
	di	1		0dt E , что приводит к результату
т.е. L		R 0
т.е. L	dt	R 0	c
				0	di	E
					di	E	(1.14)
							(1.14)
					dt L

при t 0 , т.е. в момент времени сразу после коммутации. Постоянные интегрирования найдем из уравнения (1.13)

i A ep1t A ep2t , приравняв левую его часть нулю и приняв
1	2
t 0.	При этих условиях получим, что A1 A2	0 и это будет

первым уравнением для их определения. Второе уравнение получим, взяв первую производную от тока i (1.13) и прирав-

няв ее значение к величине E из (1.14), т.е.

	L			E
p A ep1t p		2	A ep2t	E	.
p A ep1t p			A ep2t		.
1	1		2	L
				L

При t 0 второе уравнение приводится к виду

E p1A1 p2 A2 L .

Осуществляя преобразования полученных двух уравне-

ний

A		A	0
	1	2			E
p		A p		A	E	,
p		A p		A		,
	1	1		2 2	L
					L

определяем значения A и A , т.е. A A ,										p A		p		A		E			,
определяем значения A и A , т.е. A A ,										p A		p		A					,
				1	2		1		2	1	1		2	1			L
A A ,		A p p			E	, A	E		, A					E				.
A A ,		A p p				, A	L p p		, A			L p p						.
2	1	1 1	2		L 1		L p p	2		2		L p p			2
							1	2					1		2

		Подставляя					значения			p			2 2	и
										1			0
p	2		2 2			в A и A , получим, что
	2			0			1		2
		A1			E			,	A2		E	.		(1.15)

										2L 2 02
				2L 2 02						2L 2 02

После подстановки значений (1.15) в выражение для то-

ка (1.13)

i A ep1t

A ep2t

имеем, что

ep1t

ep2t

(1.16)

2L 2 02

Исходя из (1.16) график тока (рис. 1.10) состоит из раз-

ности двух экспоненциальных токов i1 и i2 , но так как p1 p2 (см.(1.12)), то результирующий ток на графике идет

вверх. Переходной процесс в этом случае называется апериодическим и возникает при условии R 2 .

Рис. 1.10. График тока при апериодическом процессе (R 2 )

2. Комплексно-сопряженные корни. Такие корни полу-

чаются

из

уравнения

(1.12)

2 2

когда

1,2

После подстановки значений и 0

получаем,

что

, R 2

, R 2 , т.е. выражение R 2 явля-

p1,2

j св ,

ется

условием

получения

двух

корней

где

св

02 2

- частота свободных колебаний (см.1.12). Ток в

этом случае определяется уравнением i A ep1t

A ep2t ,

как и

в предыдущем примере и соответственно

L p p

Подставляя новые значения корней, получаем

L p p

L j

jL 2

св

L p1

jL2 св

Значение

тока

определяется

из

выражения

i A ep1t

A ep2t ,

после подстановки в него величин A ,

A ,

p1 и p2 , т.е.

ep1t ep2t

ep1t

ep2t =

jL2 св

e j св t

e t

ej свt

e j свt

jL2 св

свL

sin свt , т.к.

ej свt e j свt

sin свt .

свL

Таким образом, получаем, что

sin свt I0me

sin свt Im

t cos

свt

, так

свL

t Ee t / свL

e t

что Im

I0me

(1.17)

свL

где 1 2L.

Как видно из (1.17), ток представляет собой затухающую гармоническую функцию времени (рис. 1.11).

I0m	E	i
		I

свL		1m

I2m

t1+T0

I0m

св

Рис. 1.11. График тока при комплексно-сопряженных

корнях (R 2 )

Амплитуда огибающей тока i

равна

Im t I0me

(1.18)

и убывает по закону e

Скорость убывания амплитуды колебаний тем больше, чем меньше постоянная времени . Если в (1.18) вместо t подставить , то получим, что

Im	I0m	I0m	0,37I	0m.	(1.19)
		2,718
	e

Следовательно, из (1.19) можно сделать вывод, что постоянная времени контура численно равна времени, в течение которого амплитуда свободных колебаний уменьшается на 63 % от своего начального значения.

Для характеристики скорости процесса затухания свободных колебаний кроме постоянной времени используют еще логарифмический декремент затухания , который определяется как натуральный логарифм отношения тока I1m в ка-

кой-то момент времени t1 к амплитуде тока I2m

через период

свободных колебаний T0,

т.е.

t1 To

t T

I1m

I0me

lne

I2m

I0me

lne

(1.20)

Умножив числитель и знаменатель дроби (1.20) на 2Im2

с учетом значения 2L/Rполучим, что

T 2I

T R 2I2

R T

2I1m

2L 2I1m

LI1m

т.е. логарифмический декремент затухания показывает, какая часть энергии, имеющаяся в контуре в данный момент времени t1 WL расходуется в течение ближайшего полупериода свободных колебаний T0 /2 на активном сопротивлении по-

терь контура R , на котором выделяется энергия WR.

Через параметры колебательного контура величина

определяется, если учесть, что T0 2 LC и 2LR, т.е.

2 LC R

3. Случай кратных корней. Такие корни возникают, ко-

гда

в выражении (1.12)

1,2

, что

возможно,

когда

R 2

1,2

R 2 . Отсюда общее решение берется по выражению из п.1.2, т.е.

yсв A1 A2t A3t2 Antn 1 ePкt

и может быть записано при наличии двух кратных корней как i iсв A1 A2t e t . (1.21)

Порядок определения i такой же, как и при двух действительных разных корнях. Начальные условия те же, т.е.

iL 0	iL 0	0, а	di	E	.

			dt L

Постоянные интегрирования находятся аналогично. Для этого в выражении (1.21), исходя из начальных условий, бе-

рется i 0, t

и тогда 0 A1

0 1 и далее

A1 0.

Из условия

находим,

A , используя выражение

(1.21) для i, т.е.

A1e t A2te t

A1 e

A2 t e

Ввиду того, что A1 0, получаем

A2 t e

A2 e

A e t

A e tt

	Далее принимаем				во внимание,				что t	0и тогда
A	E	. С учетом (1.21) и значений A и							A ,ток	i определя-
A		. С учетом (1.21) и значений A и							A ,ток	i определя-
2	L					1			2
ется выражением							E
		i i	св	A	A t e t		E	te t .		(1.22)
		i i		A	A t e t			te t .		(1.22)
				1	2		L
							L

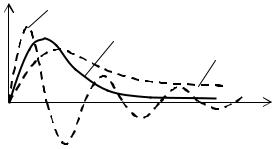
Исходя из (1.22) видно, что при одинаковых (кратных) корнях переходный процесс в цепи имеет апериодический характер, как и при различных вещественных корнях. График переходного процесса показан на рис. 1.12, при R 2 .

R<2

R=2	R >2Ρ
Ρ	R >2Ρ
0	t

Рис. 1. 12. Графики тока при разных корнях

Режим работы цепи для кратных корней при условии R 2 является критическим. Протекание тока в цепи осуществляется на границе между колебательным R 2 и апериодическим R 2 режимами.

1.4.Операторный метод анализа переходных процессов

1.4.1.Сущность операторного метода и его преимущества

Классический метод анализа переходных процессов применяют в основном тогда, когда исследуемая цепь имеет невысокий порядок сложности. Это связано, прежде всего, с тем, что в цепях с высоким порядком сложности требуется

<<< < Предыдущая 1 23 / 203 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.03 Mб5Методическое пособие 366.pdf
#
30.04.20221.03 Mб2Методическое пособие 367.pdf
#
30.04.20221.04 Mб2Методическое пособие 369.pdf
#
30.04.202224.44 Mб63Методическое пособие 37.doc
#
30.04.2022286.99 Кб4Методическое пособие 37.pdf
#
30.04.20221.04 Mб4Методическое пособие 370.pdf
#
30.04.20221.05 Mб6Методическое пособие 371.pdf
#
30.04.20221.06 Mб9Методическое пособие 372.pdf
#
30.04.20221.06 Mб15Методическое пособие 373.pdf
#
30.04.20221.07 Mб7Методическое пособие 374.pdf
#
30.04.20221.07 Mб2Методическое пособие 375.pdf