
Методическое пособие 370
.pdf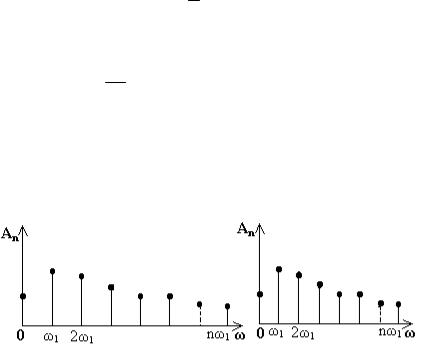
|
1 |
|
|
|
|
|
|
|
|
||
S t |
|
|
|
|
An ejn t n 1 n 1 1 |
|
|||||
2 |
|
|
|||||||||
|
|
|
n |
1 |
|
|
|
|
|
||
|
|
1 |
|
|
T |
|
|
||||
|
|
|
|
|
|
|
|
An ejn t n 1 . |
(5.19) |
||
|
|
2 |
2 |
||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
В выражении |
(5.19) |
величина n 1 n 1 n 1 1 |
|||||||||
представляет собой частотный интервал между составляющими ряда Фурье, равный частоте повторения 1 2 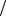 T.
T.
T
Далее, так как An 2 S t e jn tdt, то формула (5.19)
T
0
может быть записана в виде
S t 1 2
T
ejn t |
n 1 S t e jn tdt. |
(5.20) |
n |
0 |
|
По |
мере |
возрастания периода T в (5.20) интервал |
|||
n 1 |
n |
2 |
n 1 |
2 |
сокращается, и линейчатый спектр |
T |
|
||||
|
|
|
T |
||
все более сгущается (рис. 5.7).
Рис. 5.7. Сокращение интервала между составляющими спектра при увеличении периода T
130

При дальнейшем увеличении Т, когда |
T n , |
(т.е. спектр из дискретного превращается |
в сплошной), а |
n 1 d . |
|
T
Интеграл S t e jn tdt, стоящий под знаком суммы в
0
(5.20) при T принято называть спектральной функцией S j или спектральной плотностью и записывать в виде
|
|
|
S j |
S t e j tdt. |
(5.21) |
При неограниченном увеличении периода T операция суммирования в (5.20) превращается в операцию интегрирования по переменной в бесконечных пределах, т.е. теперь
|
1 |
|
|
|
S t |
S j e j td . |
(5.22) |
||
2 |
Полученное преобразование (5.22) называется обратным преобразованием Фурье функции S j (5.21), которая пред-
ставляет собой прямое преобразование Фурье функции S t . Формула (5.22) показывает, что непериодический сигнал
можно представить в виде суммы бесконечно большого числа гармонических колебаний с бесконечно малыми амплитудами, т.е. сплошным спектром.
При обратном преобразовании Фурье (5.22) интегрирование ведется по положительным и отрицательным частотам. Для прямого (5.21) и обратного (5.22) преобразований Фурье
применяют условные обозначения
S j F S t , S t F 1 S j ..
Спектральная функция S j является комплексной функцией частоты и может быть представлена в показательной форме
131

S j S e j s ,
где S - модуль спектральной функции, а s - аргумент
спектральной функции.
Выясним теперь физический смысл спектральной функции, S j , используя выражение для комплексной амплитуды
|
|
2 |
|
T |
|
|
|
An |
|
S t e jn tdt. |
(5.23) |
||
|
T |
|||||
|
|
|
|
0 |
|
|
|
При T амплитуда гармоник в (5.23) уменьшается и |
|||||
A |
dA. Коэффициент |
2 |
|
в (5.23) становится бесконечно ма- |
||
|
|
|||||
n |
|
|
T |
|
|
|
|
|
|
|
|
|
|
лым и его можно заменить дифференциалом частоты, т.е.
2 |
|
2 |
|
2 |
|
d |
. |
|
2 / |
2 |
|
||||
T |
|
|
|
||||
Величина, n . Таким образом, получаем, что
|
d |
|
|
|
|
1 |
|
|
|
|
|
S t e |
j t |
dt |
|
j t |
dt |
|
|||
dA |
|
|
S t e |
|
d |
|||||
|
|
|
|
|
|
|
|
|
|
|
1 S j d ,
или
|
S j |
|
|
dA |
|
d . |
(5.24) |
|
|||
Запишем выражение (5.24) в виде
dA e j |
1 |
S e j s d . |
(5.25) |
|
|||
|
|
|
|
Из (5.25), приравнивая модули и аргументы комплексного выражения получаем, что
dA |
1 |
S d , |
(5.26) |
|
|||
|
|
||
s . |
(5.27) |
||
132
Формулы (5.26) и (5.27) определяют что S - закон распределения амплитуд гармоник (огибающая), а s - закон
распределения начальных фаз гармоник в спектре непериодического сигнала. Выражение для спектральной функции из (5.26) можно представить в виде как
S |
dA |
|
dA |
|
1 |
|
dA |
. |
(5.28) |
|
d2 f |
|
|
||||||
|
d |
2 |
|
df |
|
||||
Из (5.28) получаем, что размерность спектральной функции S j :
S j амплитуда,
Гц что соответствует другому ее определению как спектральной
плотности сигнала, которая с физической точки зрения может быть интерпретирована как величина амплитуд спектральных составляющих, приходящихся на единицу частоты в сплошном спектре непериодического сигнала.
5.4. Зависимость между спектром и параметрами сигнала
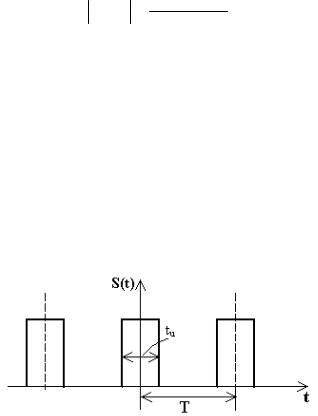
Определение этой зависимости проведем на примере рассмотрения спектра периодической последовательности прямоугольных импульсов с длительностью tu и скважностью
N T tu (рис. 5.8).
tu (рис. 5.8).
Рис. 5.8. Периодическая последовательность прямоугольных импульсов
133
Расчет комплексной амплитуды для этой последовательности согласно (5.18) приводит к выражению для ее модуля в виде
|
|
|
|
|
sin |
n |
|
|
|
|
||
A |
|
2 |
|
|
N |
|
|
, |
(5.29) |
|||
|
|
|
|
|
||||||||
|
|
|
||||||||||
|
|
|
n |
|
|
|
||||||
n |
|
N |
|
|
|
|
|
|||||
N
где n - номер гармоники.
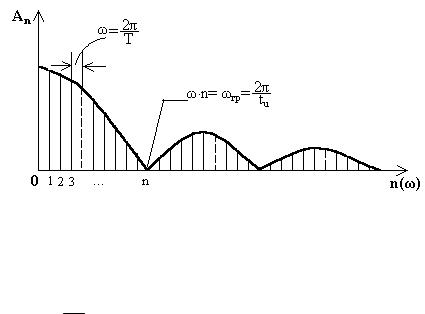
Используя зависимость (5.29) построим спектр периодической последовательности прямоугольных импульсов (рис.5.9), воспользовавшись выражением y sin x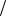 x.
x.
Рис. 5.9. Спектр периодической последовательности прямоугольных импульсов
Огибающая спектра (рис. 5.9) пересекает ось, когда вели-
чина sin n 0, что следует из формулы (5.29). Ближайшее
N
пересечение произойдет, когда величина n N 1. Отсюда по-
N 1. Отсюда по-
лучаем выражение для граничной частоты спектра fГр , осу-
ществляя преобразования, т.е.
134

n N 1, |
N T tu , |
n N, |
ntu T, |
ntu 2 , |
|||||
n |
2 tu , nf |
|
1 |
и |
fГ р |
|
1 |
. |
(5.30) |
|
|
||||||||
|
|
|
tu |
|
|
tu |
|
||
Полученные формулы позволяют осуществить анализ изменения спектра при различных вариациях параметров сигнала.
Из условия пересечения огибающей спектра с осьюn N 1 можно заключить, что чем больше скважность, N, тем большее число спектральных линий (с уменьшением величины An ) размещается под первым лепестком огибающей
N 1 можно заключить, что чем больше скважность, N, тем большее число спектральных линий (с уменьшением величины An ) размещается под первым лепестком огибающей
спектра, что наглядно продемонстрировано на рис. 5.10.
Из показанных зависимостей (рис. 5.10) следует также, что при T неограниченно увеличивается N и расстояние между возросшим числом гармоник n стремится к нулю, что приводит к понятию о сплошном спектре, рассмотренном ранее в п.п. 5.3.
Изменение длительности импульса tu ,как следует из зави-
симости (5.30), влияет как на изменение числа гармоник под лепестком огибающей, так и на значение граничной частоты спектра fГр .
Так с уменьшением tu граничная частота спектра расши-
ряется с одновременным возрастанием числа гармоник под лепестками.
Выбор определения граничной частоты по первому пересечению огибающей спектра с осью, связан с тем, что, как показывают расчеты, под первым лепестком сосредоточены составляющие спектра, определяющие около 95 % энергии сигнала, и поэтому они также определяют значение его ширины спектра.
Свойства спектра в зависимости от параметров сигнала определяются следующими теоремами [10]:
1. Увеличение амплитуды колебания S t в а раз приводит к увеличению в а раз амплитуд составляющих спектра
135
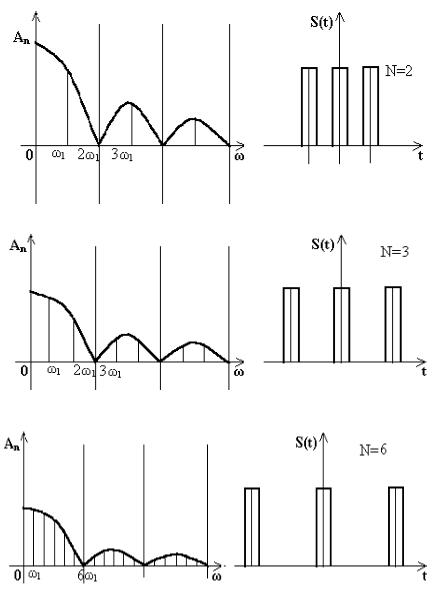
Рис. 5.10. Спектр сигнала при различной скважности N
F aS t aS j .
136

2. Задержка колебания на время эквивалентно умноже-
нию его спектра на множитель e j
F S t S j e j ,
т.е. при изменении начала отсчета времени на величину фазовый спектр сигнала изменяется (сдвигается) на , а амплитудный спектр сигнала остается неизменным;
3. Дифференцирование колебания эквивалентно умножению его спектра на j
F dSdtt j S j .
4. Интегрирование колебания эквивалентно делению его спектра на j
|
|
t |
|
j |
|
|
|
|
|
|
|
|
F S d S |
j . |
|
|
|
||||
|
|
|
|
|
|
|
|
S1 t в а раз |
||
5. При изменении масштаба времени сигнала |
||||||||||
изменяется его спектр, т.е. при |
|
1 |
|
|
|
|||||
S |
|
t S at , |
имеем S |
j |
S |
|
||||
|
|
|
|
|
. |
|||||
|
a |
|
||||||||
|
2 |
1 |
2 |
|
|
1 |
a |
|||
Если a 1, |
то S2 t сжат относительно S1 t в а раз и при |
|||||||||
этом спектр S2 j растянут относительно S1 j в а раз. |
||||||||||
Когда a 1 |
S2 t растянут относительно |
S1 t |
в а раз и |
|||||||
спектр S2 j сжат относительно S1 j в а раз. |
|
|
|
|||||||
Одновременно с растяжением спектра происходит уменьшение амплитуд его спектральных составляющих в а раз, а при сжатии спектра – увеличение их в такое же количество раз.
137
5.5. Распределение мощности в спектре сигнала
В случае периодического сигнала среднее за период значение мощности определяется выражением
|
|
|
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
|
P |
|
p t dt, |
|
(5.31) |
||
|
|
|
|
|
|
|
|
T |
|
|||||
|
p t S2 t /R |
|
|
0 |
|
|
||||||||
где |
|
мгновенная активная мощность сигнала |
||||||||||||
S t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При R 1 Ом получим из (5.31), что |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
|
P |
S2 t dt. |
|
(5.32) |
|||
|
|
|
|
|
|
|
|
T |
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
|
На основании преобразования Фурье (5.11) можно запи- |
|||||||||||||
сать, что |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
t |
A |
|
|
A cos n t |
|
||||||
|
S |
|
0 |
|
|
|
|
(5.33) |
||||||
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
n |
n |
|
||||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
||
|
При возведении выражения (5.33) в квадрат с учетом, |
|||||||||||||
что |
cos2 1 cos2 2 |
|
и подстановки его в (5.32) все со- |
|||||||||||
ставляющие с косинусами при интегрировании за период будут равны нулю, и поэтому получим, что
2 |
2 |
|
|||
P |
A0 |
|
An |
, |
(5.34) |
4 |
2 |
||||
n 1
Откуда средняя за период мощность периодического сигнала равна сумме средних мощностей постоянной составляющей и всех его гармоник.
Записав выражение (5.34) в виде
1 |
T |
2 |
2 |
|
||
S2 t dt |
A0 |
|
An |
, |
(5.35) |
|
T |
4 |
2 |
||||
0 |
|
n 1 |
|
|||
138
получим соотношение известное как равенство Парсеваля. Равенство Парсеваля (5.35) показывает, что средняя за
период мощность периодического сигнала не зависит от начальных фаз его гармоник.
Для непериодического сигнала аналогично равенству Парсеваля (5.35) при T может быть доказано равенство Релея [10]
S2 t dt |
|
1 |
S2 d . |
(5.36) |
|
||||
|
|
|
0 |
|
Равенство Релея (5.36) показывает, что полную энергию непериодического сигнала можно определить путем интегри-
рования либо функции S2 t во временной области, либо
S2 в частотной области.
5.6.Спектральное представление единичного сигнала
иединичного импульса
Рассмотрим сначало, как с помощью спектрального описания можно представить рассмотренный ранее (1.36) единичный сигнал
1 приt 0
t
0 приt 0.
Определим спектральную плотность единичного сигнала. Заметим, что в связи с тем, что этот сигнал не удовлетворяет условию абсолютной интегрируемости, то его спектральную плотность нельзя непосредственно определить путем прямого преобразования Фурье по формуле (5.21), т.е.
S j S t e j tdt.
Воспользуемся для этого преобразованием Лапласа
(1.4.3). Известно (1.4.2), что
139
