
Методическое пособие 370
.pdf7. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕМЕ «СПЕКТРЫ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ»
Контрольные вопросы
1.Докажите ортогональность гармонической базисной системы функций. Является ли гармонический базис ортонормированным?
2.Запишите формулы для определения коэффициентов гармоник ряда Фурье. Какие формы ряда Фурье используются для представления периодического процесса?
3.Как определить частоту первой и других гармоник периодического процесса?
4.Как определить уровень постоянной составляющей периодической последовательности импульсов?
5.Как выделить постоянную составляющую и гармонические составляющие из периодического процесса?
6.Что называется амплитудным спектром? Каким образом строят такой спектр?
7.Что называется фазовым дискретным спектром? Каким образом строят такой спектр?
8.Как зависит амплитудный спектр периодической последовательности импульсов от их длительности и периода следования?
9.Что понимается под шириной спектра периодического процесса и как определить его по известной, например, длительности прямоугольного импульса?
10.Что такое непериодический сигнал и как его можно получить из периодического процесса?
11.Какой характер спектра (линейчатый, сплошной) имеет одиночный импульс и можно ли охарактеризовать его свойства посредством спектра амплитуд и спектра фаз?
12.Посредством какой функции могут быть представлены частотные свойства одиночного импульса?
13.Что такое прямое и обратное преобразования Фурье?
170
14.Каков физический смысл спектральной функции и что представляет собою по определению размерность спектральной плотности амплитуд одиночного сигнала?
15.Какими теоремами определяются свойства спектра сигнала
взависимости от изменения его параметров?
16.Как определяется мощность периодического и непериодического сигналов через их спектры?
17.Как можно с помощью спектрального представления охарактеризовать свойства единичного сигнала и единичного импульса?
18.Каким образом можно определить реакцию цепи на негармоническое воздействие с помощью спектрального метода?
19.Какие требования необходимо предъявить к свойствам электрической цепи для передачи через нее сигналов без искажений?
7.1.Задачи для самостоятельного решения
7.1.1.Напишите зависимость, выражающую пятую гармонику сигнала u t в тригонометрической форме, если известно
из спектра амплитуд и спектра фаз, что интервал между спектральными линиями равен f 1Мгц, амплитуда пятой гармоники U5 10 В, 5 0,3 рад.
7.1.2.Определите мощность пятой гармоники из задачи 7.1, если напряжение u t действует на сопротивление в 1 Ом.
7.1.3.Определите, какой приблизительно полосой пропускания должен обладать линейный усилитель, чтобы обеспечить усиление без искажений прямоугольных импульсов с
длительностью u 1 10 3 с?
7.1.4. Определите формулы для коэффициентов an и bn ,
если вместо переменной t для сигнала S t использовать переменную в радианной мере t и период 2 рад.
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
S cosn d , |
|
|
||||
Ответ: an |
bn |
|
S sin d . |
|||||
|
|
|||||||
|
|
|
|
0 |
||||
|
|
0 |
|
|
|
|
|
|
171

7.1.5. Разложить в тригонометрический ряд Фурье периодическую функцию (рис.7.1), получаемую при однополупериодном "выпрямлении" косинусоидыs(t)=cos t при - /2 t /2.
|
|
|
|
|
Рис. 7.1 |
|
|
|
||
1 |
|
|
2 |
|
2 |
|
||||
Ответ: s(t) |
|
1 |
|
|
cos t |
|
|
cos t |
|
cos4 t |
|
|
|
|
|||||||
|
|
2 |
3 |
|
15 |
|
||||
7.1.6. Используя комплексную форму разложения периодического процесса в ряд Фурье, определить спектр сигнала (рис. 7.2), задаваемый аналитическим выражением
1, |
при |
0 t |
s(t) |
при |
t 2 . |
1, |
Рис. 7.2
Ответ: s(t) |
4 |
sin t |
4 |
sin3 t |
4 |
sin5 t |
|
|
|
||||
|
|
3 |
5 |
|||
172
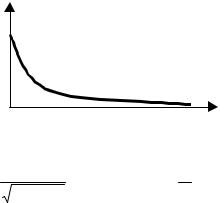
7.1.7. |
Определить |
спектральную |
функцию |
импульса |
|||
(рис.7.3), который задается следующим выражением |
|
||||||
|
|
|
at |
при |
t 0 |
|
|
|
|
|
e |
|
|
||
|
|
s(t) |
|
|
|
|
|
|
|
|
|
при |
t 0. |
|
|
|
|
|
0 |
|
|
||
|
s(t) |
|
|
|
|
|
|
|
|
|
Рис. 7.3 |
t |
|
|
|
|
|
|
|
|
|
||
Ответ: |
s(t) |
1 |
, s ( ) arctg . |
|
|
||
|
a2 |
2 |
|
a |
|
|
|
7.1.8. Задаваясь конкретными параметрами сигнала из за- |
|||||||
дачи 7.1.5, построить его амплитудный и фазовый спектры с |
|||||||
помощью программы Mathcad, изменив параметр t на t |
и |
||||||
интегрируя в пределах от 0 до T , при Um 1 В, |
T 0.005 |
и |
|||||
t : 0, 0.00001...0.005. |
|
|
|
|
|
|
|
7.1.9.Осуществить определение спектра сигнала из задачи
7.1.6посредством программы Workbench. Сравнить результаты моделирования с расчетными значениями, полученными ранее.
7.1.10.Решить задачу 7.1.5, используя быстрое преобразование Фурье (БПФ) из программы Mathcad.
7.2.Примеры решения задач
7.2.1.Разложить в тригонометрический ряд Фурье знакопеременную прямоугольную функцию (рис. 7.4), определяемую выражением
1, |
при |
0 t |
s(t) |
при |
t 2 . |
1, |
173

Рис.7.4
Решение
Обозначим через величину t, т. е. t= и запишем выражение для спектра функции в виде
|
a0 |
|
|
s( ) |
an cosn bn sinn . |
||
|
|||
2 |
n 1 |
||
Ввиду того, что функция s( ) симметрична относительно горизонтальной оси, то в спектре будет отсутствовать постоянная составляющая, т. е. а0/2=0.
С учетом несимметричности s( ) относительно вертикальной оси получаем, что аn=0, т. е. в спектре сигнала не будет косинусоидальных составляющих.
Определим коэффициент bn, используя формулу
1 2
bn S( ) sinn d .
0
Учитывая значения, принимаемые функцией S( ), находим, что
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
bn |
|
|
1 sinn d 1 sinn d |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
1 |
cosn |
|
|
|
1 |
cosn |
|
2 |
|
1 2 |
|
2 |
cosn |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
0 |
|
n |
|
|
|
|
|
|
n |
|
|
||||||||
|
2 |
|
|
1 cosn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n
174

Придавая n значения 1,2,3 и т.д., получаем, что
b |
|
4 |
; b |
0; b |
|
4 |
и т.д. |
|
|
||||||
n 1 |
|
n 2 |
n 3 |
|
3 |
||
Таким образом, функция S( ) может быть представлена выражением
|
4 |
|
4 |
|
4 |
|
|
S( ) bn sin |
sin t |
sin3 t |
sin5 t . |
||||
|
|
|
|||||
n 1 |
|
3 |
5 |
||||
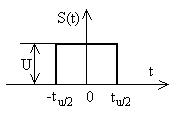
7.2.2. Используя комплексную форму разложения периодического процесса в ряд Фурье, определить спектр сигнала (рис.7.5), определяемый выражением
1 |
0 t t1 |
|
T 2t1. |
S(t) |
|
|
t1 t 2t, |
0 |
Рис. 7.5
Решение
Определяем комплексную амплитуду Аn сигнала S(t) с уче-
том, что T=2t1, как
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
T |
|
2 |
T |
|
|
2 |
2 |
|
|
2 |
|
|
1 |
|
|
2 |
|
|
e |
jn 1t |
|
e |
jn 1t |
|
|
jn 1t |
|
|||||||
|
|
|
|
|
|
|||||||||||
An |
|
|
dt |
|
|
|
|
|
|
|
|
e |
|
|
||
T |
|
T |
|
T |
jn |
|
||||||||||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
175

T2 jn1 1 e jn 1T2 1 .
Принимая во внимание, что 2 , получаем, что
|
|
Т |
An |
1 |
1 e jn . |
|
||
|
jn |
|
Используя выражение е-jn =cosn -j·sinn , и принимая во внимание, что sin n =0 для n=1,2,3,…,получим, что для нечетных n
An 2 . jn
Комплексный ряд Фурье для сигнала будет иметь вид
|
1 |
|
|
1 |
|
2 |
|
S(t) |
|
Anejn t |
|
|
|
|
ejn t . |
2 |
2 |
jn |
|||||
|
|
n |
|
|
n |
|
|
В тригонометрической форме спектр сигнала записывается
как
|
A0 |
|
|
|
|
|
|
|
|
|
jn t |
||
S(t) |
|
R |
|
|
A e |
. |
|
|
|||||
2 |
e |
n |
|
|||
|
|
|
n 1 |
|
|
|
Постоянная составляющая сигнала определяется по формуле, с учетом, что n=0
T T /2
A20 T1 e jn tdt T1 1 dt 12 .
0 0
Составляющие спектра сигналаопределяются как
176
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
j |
|
|
|
|
|
|
|
|
|
|
2 |
|
j n t |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
An Re An ejn t Re |
|
e |
2 ejn t |
Re |
|
|
|
e |
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
R |
|
|
cos n t |
|
|
|
j sin n t |
|
|
|
|
|
|
|
|
sin n t . |
|
|
|
|
||||||||||
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||||||
e |
n |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
При n=1, 3, 5, 7, … получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
S(t) |
1 |
|
|
2 |
sin t |
2 |
sin 3 t |
2 |
|
|
sin 5 t . |
|
|||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7.2.3. Определить спектральную функцию одиночного прямоугольного импульса (рис.7.6).
Рис. 7.6
Построить график спектральной функции.
Решение
Для определения спектральной функции S(j ) воспользуемся формулой (5.21)
S(j ) S(t) e j tdt .
С учетом того, что импульс симметричен относительно вертикальной оси, получим, что
177

|
tu /2 |
tu / 2 |
1 |
|
|
S(j ) |
S(t) e j tdt |
U e j tdt U |
e j t |
||
j |
|||||
|
tu / 2 |
tu /2 |
|
|
tu /2
tu /2
|
U |
j |
tu |
|
j |
tu |
|
|
|
|
|
||||
|
|
e 2 |
e |
|
2 . |
||
|
|||||||
|
j |
|
|
|
|
||
|
|
|
|
|
|
|
|
Умножив и разделив полученное выражение на j2, и применив формулу Эйлера для sin , найдем, что
|
|
|
|
j |
tu |
|
j |
tu |
|
|
|
|
|
|
|
|
U j2 e |
2 e |
|
2U |
|
t |
|
|
|||||||
S(j ) |
|
2 |
|
|
|
u |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
sin |
|
. |
||
|
|
|
|
j2 |
|
|
|
|
|
|
|||||
|
j |
|
|
|
|
|
|
2 |
|
||||||
После преобразования этого выражения получим, что
|
2U |
|
tu |
sin |
tu |
|
|
|
|
|
|
|
sin tu |
/2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
S(j ) |
|
2 |
|
Utu |
|
B j0 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
t /2 |
|
|
|
t |
u |
/2 |
|
|||||||||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Запишем полученное выражение в виде |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
S(j ) A e j ( ) |
|
|
|
|
|
|
|
|
|
e jarctg |
|
, |
||||||||||||
|
|
|
B2 02 |
|
||||||||||||||||||||
|
|
|
B |
|||||||||||||||||||||
где А – модуль S(j ), а ( ) – фазовая характеристика. |
||||||||||||||||||||||||
Таким образом, получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
tu |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А Utu |
|
|
2 |
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
tu |
/2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Начальные фазы гармоник будут определяться законом
функции sin tu , т.е. 2
|
0 |
|
|
|
|
arctg |
|
|
при |
B 0 |
|
|
|||||
|
B |
|
|||
s |
0 |
|
|
||
|
|
|
|||
arctg |
|
|
при B 0. |
||
|
|
|
B |
|
|
|
|
|
|
||
178
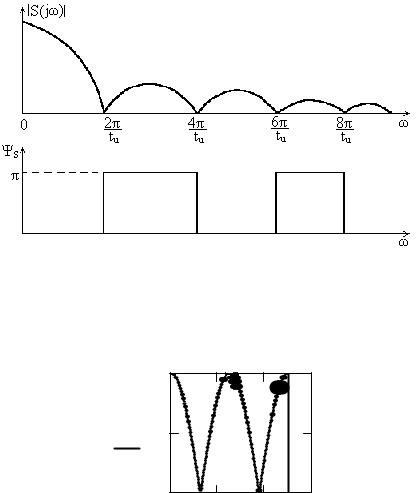
Графики модуля S(j ) и фазовой характеристики s пред-
ставлены на рис. 7.7.
Рис. 7.7
7.2.4. Используя программу Mathcad, определить спектр колебания S t , получаемый при двухполупериодном «выпрямлении» косинусоидального сигнала u t cos t (рис.7.8).
|
1 |
|
|
|
u(t) |
0.5 |
|
|
|
|
0 |
0.002 |
0.004 |
0.006 |
|
0 |
|||
|
|
|
t |
|
|
|
Рис. 7.8 |
|
|
179
