3. Моделирование конструкции пресс-формы для изготовления экрана из сверхпроводящего материала

При изготовлении экрана из материала, обладающего сверхпроводимостью, заготовку получают методом прессования из порошка. Усилия, необходимые для обеспечения технологического процесса, достигают достаточно высоких значений.

Детали пресс–формы находятся в сложном пространственном напряженно-деформированном состоянии. Наиболее напряжёнными деталями пресс-формы являются матрица и пуансон (рисунок 70).

В литературе [10] приводятся формулы для расчета толщины стенки круглой матрицы (гильзы наружной).

Вычисление действительных напряжений в деталях пресс-формы аналитическими методами затруднено, поэтому приведенные зависимости являются приближенными.

Наиболее детальное исследование напряженно-деформированного состояния пресс-формы возможно только при использовании современных численных методов, среди которых самым развитым является метод конечных элементов (МКЭ) [11].

Постановка задачи предусматривает исследование напряженно-деформированного состояния пространственной линейно-упругой конструкции пресс-формы, статически нагруженной равномерно распределенными силами от прессуемого порошка и усилия пресса.

Для обеспечения технологического процесса требуется приложить осевое усилие к пуансону величиной Q =200 кН. В соответствии с этим, интенсивность осевой равномерно распределенной нагрузки на пуансон и матрицу равна

, (49)

где Q – осевое усилие, кН; F_п – площадь поперечного сечения пуансона.

Рисунок 70 – Конструктивная модель пресс-формы: 1 – матрица; 2 – пуансон

Боковое давление на стенки матрицы определяется в соответствии с [10] по формуле

Р_б=0,25Р (50)

Конструктивная модель, исследуемой пресс-формы, представлена на рисунке 70. Построение конечно-элементной модели предусматривает использование объемных элементов в форме призмы с треугольным основанием. Получение матрицы жесткости такого элемента описано в [11]. Каждый узел такого элемента имеет 3 степени свободы: линейные перемещения вдоль осей глобальной системы координат. Учитывая симметричность конструкции и нагружения, выполнено также моделирование пресс-формы с использованием осесимметричных конечных элементов.

Дискретная модель пресс-формы состоит из 15660 объемных конечных элементов, объединенных 9964 узлами (число узловых степеней свободы равно 29892). На рисунке 71 представлены конечно-элементные модели матрицы и пуансона, исследуемых с использованием объемных элементов в форме прямой треугольной призмы.

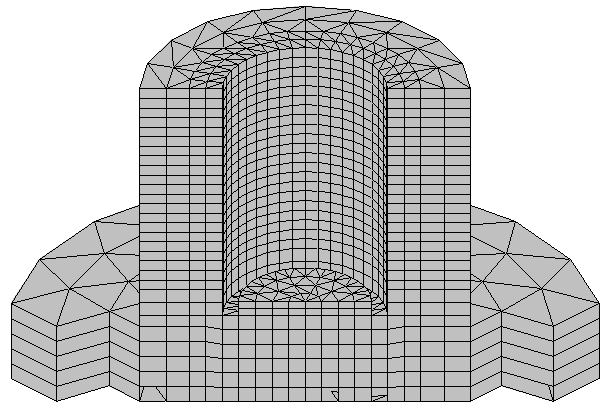
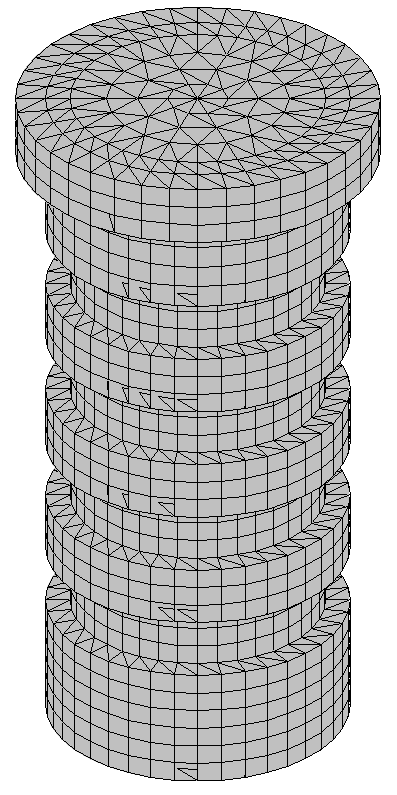
Рисунок 71 – Сетка конечных элементов матрицы и пуансона

Граничные условия запрещают все степени свободы узлов нижней опорной плоскости матрицы, для пуансона введены закрепления, препятствующие его перемещению как жесткого целого.

Эпюра распределения эквивалентных напряжений в конечных элементах матрицы (рисунок 72) и пуансона (рисунок 73).

Зона наибольших напряжений расположена в нижней части внутренней цилиндрической поверхности матрицы (уровень напряжений достигает 90 МПа); в верхней части пуансона возникают наибольшие напряжения на внутренних канавках ( уровень напряжений 155 МПа).

Картина распределения узловых перемещений вдоль осей ОX, OY глобальной системы отсчета представлена на рисунках 74, 75.

Наибольшее перемещение вдоль оси OX имеют узлы матрицы, расположенные внутри нижней части ее (перемещение равно 0.0029мм).

Эпюры узловых перемещений пуансона вдоль осей OX, OY показаны на рисунках 76, 77. Максимальные перемещения узлов, расположенных в нижней части пуансона вдоль оси OX достигают величины 0.0026мм.

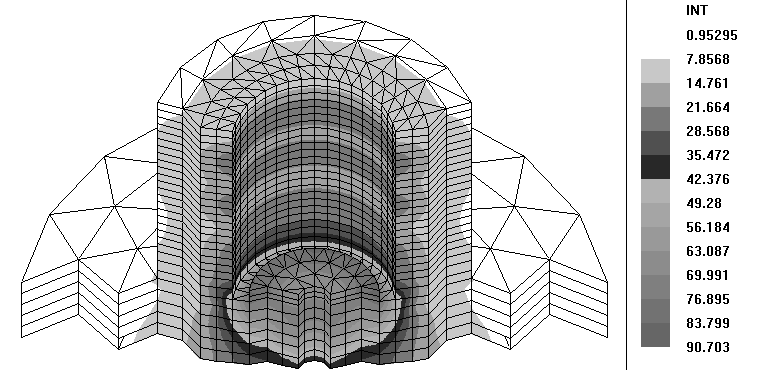
Рисунок 72 – Эпюра эквивалентных напряжений в элементах матрицы

Рисунок 73 – Эпюра эквивалентных напряжений в элементах пуансона

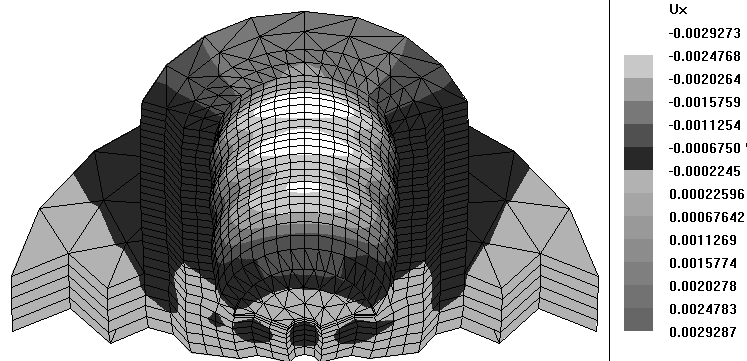
Рисунок 74 – Узловые перемещения матрицы вдоль оси OX

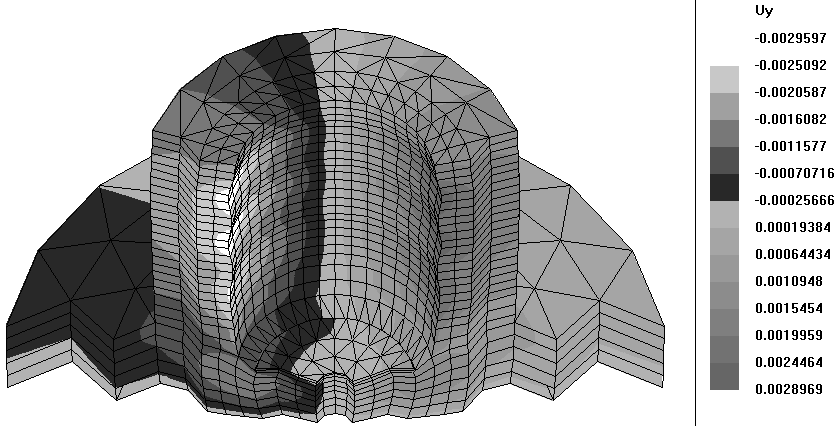
Рисунок 75 – Узловые перемещения матрицы вдоль оси OY

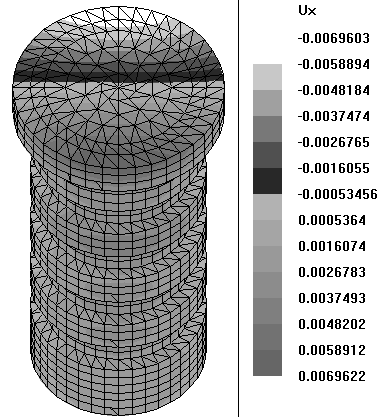
Рисунок 76 – Узловые перемещения пуансона вдоль оси OX

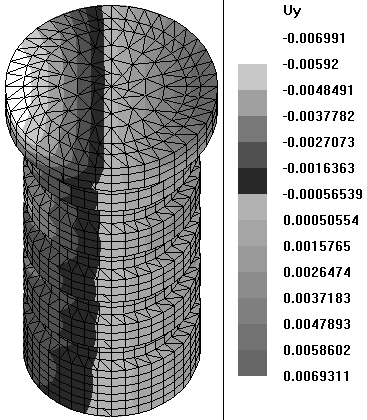
Рисунок 77 – Узловые перемещения пуансона вдоль оси OY