1. Плоская задача теории упругости

Существует широкий класс важных в практическом отношении задач, в которых перемещения, деформации и напряжения зависят лишь от двух координат — x и y. Этот класс задач под общим названием «плоская задача теории упругости» подразделяется на плоскую деформацию и обобщенное плоское напряженное состояние.

Если в процессе нагружения все точки тела перемещаются только параллельно одной плоскости (плоскости xy, например), то соответствующее деформированное состояние называется плоской деформацией. Таким образом, для плоской деформации имеем u_x=u_x(x,y), u_y=u_y(x,y), u_z=0.

Рисунок 39

Выделим из тела элементарный параллелепипед сечениями, параллельными координатным плоскостям (рисунок 39). Обозначим компоненты напряжения в площадке, перпендикулярной оси x, через _x, _xy, _xz, аналогично для других площадок. Первый индекс в этих обозначениях характеризует ориентацию площадки, а второй направление действия соответствующей составляющей напряжения.

В соответствии с уравнениями Коши, деформации _xz=du_x/dz+du_z/dx, _zz=du_z/dz, _yz=du_z/dy+du_y/dz оказываются равными нулю.

Из закона Гука вытекает, что касательные напряжения _xz=G_xz, _yz=G_yz также равны нулю (G — модуль сдвига,  — относительная деформация). Остальные компоненты деформации и напряжения являются функциями только координат x и y.

Если тонкая пластина, параллельная плоскости xy, нагружена объемными и по контуру — поверхностными силами, параллельными ее плоскости и равномерно распределенными по толщине, то имеет место обобщенное плоское напряженное состояние. В этом случае можно пренебречь компонентами напряжения _z, _xz и _yz, а _x, _y и _xy считать постоянными по толщине:

_z=_xz=_yz=0 _x= _x(x,y), _y= _y(x,y) и _xy= _xy(x,y).

Из закона Гука следует, что при обобщенном плоском напряженном состоянии деформации сдвига _xz=_yz=0, а остальные компоненты деформации представляются как функции только координат x и y.

2. Основные соотношения для плоского треугольного элемента

Расчет по методу конечных элементов начинается с дискретизации расчетной модели. Пусть рассматриваемая область двумерна, т.е. все ее характеристики зависят от двух координат (рисунок 40). Каждый конечный элемент этой области сохраняет все физические и геометрические свойства исходной среды. На границе области заданы граничные условия [1–4].

Рисунок 40

Для решения плоской задачи теории упругости разработано много разнообразных конечных элементов, отличающихся друг от друга аппроксимацией перемещений и способом описания геометрии. В качестве наиболее простого рассмотрим плоский треугольный элемент с тремя узлами в углах (рисунок 41). Узловые перемещения для такого элемента указаны на рисунке. Вектор перемещений для узла i состоит из двух компонент:

(3.1)

Рисунок 41

Обход узлов производится против хода часовой стрелки. Шесть компонент перемещений элемента образуют вектор:

. (3.2)

Перемещения точек внутри элемента однозначно определяются этими шестью величинами. Наиболее простым представлением являются линейные полиномы:

(3.3)

Значения шести постоянных _i можно найти из двух систем, состоящих из трех уравнений, которые получаются при подстановке в последние уравнения узловых координат и приравнивания перемещений соответствующим перемещениям узловых точек:

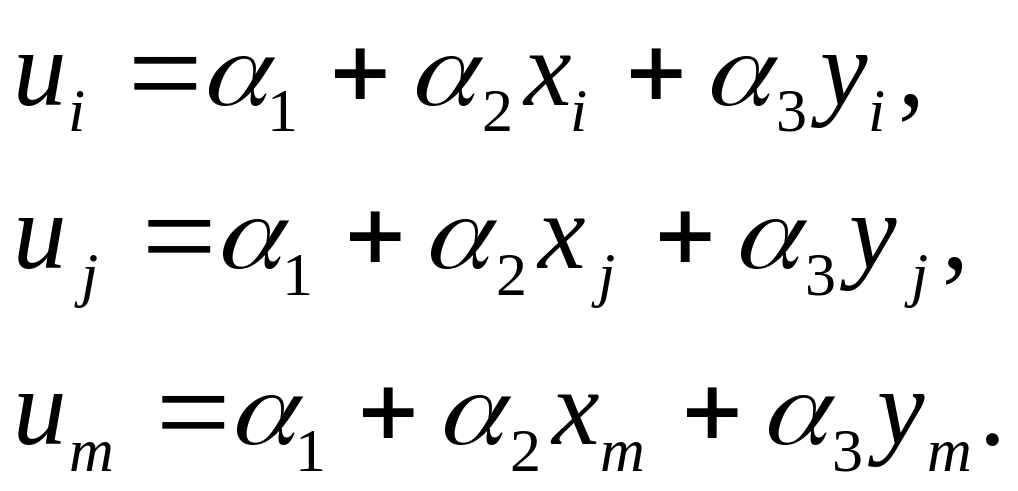(3.4)

Выражая ₁, ₂, ₃ через величины узловых перемещений, получим

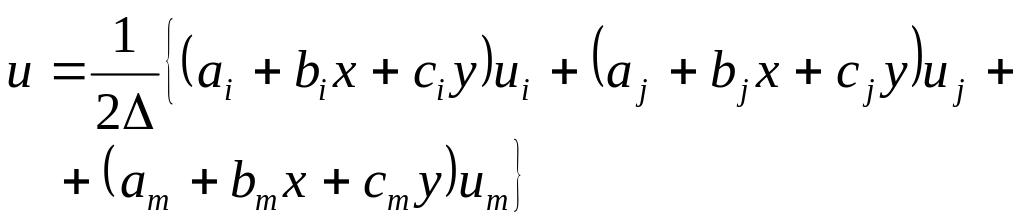, (3.5)

где (3.6)

Остальные коэффициенты получаются циклической перестановкой индексов i, j, m, а величина 2 определяется соотношением

(площадь треугольника ijm). (3.7)

Аналогично выражается перемещение v по направлению оси y:

(3.8)

В стандартной форме

(3.9)

Полную деформацию в любой точке внутри элемента можно представить тремя составляющими:

(3.10)

Используя предыдущие равенства (1.8) и (1.9), получим,

(3.11)

что определяет матрицу [B], связывающую деформации с перемещениями. Так как матрица [B] не зависит от координат точки внутри элемента, то деформации в нем постоянны.

Напряжения связаны с деформациями зависимостью:

, (3.12)

где матрица упругих постоянных для плоского напряженного состояния имеет вид

, (3.13)

Матрица жесткости элемента ijm определяется с помощью соотношения:

, (3.14)

где t — толщина элемента, а интегрирование ведется по площади треугольника. Если толщина элемента постоянна, то, поскольку ни одна из матриц не содержит x или y, получим простое выражение:

, (3.15)

где и т.д.

Матрица жесткости может быть записана в виде:

, (3.16)

Составление матрицы жесткости ансамбля элементов производится суммированием матриц жесткости конечных элементов, имеющих общие узлы.

Для конечноэлементного ансамбля можно записать:

. (3.17)

где {R} — внешние силы; {R}_p — силы, уравновешивающие действующие на элемент распределенные нагрузки; — силы в узлах, обусловленные начальной деформацией.