Учебники / Лекции по термодинамике неравновесных систем. Пармон

Отсюда

131

Пример 4

Найдем коэффициенты взаимности Онзагера для парал-

которые осуществляются по схеме

R1 1 Y1,

Y1 + R2 2 Y2, Y2 3 P1,

Y2 4 Y3 5 Y4 6 Y5 7 P2,

где Yi – интермедиаты.

132

Динамические движущие силы для брутто-реакций

Последовательный процесс, записанный в последней строке схемы превращений, можно заменить одним эффектив-

ным превращением

Обозначим

Σ = ε ε + ε ε + ε ε + ε ε + ε ~

1 2 1 3 1 эфф 2 ( 3 эфф )R2 .

133

При этом

Пример 5

Параллельные стехиометрические брутто-процессы

P1;

R1 + R2 (2.28)

P2,

осуществляются по схеме

R1 1 Y1,

Y1 + R2 2 Y2,

134

в стационарном по Y3 режиме можно заменить эффектив-

ными процессами

R1 + R2 Y2

c

135

Поэтому схему превращений (2.29) можно упростить:

R1 + R2 εэфф1 Y2,

Y2 ε3 P1,

Y2 εэфф2 P2.

Видно, что полученная схема аналогична схеме (2.14). Поэтому, следуя решению (2.17) и обозначив

Σ ≡ εэфф1 + ε3 + εэфф2 , сразу находим:

L11 = ε3 (εэфф1 + εэфф2 )Σ ,

L22 = εэфф2 (εэфф1 + ε3 )Σ,

L12 = L21 = −ε3 εэфф2 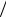Σ.

Аналогичным образом, замещая в стационарных режимах совокупности некоторых превращений эффективными превращениями, можно находить точные выражения для коэффициентов взаимности в модифицированных уравнениях Онзагера даже для очень сложных схем параллельных бруттопревращений.

Очевидно, аналогичные подходы для нахождения значений коэффициентов взаимности модифицированных уравнений Онзагера применимы и для схем с нелинейными превращениями интермедиатов.

136

§ 2.5. Термодинамические критерии достижения устойчивости стационарных состояний

При неизменных внешних условиях в неравновесной системе возможно установление стационарного состояния. Особенностью такого состояния является неизменность во времени внутренних параметров системы и как следствие отсутствие (равенство нулю) потоков внутренних термодинамических параметров, характеризующих состояние системы. Значение этих параметров определяется протеканием внутренних необратимых процессов, возбуждаемых внутренними термодинамическими силами.

Например, в стационарном состоянии открытой химически реакционноспособной системы постоянны во времени концентрации интермедиатов, устанавливающиеся за счет внутренних процессов. Таким образом, в стационарном состоянии скорость изменения концентрации промежуточных продуктовинтермедиатов (потоки этих параметров) равна нулю. Стационарное состояние системы достигается при определенных соотношениях между скоростями элементарных реакций, ответственных за образование и исчезновение интермедиатов.

Суммарная энтропия открытой системы в стационарном состоянии также постоянна, т. е. dS / dt = deS / dt + diS / dt = 0. Однако при этом члены deS / dt и diS / dt, соответствующие процессам обмена системы с окружающей средой и внутренним необратимым процессам внутри системы, могут быть отличны от нуля.

Существует взаимосвязь между скоростью производства энтропии за счет самопроизвольных необратимых процессов внутри открытой системы и установлением в ней стационарного неравновесного состояния. При этом характер измене-

ния во времени величины diS / dt во многих случаях позволяет установить наличие эволюции открытой системы к стационарному состоянию.

Данная проблема сходна с проблемой классической термодинамики о предсказании направления самопроизвольных необратимых процессов в изолированной системе: согласно

137

второму началу термодинамики, в последнем случае эти изменения происходят только в направлении увеличения энтропии. При этом в конечном равновесном состоянии энтропия достигает своего максимального значения.

Теория термодинамики неравновесных процессов позволяет также ответить и на вопрос об устойчивости неравно-

весных стационарных состояний к внешним возмущениям и самопроизвольным флуктуациям в системе, а также дает возможность исследовать эту устойчивость путем анализа изменения величины скорости производства энтропии при выводе системы из стационарного состояния.

2.5.1. Критерий эволюции (теорема) Пригожина для систем, близких к термодинамическому равновесию

Рассмотрим открытую систему, в которой одновременно протекают m необратимых процессов. Согласно выражению (2.5), скорость диссипации энергии и связанная с этим скорость производства энтропии в этой системе

P = T diS = ∑m JiXi > 0 . dt i=1

Если система находится вблизи состояния термодинамического равновесия, где справедливы линейные соотношения между значениями потоков и сопряженных им термодинамических сил, а также линейные соотношения взаимности Онза-

m

гера, то Ji = ∑Lik Xk . Поэтому значение скорости диссипации

k=1

энергии в данном случае имеет вид функционала Рэлея– Онзагера:

Суммирование здесь ведется по всем как «внутренним» (т. е. зависящим только от внутренних необратимых процессов), так и «внешним» (т. е. зависящим не только от внутренних процессов) переменным.

138

По предположению, к установлению стационарного состояния с Ji = 0 для потока внутренних параметров аi приво-

дят изменения внутренних термодинамических сил Хi. Исследуем характер зависимости величины P от силы Хi, взяв частную производную ∂P / ∂Xi при постоянных Хj (j ≠ i).

В связи с особенностью конструкции функционала Релея– Онзагера (2.12)

(∂P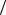∂Xi )Xj,j≠i = 2(∑Lik Xk ) = 2 Ji .

k

Следовательно, и области линейной термодинамики условие достижения стационарного состояния по некоторой внутренней переменной i (например, концентрации веществантермедиата), т. е. равенство нулю соответствующего этой переменной потока

Ji = 0 ,

и условие

эквивалентны. При этом поскольку величина P является положительно определенным квадратичным выражением во всей допустимой области изменения независимого переменного Хi, то равенство нулю производной (∂P / ∂Xi) = 0 является условием минимума функции P(Х1,Х2, ... Xm) по переменной Хi.

Аналогично получаем условия стационарности и для потоков других внутренних переменных. Например:

Таким образом, вывод об эквивалентности условий минимума функционала Р и достижения скорости справедлив для произвольной системы, в которой протекает любое количество процессов, связанных между собой линейными соотношениям взаимности Онзагера. Поэтому соотношения наподобие (2.13) и (2.14) выражают следующее важное свойство необратимых процессов в любых открытых системах, находящихся

вблизи термодинамически равновесного состояния:

139

При неизменных внешних условиях в стационарном состоянии открытой системы, близкой к термодинамическому равновесию, скорость производства энтропии является постоянной, положительной и минимальной.

Этот вывод является основным содержанием теоремы И. Пригожина (1947 г., Нобелевская премия 1977 г.). Существенно также, что по мере самопроизвольной эволюции системы к стационарному состоянию возможно лишь монотонное уменьшение величины Р, т. е.

Поэтому принцип минимума скорости производства эн-

тропии является количественным критерием для определения направления самопроизвольных изменений в открытой системе, т. е. критерием ее эволюции. В изотер-

мической системе принцип минимума скорости производства энтропии полностью эквивалентен принципу минимума скорости диссипации энергии, сформулированному Онзагером в 30-е гг. ХХ в. (Нобелевская премия 1968 г.) при рассмотрении частных задач электродинамики.

Если система находится вблизи равновесия, то характер изменения скорости прироста энтропии (или скорости «диссипации энергии») позволяет обнаружить переход системы в стационарное состояние. В самом деле, по мере движения системы из некоторого исходного состояния к стационарному состоянию величина P = TdiS / dt монотонно уменьшается.

Однако значение P остается при этом положительным и постепенно приближается к минимальному постоянному положительному значению, которое отвечает достижению конечного стационарного состояния. Таким образом, выражение

(2.15) является критерием эволюции системы к стацио-

нарному состоянию вблизи термодинамического равновесия.

Справедливость критерия эволюции Пригожина легко подтверждается прямым анализом эволюции систем с большим числом обратимых химических процессов вблизи их термоди-

140