
Учебники / Лекции по термодинамике неравновесных систем. Пармон
.pdf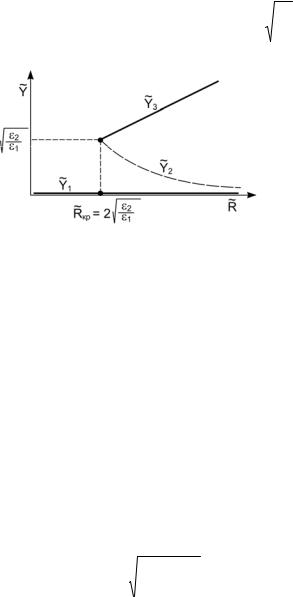
~ |
ε2 |
– здесь тоже точка |
(рис. 3.3). Очевидно, что точка Rкр = 2 |
ε1 |
|
|
|
бифуркации стационарных состояний.
Рис. 3.3. Стационарное состояние для схемы (3.23). Пояснения см. в тексте
Найдем устойчивость этих стационарных состояний путем рассмотрения релаксации малой флуктуации термодинами-
|
|
|
~ |
около стационарного решения |
~ |
|
||||||
ческого напора Y |
Yi . |
|||||||||||
Если |
~ |
~ |
|
|
|
|
|
|
|
|
|
|
Y = Yi + y , то, сохраняя линейные члены по y, полу- |
||||||||||||
чаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
~ ~2 |
~ ~ |
|
~3 |
|
~2 |
|
~ |
|
||
λy |
|
|
= ε1(R |
Yi |
+ 2R Yi |
y − Yi |
− 3 Yi |
y) − ε2 (Yi |
+ y) = |
|||
dx |
||||||||||||
|
|
|
|
|
~ |
~ |
~2 |
) − ε2 |
}y, |
|
|
|
|
|
|
|
={ε1(2R |
Yi |
+ 3 Yi |
|
|
|
|||
где λy = exp(− μoX 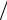 RT).
RT).
Для |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
λy dy |
= −ε2y . |
|
|
||
|
|
|
|
|
|
|
|
|
|
dx |
|
~ |
|
|
Это означает, |
что стационарное состояние |
устойчиво при |
||||||||||||
Y1 |
||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
любых значениях R . |
|
|
|
|
|
|
|
|||||||
|
~ |
|
1 |
~ |
1 |
~ |
2 |
|
ε2 |
|
|
|
||
Для |
Y2,3 |
= |
2 |
R m |
|
|
R |
|
− |
ε1 |
|
|
|
|
4 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
190

|
dy |
|
|
|
|
~ |
1 ~ |
1 ~ |
2 |
|
ε2 |
|
1 ~2 |
~ |
2 1 ~2 |
ε2 |
|||||||||||
λy |
|
={ε1[2R |
( |
|
R m |
|
|
R |
|
− |
|
|
|
) − |
3( |
|
R |
mR |
|
|
R |
− ε1 ) + |
|||||
dx |
2 |
4 |
|
|
ε1 |
4 |
4 |
||||||||||||||||||||
|
+ 4 R |
]− ε2}y ≡{[mε1 R |
|
4 R |
− ε1 ]− 2 ε2} y ≡ ϕy. |
||||||||||||||||||||||
|
|
|
1 ~2 |
|
|
|
|
|
|
|
|
~ |
1 |
|
~2 |
ε2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε2 |
|
|
|
|
|
|
||
Очевидно, что для |
~ |
|
|
|
|
~ |
|
> 2 |
значение ϕ < 0, т. е. |
||||||||||||||||||
Y3 при R |
ε1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
это стационарное состояние устойчиво. В то же время для Y2 |
|||||||||||||||||||||||||||
при |
~ |
|
|
ε2 |
выполняется |
ϕ > 0, т. е. стационарное состоя- |
|||||||||||||||||||||
R |
> 2 ε |
|
|||||||||||||||||||||||||
|
~ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ние |
неустойчиво. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
||||||||||
Таким образом, система, |
попав на ветвь решения |
||||||||||||||||||||||||||
Y2 , ока- |
|||||||||||||||||||||||||||
зывается неустойчивой и при небольшой флуктуации значе- |
|||||
~ |
переходит на ветвь |
~ |
или |
~ |
. Такое поведение сход- |
ние Y |
Y1 |
Y3 |
|||
но с поведением электронного переключателя («триггера») и поэтому его называют «триггерным».
3.5.3. Множественность устойчивых стационарных состояний при S-образных кинетических характеристиках
Аналогичным образом можно проанализировать свойства химически реакционноспособных систем, которые описываются кинетическим потенциалом D (см. выше) с S-образными характеристиками по некоторому параметру х, например сродству АrΣ брутто-реакции (рис. 3.4). Как показано в примере 3.5.2, такие системы могут обладать двумя устойчивыми стационарными состояниями и способны к скачкообразным переходам между этими состояниями при изменении управ-
ляющего параметра α вследствие скачкообразного изменения потенциальной функции dxР = dD. То есть такие системы обладают «триггерными» свойствами.
191

а |
б |
Рис. 3.4. Пример системы с S-образными характеристиками, способной к «триггерному» переключению в координатах: а – vΣ – ArΣ; б – vΣ – x. Кривые а и б построены при пробегании параметром x всей области возможных значений и соответствуют разным значениям управляющего параметра α
Пусть в такой системе имеется только одна независимая переменная х. При этом применение эволюционного критерия dxР < 0 возможно в форме полного дифференциала (3.18)
dD = dxР = vΣdArΣ,
где vΣ = dD – скорость брутто-процесса, АrΣ – его сродство, dArΣ
причем эти параметры взаимосвязаны вследствие зависимости от общей переменной х, например концентрации промежуточного реагента-интермедиата (см. § 3.2). Пусть скорости изменения параметра х в системе соответствует исходное дифференциальное уравнение общего вида
|
|
|
|
vх = dх/dt = vх(x,АrΣ,α), |
(3.25) |
где α – управляющий параметр. Стационарные |
значения |
||||
|
|
= |
|
|
|
|
x |
x(ArΣ,α) находят из уравнения |
|
||
vх(х, АrΣ, α) = 0.
Если при заданном значении управляющего параметра α стационарная скорость брутто-процесса во всей области изменения параметра x оказывается симбатной параметру АrΣ (кривая а на рис. 3.4), то значение dxР оказывается положи-
192

тельным. Это означает устойчивый характер рассматриваемого состояния для всех x .
При изменении параметра α на определенном отрезке значений x стационарное значение vΣ перестает быть симбат-
ным значению АrΣ (часть кривой б между точками х1 и х2 или А1 и А2 на рис. 3.4). Если при этом точке А1 соответствует значение х1, а точке А2 – значение х2, то на интервале x от х1 до х2 при vΣ , находящемся на «антибатном» участке кривой б,
система перестает быть устойчивой. В то же время при x < х1 для верхней части кривой б рис. 3.4 и x > х2, – для нижней стационарное состояние является устойчивым. Это означает, что при значениях сродства брутто-процесса А2 < ArΣ < A1 сис-
тема имеет множественность устойчивых стационарных состояний (в данном конкретном случае их два).
Для кривой б на рис. 3.4 в точках А1 и А2 значение производной dvΣ  dArΣ обращается в бесконечность. Следователь-
dArΣ обращается в бесконечность. Следователь-
но, при гладкой зависимости x = x(ArΣ,α) в бесконечность должна обращаться и производная dvΣ  dArΣ в точках х1 и х2.
dArΣ в точках х1 и х2.
Изменения х происходят в открытой системе. Поэтому в правой части уравнения (3.25) должны существовать члены, описывающие приток исходного реагента R из внешней среды (реакция 1)
R → Х
и отток конечного продукта превращения P во внешнюю среду (реакция 2)
Х → P.
Во многих случаях общая скорость процесса vΣ может быть определена как разность скоростей притока (v1) и оттока (v2) упомянутых реагентов:
vх = vх(x, α) = v1(x, α) – v2(x, α).
Если во внешней среде концентрация исходного реагента R и концентрация конечного продукта превращения P, выходящего из системы, остаются постоянными, то сродство химических реакций обмена с внешней средой выразится как
193

A |
r1 |
= − |
Go +RTln([R] |
x) |
|
|
|
|
r 1 |
|
|
|
|
для поступления исходного реагента со скоростью v1(x,α) и |
|
|||||
Ar2 = − |
rGo2 +RTln(x |
[P]) |
|
|
||
для оттока продукта реакции со скоростью v2(x,α). Здесь |
r |
Go |
||||
|
|
|
|
|
1 |
|
иrGo2 – стандартные значения потенциала Гиббса для реак-
ций 1 и 2. При этом
dAr1 |
= −RT dx |
; |
dAr2 |
= RT dx . |
|
x |
|
|
x |
Тогда общее изменение кинетического потенциала dD примет вид
dD = v1(x,α) dAr1 – v2(x,α) dAr2,
с учетом соотношений для dAi
dD = −RTv1(x,α) dxx +RTv2 (x,α)dxx = −RTvx (x,α)dxx ,
dD / dx = –RTvΣ(x,α) / x.
Найдем значение потенциала D в стационарных точках, расположенных на разных ветвях S-образной кривой стационарных состояний. При этом вторая производная d2D / dx2 в
некоторой стационарной точке |
|
= |
|
|
|
|
|||||
x |
x(α) определяется выра- |
||||||||||
жением |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
dvx (x,α) |
2 |
|
|
||||
d D / dx |
|
= –RT [ |
|
|
|
/x − vx (x,α) / x ] |
|
(α) . (3.26) |
|||
|
dx |
|
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Так как в точке |
|
|
в связи |
с |
условием стационарности |
||||||
x(α) |
|||||||||||
vx (x,α) = 0 , а х(α) > 0 по смыслу задачи, то знак второй производной d2D / dx2 противоположен знаку производной dx(x,α) / dx в стационарной точке x(α) .
194

Согласно эволюционному термодинамическому критерию (3.19), в стационарном состоянии потенциальная функция D(x) принимает минимальное значение, при этом в устойчивом стационарном состоянии ее вторая производная положительна. Поэтому, если знак первой производной правой части (3.26) в стационарной точке отрицателен, то согласно указанному математическому критерию это означает устойчивость стационарного состояния. Такая устойчивость имеет место для любой точки кривой а, а также для верхней (при х < х2) и нижней (при х > х1) ветвей кривой б на рис. 3.4. В неустойчивых стационарных состояниях потенциал D в точке x(α) принимает минимальное значение, но его вторая произ-
водная отрицательна, так как знак первой производной dvх(x,α) / dx в этой точке положителен. Этому соответствует центральная часть (x1 < x < x2) кривой б на рис. 3.4.
Во всех точках верхней и нижней ветвей S-образной кривой б значения производных правых частей соответствующих дифференциальных уравнений отрицательны, а для промежуточного участка положительны. Таким образом, термодинамические критерии устойчивости стационарного состояния совпадают с соответствующими математическими признака-
ми. При этом значению управляющего параметра α, для которого характерна кривая а на рис. 3.4, отвечает только одно
устойчивое стационарное состояние, а значению α, описывающему кривую б, – два (верхняя I и нижняя II ветви кривой б). Очевидно, что при этом можно найти и бифуркационное
значение параметра α*, при котором трансформация вида S-образной кривой v(A,α) из вида а в вид б впервые даст зна-
чение dvΣ(x,α*) dArΣ = ∞ или dvx (x,α*)
dArΣ = ∞ или dvx (x,α*) dx = ∞ .
dx = ∞ .
Качественный вид типичной фазовой диаграммы стационарного значения некоторого внутреннего параметра «триггерной» системы приведен на рис. 3.5.
195

Рис. 3.5. Типичная фазовая диаграмма стационарного значения некоторого внутреннего параметра «триггерной» системы с двумя устойчивыми стационарными состояниями
(ср. с рис. 3.2)
С термодинамической точки зрения значение функционала диссипации энергии Р (или положительно определенной функции Ляпунова Φ) в устойчивых стационарных точках имеет локальные минимумы, а скачкообразные самопроизвольные переходы в системе между устойчивыми стационарными состояниями возможны в том случае, когда два состояния обладают одинаковыми «входными» параметрами, например обеспечивающим процесс и задаваемым «извне» общим сродством АrΣ. Можно считать поэтому, что эти переходы связаны с преодолением некоторого «потенциального» барьера, как схематически показано на рис. 3.8.
3.5.4. Устойчивость кинетических схем по Ляпунову
Рассмотрим алгоритм анализа кинетических систем на устойчивость в общем случае, когда число внутренних переменных более одного. Пусть система включает два «внутренних» параметра y и z, эволюция которых описывается системой дифференциальных уравнений:
|
|
|
|
|
|
|
|
|
|
dy dt = P(y |
+ y; z + z,α), . |
(3.27) |
|||||||
|
|
+ y; |
|
+ z,α). |
|
||||
dz dt = Q(y |
z |
|
|||||||
Здесь y и z – исходное стационарное положение системы, а
β – некоторый внешний «управляющий» параметр (напри-
мер, сродство, температура, общее давление и т. п.), характеризующий удаленность точки ( y, z ) от положения равновесия.
Эволюцию данной модели («фазовые траектории») вблизи стационарного состояния при выводе системы из этого со-
196

стояния можно найти, линеаризуя уравнение (3.27) по малым параметрам y и z в систему характеристических уравнений
dy / dt = ay + bz, dz / dt = cy + dz,
где |
a = |
∂P |
|
|
|
|
, b = |
∂P |
|
|
|
|
, c = |
∂Q |
|
|
|
|
|
, d = |
∂Q |
|
|
|
|
|
. Управляющий |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y,z |
|
|
y,z |
||||||||||||||||
|
|
|
y,z |
|
|
y,z |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
параметр β влияет на значение параметров а, b, с и d и может менять их.
Общее решение обсуждаемой системы уравнений можно записать в виде
y |
y1 |
|
λ t |
y2 |
|
λ |
t |
|
|
|
|
|
|
1 |
|
|
2 |
|
. |
|
|
= |
e |
|
+ |
e |
|
|
|
z |
z1 |
|
|
z2 |
|
|
|
|
|
Здесь (yi,zi) – собственные векторы для данной системы уравнений, а λ1 и λ2 являются характеристическими числами «векового» уравнения
|
|
|
a − λ |
b |
|
= 0 . |
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
c |
|
d − λ |
|
|
|
|
|
|
Очевидно, что |
|
|
|
|
|
|
|
||||
λ1,2 = |
1 |
[(a + d) ± (a + d)2 |
− 4(ad − bc)]≡ |
1 |
[− γ ± γ2 |
− 4 ], |
|||||
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
где γ = –(а + d), = ad – bc.
Устойчивые решения характеризуются возвращением решения в исходную стационарную точку с течением времени. Тип устойчивости решения зависит от величины характеристических чисел и рассмотрен на диаграмме (рис. 3.6), пред-
ставленной в координатах γ, . На диаграмме помечены пять областей I–V, которые характеризуются разными типами устойчивости решения.
197

Рис. 3.6. Диаграмма типов устойчивости особых точек системы линейных дифференциальных уравнений dy/dt = ay + bz; dz/dt = cy + dz (по М. Ф. Ляпунову)
Пусть λr – действительная, а λi – мнимая части характе-
ристического числа. Устойчивые точки характеризуются отрицательной действительной частью чисел λ (λr < 0) и распо-
лагаются в областях I и II (γ > 0, |
> 0), которые разделены |
параболой γ2 / 4 = . Для точек |
в области I, кроме того, |
γ2 – 4 > 0 и, следовательно, λi = 0. Поэтому при небольшом начальном отклонении от исходной точки система неизбежно вернется (проэволюционирует) в эту же точку по кривым, схематически помеченным на рис. 3.6. По определению, предложенному М. Ф. Ляпуновым, область I соответствует ус-
тойчивым узлам.
В области II γ2/4 < и поэтому λi ≠ 0. Эта область соответствует устойчивым фокусам, так как эволюция системы в исходную точку описывается спиральной кривой.
Неустойчивые фокусы и узлы расположены соответст-
венно в областях III и IV (λr > 0) и также разделены кривой γ2 / 4 = . На оси γ = 0 расположены точки типа центр, для ко-
торых λr = 0, λi ≠ 0 и λ1,2 = ±iλ.
198
Область V соответствует особым неустойчивым точкам ти-
па седло. Здесь λi = 0, а λr имеют разные знаки (λ1 > 0, λ2 < 0). Положение точки устойчивого термодинамического равновесия системы всегда находится в области I. Изменение параметра α может изменить величины коэффициентов характеристического уравнения, описывающего поведение системы после ее вывода из равновесия, и, следовательно, вели-
чин λ1 и λ2 (см. рис. 3.6). Такое изменение может привести не только к изменению координат особой точки «устойчивый узел», но и к изменению самого типа устойчивости ста-
ционарного состояния, если при этом система покинет область I устойчивых узлов.
Отметим, что, как следует из приведенного выше, в качестве необходимого (но далеко не достаточного) условия для возникновения осцилляций в эволюции концентрации интермедиатов (т. е. мнимой части в показателе экспоненты) кроме необходимых условий для возникновения неустойчивости стационарного состояния необходимо также наличие не ме-
нее чем двух интермедиатов.
Сходный анализ можно провести и для систем с более чем двумя независимыми переменными. При этом используется аналогичная классификация устойчивости точек фазовой диаграммы исходя из значения характеристических решений соответствующего векового уравнения. Положения устойчивых и «притягивающих» к себе состояний динамической системы в последнее время нередко принято называть «аттракторами».
Переходы между областями I–V устойчивости особых точек можно соотнести с изменением значения управляющего пара-
метра α. На типичной диаграмме рис. 3.7 по оси ординат отложены значения координат стационарной точки х, а по оси абс-
цисс – значения управляющего параметра α, отражающего степень удаленности системы от исходного равновесия.
199
