Учебники / Лекции по термодинамике неравновесных систем. Пармон

Здесь {Xi}, {Yj} и {Zm} имеют то же значение, что и ранее. Соответствующая функция Ляпунова записывается в виде

Очевидно, что сходным образом можно найти функции Ляпунова и для иных брутто-реакций с линейными по интермедиатам превращениям и произвольным числом исходных реагентов Ai и конечных продуктов Pj.

Существенно, что во всех описанных случаях функционалы Φ являются положительно определенными, что означает устойчивость стационарного состояния для соответствующих брутто-процессов. Для сильнонелинейных кинетических схем условия устойчивости надо рассматривать специально. Так, несложно показать, что положительная определенность функционала Φ действительно является необходимой для устойчивости стационарного состояния соответствующего химического процесса (естественно, в ситуации, если такие функционалы существуют).

Пример 5

Рассмотрим брутто-реакцию

R P,

которая осуществляется через совокупность промежуточных превращений, имеющих автокаталитические стадии:

R {Xi}, R + Xi 2Xi,

{Xj} P.

171

Здесь, как и ранее, {Xi} обозначает произвольную совокупность мономолекулярных превращений интермедиатов Xi

(i = 1, …, k).

Для данной кинетической схемы функция, производная которой принимает нулевое значение в стационарном состоя-

нии относительно «внутренних» переменных ~ , может быть nXi

выражена в виде

Действительно, в стационарном состоянии по отношению к интермедиатам Xi мы имеем

Однако выражение (3.16) не всегда положительно. Это означает, что стационарное состояние рассматриваемой бруттореакции является уже не обязательно устойчивым. На самом деле, автокаталитические реакции при определенных соотношениях концентраций реагентов являются ярким примером процессов с неустойчивостью стационарного состояния.

3.3.3. Примеры анализа устойчивости стационарного состояния брутто-процессов, нелинейных относительно интермедиатов, кинетическими методами

Пример 1

Рассмотрим устойчивость простой нелинейной брутто-

реакции (1.27)–(1.28).

Рассмотрим малое отклонение δ от стационарного значе-

ния ~ ≡ ~ :

Y

Y

172

~ ≡ ~ +

Y Y y .

При этом

[Y] = [Y] + A y ,

где [Y] – стационарное значение концентрации интермедиата

Y, а А – некоторый положительный коэффициент, не зависящий от y.

Тогда, сохраняя члены, линейно зависящие от малого отклонения y, получаем

Таким образом, эволюция y во времени передается функ-

т. е. всегда экспоненциально убывает со временем.

~

Следовательно, стационарное решение Y для рассматриваемой схемы всегда является устойчивым.

Как видно будет далее, для эволюции сложных систем большое значение имеет устойчивость стационарного состояния интермедиатов при постоянстве внешних параметров. Особенно большое значение это имеет для схем превращений, нелинейных относительно интермедиатов.

Пример 2

Рассмотрим брутто-реакцию

R P,

которая осуществляется по автокаталитической схеме с од-

ним интермедиатом-автокатализатором: R + X ε1 2 X

173

X ε2 P.

Найдем условия возникновения неустойчивости стационарного состояния.

Кинетика изменения концентрации интермедиата Х описывается уравнением

Найдем приращение диссипации энергии при возникновении малой флуктуации в концентрации (напоре) интермедиата:

~ = ~ +

X X x ,

= ~ − ~ Ar1 RT(lnR ln X) ,

174

Таким образом, неустойчивость возникает при

ε2 − α2 +β > 0 , ε1

или, что то же,

Можно сделать чисто кинетическое рассмотрение наличия устойчивости путем рассмотрения кинетики релаксации флуктуации х:

dxdt ~ ε1 R~x − 2X~x − ε2x = ε1 R~ − 2X~ − ε2 x .

Очевидно, что неустойчивость возникает при

175

что полностью совпадает с термодинамическим рассмотрением.

Пример 3

Рассмотрим устойчивость стационарного состояния для брутто-процесса

R → P,

осуществляющегося по автокаталитической схеме Лотки– Вольтера с двумя интермедиатами Х и Y:

d[Y] = k2 [X] [Y] −k3 [Y] . dt

Единственным ненулевыми стационарными решениями для схемы (3.17) являются

[X]o = k3 / k2, [Y]o = k1A / k2.

Пусть в момент пребывания системы в стационарном состоянии (Xo,Yo) возникла флуктуация концентраций сразу обоих интермедиатов:

[Х] = [Х]о + х,

[Y]= [Y]о + y.

Вслучае малости х и y кинетика развития этой флуктуации

вокруг точки ([X]o,[Y]o) описывается системой дифференциальных уравнений:

dxdt = (k1[A] −k2 [Y]o )x −k2 [X]o y = −k3 y ,

176

dydt = k2 [Y]o x + (k2 [X]o −k3 )y = k3 [Y]o x .

Для нахождения решения этой системы дифференциальных уравнений надо решить вековое уравнение

Таким образом, состояние системы после возникновения флуктуации из единственного ненулевого стационарного состояния

Поскольку λ1 и λ2 – мнимые величины, это означает, что концентрации интермедиатов Х и Y осциллируют вокруг стацио-

177

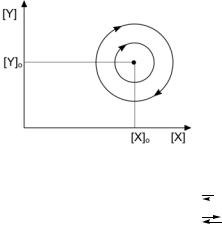
Это соответствует ситуации «центр» по Ляпунову (см. рис. 3.1 и подразд. 3.5.4).

Рис. 3.1. Фазовая диаграмма, описывающая незатухающие периодические решения вокруг стационарного состояния для схемы Лотки– Вольтера

Эволюцию рассматриваемой системы, но со схемой пре-

вращений, в которой все реакции обратимы

ε1

А + Х ε 2 Х,

Х+ Y ε3 2 2 Y, Y Р,

проще анализировать с использованием термодинамической форме записи кинетических уравнений

Стационарное решение находится из уравнений

и, следовательно,

178

где коэффициенты λх и λy служат для перевода значений напоров в концентрации.

Отсюда

Для описания эволюции флуктуаций надо найти показатели экспонент в решении этой системы уравнений:

~ ~

где X и Y – значения в стационарном состоянии.

При a priori заданной кинетической необратимости обеих нелинейных стадий схемы превращений стационарные значения

179

Отсюда в точке ненулевого стационарного состояния

Таким образом

что соответствует решению, найденному традиционными кинетическими методами.

§ 3.4. Критерии эволюции в нелинейной термодинамике. Универсальный критерий эволюции Гленсдорфа–Пригожина

В открытых сильнонеравновесных системах линейные соотношения Онзагера не выполняются. Универсальным критерием эволюции таких систем является обобщение принципа минимальной скорости производства энтропии на нелинейные процессы. Ниже рассмотрено содержание этого критерия для систем как однородных, так и имеющих пространственную неоднородность.

3.4.1. Универсальный критерий эволюции для пространственно однородной системы

Выше показано, что в области линейной неравновесной термодинамики (т. е. действия линейных соотношений Онзагера) стремление системы к стационарному состоянию характеризуется монотонным уменьшением скорости производства энтропии (скорости диссипации энергии) в результате внут-

ренних необратимых процессов: dР ≤ 0 и ddtP ≤ 0 .

Вдали от положения термодинамического равновесия найти общий количественный критерий направления движения системы к стационарному состоянию в общем случае обычно

180