
- •1. Особенности микроволнового диапазона электромагнитных колебаний. Применение микроволновых приборов:
- •3. Основные уравнения микроволновой электроники – уравнения электродинамики и уравнения движения заряженных частиц в вакууме и твердом теле.
- •В вакууме:
- •В твердом теле:
- •5. Наведённый ток. Теорема Шокли-Рамо. Упрощённое выражение для мощности взаимодействия. Удельная мощность потока с переменным полем.
- •6. Наведённый ток. Время и угол пролёта носителей заряда в пространстве взаимодействия, коэффициент взаимодействия, электронная нагрузка.
- •7. Анализ особенностей движения носителей заряда в вакууме и твердом теле. Сравнение типовых значений скорости носителей и плотности зарядов. Направления совершенствования приборов.
- •9. Понятия о колебательных и волновых явлениях в потоках заряженных частиц (пзч). Плазменные колебания в твердом теле.
- •10. Приборы с квазистатическим управлением. Причины ограничения частотного диапазона приборов данного класса. Характерные конструкции.
- •11. Приборы с динамическим управлением о-типа с кратковременным взаимодействием: клистроны. Скоростная модуляция в высокочастотном зазоре. Коэффициент взаимодействия, электронная нагрузка.
- •Клистроны
- •Принцип действия и схема клистрона:
- •Скоростная модуляция в высокочастотном зазоре.
- •Коэффициент взаимодействия, электронная нагрузка.
- •12. Приборы с динамическим управлением о-типа: лампы бегущей и обратной волны. Скоростная модуляция в замедляющей системе, сопротивление связи.
- •13. Скоростная модуляция в высокочастотном зазоре резонатора и замедляющей системе. Коэффициент взаимодействия, сопротивление связи.
- •Конструкции и параметры приборов.
- •15. Приборы со скрещенными полями (м-типа): - магнетроны, амплитроны и митроны. Принцип действия, коэффициент полезного действия. Основные конструктивные разновидности. Сравнение с приборами о-типа
- •Работа магнетрона в статическом режиме, т.Е. При отсутствии вч поля. (Принцип действия)
- •Амплитрон (платинотрон)
- •16. Гирорезонансные приборы. Гиротрон – источник мощного излучения в мм диапазоне. Принцип действия. Типовые конструкции. Параметры.
- •17. Релятивистские приборы. Лазеры на свободных электронах: принцип действия характеристики.
- •18. Классификация диодов с положительным динамическим сопротивлением. Функциональная роль (на примере типового приемо-передатчика). Омические и барьерные контакты в структурах диодов.
- •20. Диоды с положительным динамическим сопротивлением: смесительные диоды: конструкция, вах, вч параметры, эквивалентная схема. Особенности схемотехнического применения. Принцип действия смесителя.
- •24. Динамическое сопротивление полупроводникового образца. Слоистые структуры. Способы получения отрицательного динамического сопротивления.
- •27. Способы повышения предельной частоты и мощности транзистора. Сравнение материалов для изготовления транзисторов: кремний, арсенид галлия, карбид кремния, нитрид галлия, фосфид индия, алмаз.
- •28. Схемотехнические аспекты применения транзисторов в микроволновом диапазоне. Малошумящий усилитель.
- •29. Природа шумов в птш. Шумовая схема полевого транзистора. Анализ экспериментальных шумовых характеристик и их интерпретация.
- •30. Моделирование транзисторов: локально-полевая модель Шокли, модель двух областей, температурные модели.
- •32. Способы повышения предельной частоты и мощности микроволнового биполярного транзистора. Выбор материалов для изготовления транзисторов.
- •33. Схемотехнические аспекты применения биполярных транзисторов в микроволновом диапазоне. Усилитель мощности.
- •34. Источники шумов в элементах микроволновых цепей. Спектральные и корреляционные характеристики. Математическое описание мощности шума: формула Найквиста, формула Ван-дер-Зила.
- •35. Описание шумов двух и четырехполюсника. Эквивалентное шумовое представление диодов, транзисторов и пассивных элементов. Расчет коэффициента шума каскадного соединения.
- •36. Способы снижения коэффициента шума приборов. Сравнительная характеристика приборов по шумовым параметрам.
В вакууме:
Если рассматриваются частицы только
одного сорта, для них вводят одночастичную
функцию распределения f(r, p,
t). Эта функция определяет число
частиц, находящихся в элементе шестимерного
фазового пространства dn(t) = f(r,
p, t)dVdP в момент времени t.
Элемент фазового пространства определяется
объемом пространства dV(r),
расположенным вокруг точки с радиус
вектором r и объемом пространства
импульсов dP(p), содержащего
частицы со импульсами, близкими к
импульсу p. Очевидно, что интеграл
от функции распределения по всем
возможным импульсам должен быть равен
числу частиц в единице объема, т. е. их
концентрации:
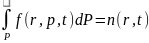

В качестве примера приведем так называемую максвелловскую функцию распределения, которой в ряде практически важных случаев соответствует распределение электронов по скоростям в электронном потоке вакуумных приборов с учетом теплового разброса скоростей:
!
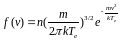 !
!
где Te — так называемая электронная температура, характеризующая среднюю энергию теплового движения электронов.
Сформулируем уравнение движения (переноса) для ансамбля частиц одного сорта в вакууме. Для этого используем теорему Лиувилля, которая утверждает, что функция распределения остается постоянной вдоль любой траектории в фазовом пространстве, т. е.
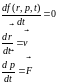

где индексами r и p отмечены операторы, действующие на координаты и проекции импульса соответственно.
Если к полю сил F добавить силу воздействия самосогласованного поля, зависящего от функции распределения, получим уравнение Власова, описывающее движение частиц в поле, равном сумме внешнего поля и поля, создаваемого самими частицами. Такой подход используется в вакуумных приборах для анализа движения частиц при наличии теплового разброса скоростей в электронном потоке.
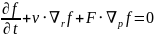 – вакуума (уравнение Власова)
– вакуума (уравнение Власова)
В твердом теле:
В отличие от движения частиц в вакууме, при анализе процессов переноса в твердом теле необходимо учитывать процессы рассеяния, рекомбинации и генерации частиц. Надо учитывать столкновительный член, который есть в кинетическом уравнении Больцмана:
!
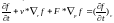 !
!
Проинтегрировав его по пространству импульсов, получим закон сохранения числа частиц:
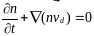
(отсылка на вопрос №4)
Законы движения заряженных частиц в твердом теле существенно отличаются от законов их движения в вакууме. Эти отличия обусловлены следующими факторами:
свободные ЗЧ в твердом теле движутся в периодическом поле кристаллической решетки. Влияние этого поля в первом приближении можно учесть, введя эффективную массу частицы m*, отличную от действительной ее массы;
при температуре, большей абсолютного нуля, атомы кристаллической решетки совершают колебания, что приводит к столкновениям со свободными ЗЧ и приобретению последними хаотических тепловых скоростей. При столкновении величина и направление скорости частицы меняются случайным образом. Эти процессы называют процессами рассеяния;
скорости, приобретаемые ЗЧ под действием электрического поля, обычно много меньше или сравнимы с тепловыми скоростями.
Движение носителей заряда в твердотельной или газовой плазме сопровождается большим количеством актов столкновений (рассеяния). Физическая природа актов рассеяния очень разнообразна. Это рассеяние на заряженных и нейтральных компонентах среды, рассеяние на фононах, на дислокациях кристаллической решетки, межэлектронное рассеяние и т. п. Стохастический характер этих процессов, сильная зависимость от напряженности поля, энергии частицы, температуры, концентрации приводит к необходимости использовать кинетическое уравнение Больцмана для описания процессов токопереноса. При этом важную роль играет правильная аппроксимация столкновительного члена в этом уравнении. Часто используют приближение времени релаксации, полагая, что скорость изменения во времени данной физической величины пропорциональна разности между ее текущим и некоторым равновесным значениями. Математически это представляется дифференциальным уравнением вида:
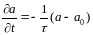
где a(t) — любая величина, характеризующая плазму; a0 — ее равновесное значение; Ʈ — коэффициент, называемый постоянной релаксации данной величины.
В процессе движения зарядов в полупроводниках происходит релаксационные процессы, связанные с генерацией и рекомбинацией зарядов. Эти процессы характеризуются временем жизни носителей: электронов — Ʈn, дырок— Ʈp. Для того чтобы приборы работали в микроволновом диапазоне, необходимо иметь материал с временем жизни носителей заряда много боольшим, чем период микроволновых колебаний T. Для электронов это условие запишется в виде неравенства Ʈn >> T
Уравнение Ньютона (вакуум) (Для одиночного заряда или ансамбля зарядов с одинаковой скоростью v) Невозможно использовать т.к. количество частиц очень большое.
Кинетическое уравнение Больцмана (Власова) Для ансамбля зарядов с распределением по скоростям и импульсам и по времени f(r,p,t)
 – для плазмы твердого тела
– для плазмы твердого тела
Кинетическое уравнение Больцмана для ансамбля зарядов с распределением по скоростям и импульсам и по времени f(r,p,t)
n(r,t) – концентрация частиц в данный момент времени в данной точке пространства (r-радиус вектор)
Найдём среднюю скорость и ток:
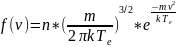 - Распределение Максвелла
- Распределение Максвелла
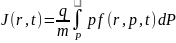
При субатомных размерах мы пользуемся уравнением Шрёдингера
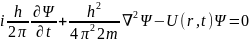
U(r,t) – внешняя по отношению к частице потенциальная энергия поля в точке r.
4. Законы сохранения: числа частиц, импульса и энергии. Характерные пространственные и временные интервалы: время релаксации импульса и энергии, время максвелловской релаксации, плазменная частота и длина Дебая, время жизни и диффузионная длина.
Законы сохранения:
(1)
Используя приближение времени релаксации, полагают, что скорость изменения во времени данной физической величины пропорциональна разности между ее текущим и некоторым равновесным значениями.
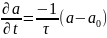
где a(t) — любая величина, характеризующая плазму, a0 — ее равновесное значение, τ — коэффициент, называемый постоянной релаксации данной величины.
Числа частиц:
Использование приближения времени релаксации и интегрирования уравнения (1) по пространству скоростей дает уравнение сохранения числа частиц:
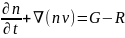 (2)
(2)
где n — концентрация заряженных частиц, vd — скорость их дрейфа, G — скорость генерации частиц, R — скорость рекомбинации.
Потока импульса:
Умножение уравнения (1) на v с последующим интегрированием по пространству скоростей дает уравнение переноса или уравнение сохранения потока импульса:
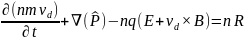 (3)
(3)
Лучше записать так :
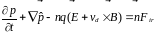
И пояснить, что:
p = mnvd — удельный импульс;
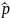 = рvd
— тензор (диада) потока импульса;
= рvd
— тензор (диада) потока импульса;
∇⋅ — пространственная расходимость потока импульса;
nFir— эффективная сила внутреннего трения, отражающая изменение импульса за счет актов рассеяния.
Тензор давления (или напряжений)
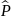 представляет собой тензор второго
ранга (диаду) и определяется следующим
образом. Если dS - ориентированный
элемент площади поверхности, то
* dS определяет поверхностную
силу, действующую со стороны частиц,
находящихся в направлении ориентации
вектора dS, на частицы, расположенные
с противоположной стороны элемента
поверхности.
представляет собой тензор второго
ранга (диаду) и определяется следующим
образом. Если dS - ориентированный
элемент площади поверхности, то
* dS определяет поверхностную
силу, действующую со стороны частиц,
находящихся в направлении ориентации
вектора dS, на частицы, расположенные
с противоположной стороны элемента
поверхности.
Энергии:
Умножение уравнения (1) на v2 и интегрирование по всему пространству скоростей дает уравнение сохранения энергии:
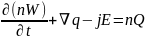 (4)
(4)
где
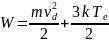 – полная энергия частицы,
– полная энергия частицы,
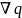 – пространственная расходимость
потока энергии
– пространственная расходимость
потока энергии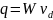 , jE - джоулево тепло, Q - изменение d
энергии за счет процессов рассеяния.
, jE - джоулево тепло, Q - изменение d
энергии за счет процессов рассеяния.
Уравнения (2)-(4) можно привести к более
простому виду, если использовать
приближение времени релаксации
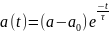
 (5)
(5)
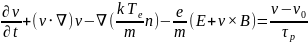 (6)
(6)
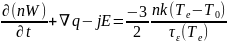 (7)
(7)
где τn - время релаксации зарядов (время жизни), p - время релаксации n импульса частицы, ε - время релаксации энергии частицы.
Время релаксации импульса и энергии:
Время релаксации τp импульса mv характеризует скорость изменения (уменьшения) импульса при снятии возбуждения. Согласно приближению времени релаксации запишем:
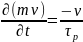
Для одномерного случая:
v(t)=v(0)exp(-t/τ)
Величина τp имеет смысл среднего времени свободного пробега. Если эту величину умножить на среднеквадратичную тепловую скорость vT, то T получим среднюю длину свободного пробега частицы lp:

Релаксация энергии частицы происходит с другим характерным временем, т.к. для потери избыточной энергии частице необходимо совершить большое количество актов рассеяния.
По аналогии с длиной свободного пробега введем в рассмотрение некое расстояние, на котором происходит релаксация энергии. Назовем это расстояние длиной «остывания» - lε . В случае подачи электрического поля, логичнее назвать эту величину длиной «разогрева». Оценим эту длину следующим образом:
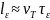
Время релаксации заряда (максвеловское время релоксации):
Работа любого электронного прибора связана с созданием избытка зарядов в некотором пространстве, по сравнению с равновесным состоянием. Естественно, за счет сил электрического взаимодействия будет происходить изменение такой зарядовой неоднородности. Найти характерное время релаксации заряда можно с помощью уравнений Максвелла. Часто это время и называют максвелловским временем релаксации заряда.
Рассмотрим некоторую среду с проводимостью σ и диэлектрической проницаемостью ε, в которую помещён заряд объёмной плотность ρ.
Определим характер изменения во времени этого заряда. Используя оператор дивергенции от правой и левой части 1-го уравнения Максвелла, учитывая выражение div(rot(H))=0 и уравнение Пуассона, получим уравнение для нахождения ρ.
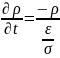 =>
=>
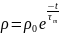 – релаксация заряда,
– релаксация заряда,
Где
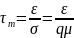 – время максвеловской релаксации,
ρ0 – заряд в момент времени t=0.
– время максвеловской релаксации,
ρ0 – заряд в момент времени t=0.
Период плазменных колебаний, длина Дебая:
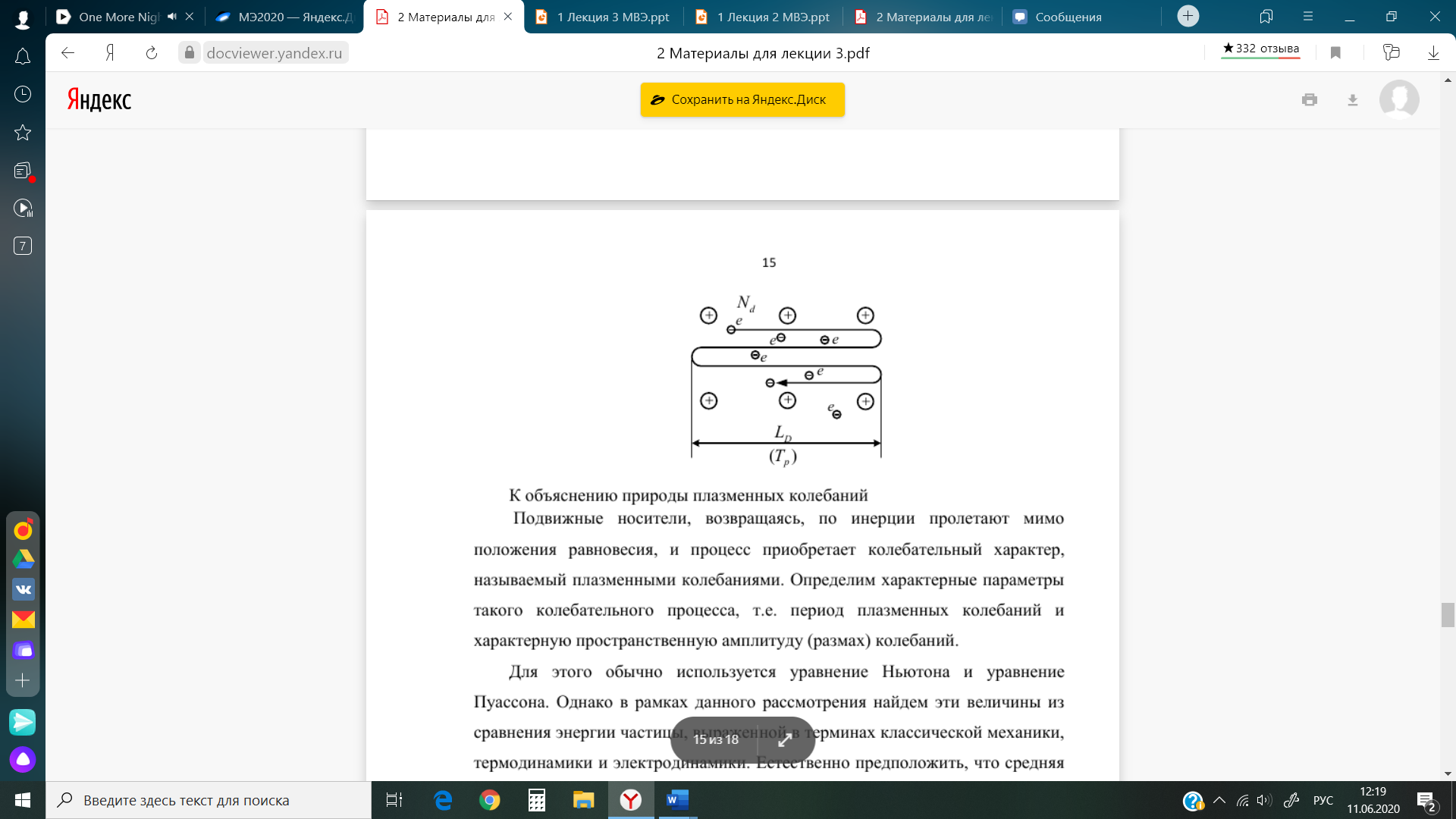
Подвижные носители, возвращаясь, по инерции пролетают мимо положения равновесия, и процесс приобретает колебательный характер, называемый плазменными колебаниями. Определим характерны параметры такого колебательного процесса, т.е. период плазменных колебаний и характерную пространственную амплитуду (размах) колебаний.
Средняя энергия частицы, определенная по термодинамическим соотношениям должна быть равна кинетической энергии частицы и энергии, определенной по законам электродинамики: Wтерм= Wмех= Wэд
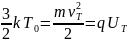
где vT-среднеквадратичная тепловая скорость, UT-характерный тепловой потенциал. Определим пространственное распределение этого теплового потенциала при разделении доноров и электронов на некоторое расстояние x , используя уравнение Пуассона для одномерного случая:
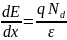
Считая уровень легирования не меняющимся
по координате (Nd=const),
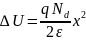 =>
=>
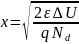
Максимальное расстояние, на которое сместиться электрон обозначим LD (длина Дебая). Возникшую за счёт разделения зарядов разность потенциалов ΔU на этом расстоянии обозначим UT. Тогда:
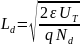
Заменим UT через энергию:
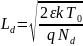
Определим период плазменных колебаний Tp
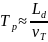 =>
=>
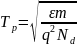
Плазменная частота
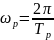 :
:

Время жизни неосновных носителей, диффузионная длина:
В процессе движения зарядов в
полупроводниках происходят релаксационные
процессы, связанные с генерацией и
рекомбинацией зарядов. Для того чтобы
приборы работали в микроволновом
диапазоне, необходимо выполнить условие
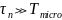 во временной области и
во временной области и
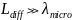 в пространственной.
в пространственной.
Практические измерения времени жизни
носителей заряда в полупроводниках
показали величину
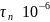 .
Пространственный интервал, связанный
с этой величиной, называется диффузионной
длиной Ldiff и рассчитывается с
помощью следующего соотношения:
.
Пространственный интервал, связанный
с этой величиной, называется диффузионной
длиной Ldiff и рассчитывается с
помощью следующего соотношения:
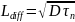
где D -коэффициент диффузии.
Подстановка реальных значений для τn и D показывает, что условия в пространственной Ldiff >>λmicro и во временной области τn>>Tmicro выполняются.
