
Кинематика
.pdfФедеральное агентство по образованию Федеральное государственное образовательное учреждение
высшего профессионального образования
Сибирский федеральный университет
Т. А. Валькова В.В. Вальков Н. В. Еркаев А.А. Шаронов
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Курс лекций
Утверждено Редакционно-издательским советом в качестве учебного пособия
Под общей редакцией Т. А. Вальковой
Красноярск 2007
УДК 531(07)
В
В Теоретическая механика. Курс лекций: Учеб. пособие / Т. А. Валькова, В. В. Вальков, Н. В. Еркаев, А. А. Шаронов; Под общ. ред. Т. А. Вальковой. − Красноярск: ИПЦ ПИ СФУ, 2007. − 226 с.
ISBN
Освещен теоретический материал по всем разделам теоретической механики: кинематике, статике, динамике и основам аналитической механики.
Предназначены для студентов направлений подготовки бакалавров 150400.62 Технологические машины и оборудование, 150600.62 Материаловедение и технология новых материалов, 150900.62 Технология, оборудование и автоматизация машиностроительных производств, 190100.62 Наземные транспортные системы, 190500.62 Эксплуатация транспортных средств.
|
УДК 531(07) |
ISBN |
© СФУ, 2007 |
|
© Валькова Т. А., Вальков В. В., |
|
Еркаев Н. В., Шаронов А. А. |
|
2007 |
Технический редактор
Гигиенический сертификат № 24.49.04.953.П.000338.05.01 от 25.05.2001.
Подп. в печать |
Формат 60 84/16. Бумагатип. №1. Офсетнаяпечать. |
||
Усл. печ. л. |
. Уч.-изд. л. . Тираж |
экз. Заказ |
С |
Отпечатано в ИПЦ ПИ СФУ 660074, Красноярск, ул. Киренского, 28
ОГЛАВЛЕНИЕ |
|
Модуль 1. Кинематика |
6 |
Лекция 1. Кинематика |
6 |
Кинематика точки |
7 |
Векторный способ |
7 |
Координатный способ |
8 |
Естественный способ |
10 |
Лекция 2. Кинематика твердого тела |
14 |
Поступательное движение твердого тела |
14 |
Вращательное движение твердого тела вокруг |
|
неподвижной оси. |
15 |
Угловая скорость и угловое ускорение |
15 |
Скорости и ускорения точек вращающегося тела |
19 |
Выражения скорости точки, касательного и нормального |
|
ускорений в виде векторных произведений |
20 |
Лекция 3. Плоскопараллельное (плоское) движение твердого тела |
22 |
Скорости точек плоской фигуры |
23 |
Теорема о проекциях скоростей двух точек плоской фигуры |
25 |
Мгновенный центр скоростей |
25 |
Ускорения точек плоской фигуры |
28 |
Лекция 4. Сложное (составное) движение точки |
30 |
Теорема о сложении скоростей |
30 |
Теорема Кориолиса о сложении ускорений |
33 |
Модуль 2. Статика |
36 |
Лекция 5. Введение в статику |
|
36 |
|
Аксиомы статики |
36 |
Связи и их реакции |
38 |
Проекция силы на ось и на плоскость |
40 |
Аналитический способ задания силы |
42 |
Геометрический способ сложения сил |
42 |
Разложение силы |
43 |
Аналитический способ сложения сил |
43 |
Равновесие системы сходящихся сил |
44 |
Теорема о трех силах |
45 |
Лекция 6. Момент силы относительно центра |
45 |
Пара сил. Момент пары |
47 |
Теорема о параллельном переносе силы |
49 |
Теорема Пуансо |
50 |
Условия равновесия |
51 |
Теорема Вариньона |
52 |
Лекция 7. Произвольная плоская система сил |
53 |
Условия равновесия плоской системы сил |
54 |
Распределенные силы |
56 |
Равновесие системы тел |
57 |
Трение сцепления и скольжения |
59 |
Трение качения |
62 |
Лекция 8. Пространственная система сил |
65 |
Момент силы относительно оси |
65 |
Вычисление главного вектора и главного момента |
|
пространственной системы сил |
67 |
Частные случаи приведения пространственной системы сил |
68 |
Уравнения равновесия для пространственной системы сил |
71 |
Лекция 9. Центр параллельных сил |
73 |
Центр тяжести твердого тела |
76 |
Модуль 3. Динамика |
81 |
Лекция 10. Динамика. Динамика материальной точки |
81 |
Законы классической механики |
81 |
Дифференциальные уравнения движения |
|
материальной точки |
|
83 |
|
Две задачи динамики |
84 |
Лекция 11. Прямолинейные колебания точки |
87 |
Свободные колебания точки |
|
88 |
|
Затухающие колебания точки |
|
95 |
|
Лекция 12. Вынужденные колебания точки |
|
при отсутствии сопротивления |
99 |
Вынужденные колебания точки |
|
при вязком сопротивления |
|
102 |
|
Лекция 13 .Динамика относительного движения точки |
107 |
Относительное равновесие тел вблизи поверхности Земли |
110 |
Относительное движение тел вблизи поверхности Земли |
112 |
Лекция 14. . Введение в динамику механической системы
116 |
|
Свойства внутренних сил |
117 |
Центр масс механической системы |
118 |
Моменты инерции |
119 |
Лекция 15. Общие теоремы динамики |
124 |
Дифференциальные уравнения движения механической системы |
124 |
Теорема о движении центра масс |
125 |
Количество движения материальной точки. Теорема об |
|
изменении количества движения материальной точки |
127 |
Количество движения механической системы. Теорема об |
|
изменении количества движения механической системы |
129 |
Лекция 16. Момент количества движения материальной точки и |
|
механической системы |
133 |
Теорема об изменении кинетического момента |
|
механической системы |
136 |
Лекция 17. Теоремы об изменении кинетической энергии |
139 |
Работа силы. Мощность |
139 |
Лекция 18. Кинетическая энергия материальной точки |
|
и механической системы |
147 |
Теоремы об изменении кинетической энергии |
149 |
Лекция 19. Динамика твердого тела |
152 |
Дифференциальные уравнения движения твердого тела |
152 |
Физический маятник |
155 |
Лекция 20. Принцип Даламбера |
157 |
Принцип Даламбера для материальной точки |
157 |
Принцип Даламбера для механической системы |
158 |
Приведение сил инерции твердого тела |
161 |
Динамические реакции подшипников |
163 |
Лекция 21. Принципы аналитической механики |
167 |
Классификация связей |
167 |
Возможные перемещения. Возможная работа |
168 |
Принцип возможных перемещений |
172 |
Общее уравнение динамики |
174 |
Лекция 22 . Обобщенные координаты и обобщенные силы |
176 |
Принцип возможных перемещений в обобщенных |
|
координатах |
179 |
Лекция 23. Уравнения Лагранжа второго рода |
181 |
Принцип Гамильтона-Остроградского |
186 |
Лекция 24. Малые свободные колебания системы около |
|
положения устойчивого равновесия |
192 |
Свободные колебания механической системы |
|
с одной степенью свободы |
199 |
Лекция 25. Свободные колебания механической системы |
|
с двумя степенями свободы |
202 |
Лекция 26. Элементарная теория удара |
207 |
Основное уравнение удара |
207 |
Общие теоремы теории удара |
208 |
Коэффициент восстановления при ударе |
210 |
Удар тела о неподвижную преграду |
|
211 |
|
Прямой центральный удар двух тел (удар шаров) |
213 |
Потеря кинетической энергии при неупругом ударе |
|
двух тел. Теорема Карно |
215 |
Библиографический список |
217 |
МОДУЛЬ 1. КИНЕМАТИКА
ЛЕКЦИЯ 1
Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием механического движения и механического взаимодействия материальных тел. Механическим движением называется происходящее с течением времени изменение взаимного положения материальных тел в пространстве. Механическим взаимодействием называются действия материальных тел друг на друга, в результате которых происходит изменение движения этих тел или изменение их формы. Примерами механического движения в природе служат движения небесных тел, колебания земной коры, воздушные и морские течения, а в
технике движение всех видов транспорта, частей механизмов и машин, течение жидкостей и газов и т. д.
Наука о механическом движении и взаимодействии материальных тел называется механикой. Круг проблем, рассматриваемых в механике, велик. Поэтому существует целый ряд самостоятельных наук, изучающих те или иные формы механического движения: теории упругости и пластичности, гидромеханика, аэродинамика, сопротивление материалов, теория механизмов и машин и другие. Однако все они, не смотря на специфику, опираются на ряд законов и принципов, используют многие понятия и методы, общие для всех областей механики. Рассмотрение этих общих понятий, законов и методов составляет предмет теоретической механики.
В основе механики лежат законы (аксиомы), которые установлены путем обобщения результатов многочисленных опытов и наблюдений и нашли подтверждение в процессе общественно-производственной практики человечества. Это позволяет рассматривать знания, основанные на законах механики, как объективные и достоверные, которые инженер может смело использовать в своей практической деятельности.
Теоретическая механика имеет дедуктивный характер. Опираясь на аксиомы, как на проверенный практикой и экспериментом фундамент, она возводит свое здание науки с помощью строгих математических выводов.
Теоретическая механика как часть естествознания, использующая математические методы, имеет дело не с реальными материальными объектами, а с их моделями. Такими моделями являются:
1)материальная точка частица материи, размером которой можно пренебречь при изучении ее движения;
2)система материальных точек выделенная каким-либо образом совокупность материальных точек, движение которых изучается;
3)абсолютно твердое тело тело, расстояние между любыми точками которого не изменяется.
Кинематикой называется раздел теоретической механики, в котором изучают геометрические свойства движения тел без учета действующих на них сил.
Механическое движение происходит в пространстве и во времени. В теоретической механике в качестве моделей реальных пространства
ивремени выбраны абсолютное пространство и абсолютное время,
существование которых постулируется.
Абсолютное пространство представляет собой трехмерное, однородное и изотропное неподвижное евклидово пространство.
Абсолютное время считается непрерывно изменяющейся величиной, оно течет из прошлого к будущему. Время однородно, одинаково во всех точках пространства и не зависит от движения материальных тел. Абсолютное пространство и абсолютное время считаются независимыми одно от другого. Движение имеет относительный характер, изучается движение одного тела относительно другого неподвижного тела, с которым связывают неподвижную ортогональную систему координат. Такая система отсчета называется абсолютной, а движение тела относительно ее абсолютным движением.
Задачи кинематики состоят в разработке способов задания движения
иметодов определения скорости, ускорения и других кинематических величин как тела в целом, так и каждой его точки в отдельности.
КИНЕМАТИКА ТОЧКИ
Для задания движения точки применяется один из следующих способов: векторный, координатный или естественный.
Векторный способ
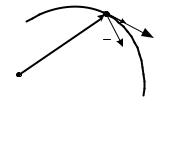
Рассмотрим движение точки М относительно заданного неподвижного центра О. Положение точки М в произвольный момент времени t можно определить, задав ее радиус-вектор r , проведенный из центра О в точку М, как вектор-функцию времени:
|
r r t . |
(1.1) |
|
M |
|
|
|
|
|
|
|
r |
dr |
|
|
|
|||||
Уравнение (1.1) называется уравнением движения |
a |
|
|
V |
|
|||||
O |
|
|
|
|
|
|
||||
точки в векторной форме. При движении точки М |
|
|
|
|
|
|
|
|||
конец радиус-вектора |
r описывает |
кривую, |
|
|
|
|
|
|
|
|
называемую траекторией точки. |
|
Рис. 1.1 |
|
|
|
|||||
Скоростью точки М в момент времени t |
|
|
|
|||||||
называется вектор V |
равный производной от |
|
|
|
|
|
|
|
|
|
радиус-вектора r по времени: |
|
|
|
|
|
|
|
dr |
|
|
|
V |
|
|
. |
(1.2) |
|
dt |
|||||
|
|
|
|

Вектор скорости характеризует изменение радиус-вектора точки в единицу времени по модулю и направлению. Вектор скорости V направлен
так же, как вектор |
элементарного перемещения dr по касательной к |
|
траектории |
|
в данной точке М (рис. 1.1). Размерность скорости |
V L / T , |
где L длина, Т время. Единицами измерения скорости могут |
|
быть м/c, cм/c, км/ч.
Ускорением точки М в момент времени t называется вектор а, равный производной от вектора скорости V точки, по времени:
|
|
dV |
|
|
а |
|
|
. |
(1.3) |
dt |
||||
Вектор ускорения характеризует изменение вектора скорости точки в единицу времени по модулю и направлению. Вектор ускорения а направлен в точке М в сторону вогнутости траектории (рис. 1.1). Размерность
ускорения а L / T 2 , поэтому оно измеряется в м/с2 или см/с2. Если угол между векторами V и а острый, то движение точки ускоренное, а если угол
тупой, то замедленное. Если угол между векторами V и а равен 90°, то точка равномерно движется по траектории.
Координатный способ
Z z
z 

|
|
M(x,y,z) |
|
r |
V |
|
|
a |
k |
j |
y Y |
O |
x |
i |
|
X
Рис. 1.2
уравнений (1.4). Учитывая связь
С точкой О свяжем неподвижную ортогональную декартовую систему координат ОXYZ и зададим координаты точки М(x, y, z) как функции времени:
x x(t), |
y y(t), |
z z(t) . (1.4) |
Уравнения (1.4) называются
уравнениями движения точки в декартовых координатах. Уравнение траектории точки можно определить исключением времени t как параметра из
r xi yj zk ,
(i , j, k единичные орты декартовых осей OX, OY, OZ на рис. 1.2),
определения (1.2) и (1.3), найдем скорость и ускорение точки в декартовых координатах:
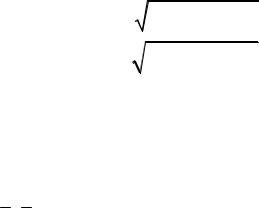
r |
|
dx r |
|
dy |
r |
dz r |
|
r |
r |
r |
(1.5) |
||||||
V |
dt |
i |
dt |
|
j |
dt |
k |
Vxi |
Vy j Vzk , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r |
|
d 2 x r |
|
d 2 y r |
|
d 2 z r |
|
r |
r |
r |
(1.6) |
||||||
a |
dt |
2 |
i |
dt |
2 |
j |
dt |
2 k |
axi |
ay j |
azk . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из (1.5) и (1.6) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Vx x,& Vy y,& |
Vz |
z;& |
|
(1.7) |
||||||||
|
|
|
|
|
ax &x, |
|
ay &y, |
az &z . |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
Проекции вектора скорости точки на декартовые оси равны первым производным, а проекции вектора ускорения вторым производным соответствующих координат по времени. В (1.7) и далее производная по
|
|
dA |
времени обозначается точкой, стоящей над величиной |
А |
. |
|
|
dt |
Скорость и ускорение точки по величине определяется по формулам:
V Vx 2 Vу2 Vz 2
a |
ax 2 |
aу2 |
az 2 |
(1.8) |
|
Направление векторов V и а найдем с помощью косинусов направляющих углов с осями OX, OY, OZ:
cos V i Vx ,V
r |
|
|
|
a |
|
|
|||
cos a |
i |
|
ax , |
|
|
|
|
|
|
r r |
|
V |
y |
|
|||
cos V |
j |
|
|
, |
|||
V |
|||||||
|
|
|
|
||||
r |
r |
|
ay |
|
|||
cos a |
j |
|
|
|
, |
||
a |
|||||||
|
|
|
|
|
|
|
|
r r |
Vz ; |
||||
cos V |
k |
||||
|
|
|
|
V |
|
r |
r |
|
(1.9) |
||
|
a |
||||
cos a |
|
k |
z |
. |
|
|
a |
||||
|
|
|
|
|
|
Естественный способ
Для задания движения точки естественным способом необходимо:
1)знать траекторию движения точки;
2)выбрать на траектории начало отсчета «О»;
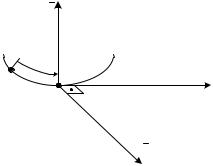
3)установить положительное и отрицательное направление отсчета криволинейной координаты s ОМ;
4)задать закон изменения криволинейной координаты s как функции времени:
s s(t) .
|
n |
Главная |
(_) |
|
нормаль |
s |
(+) |
|
О |
Касательная |
|
|
М |
Бинор |
|
|
|
|
|
м |
|
|
аль |
|
|
b |
Свяжем с точкой М естественный трехгранник,r r образованный единичными
векторами τ, n, b , составляющими правую
тройку ( |
|
r |
|
|
|
r |
|
|
|
b |
|
1) (рис. |
1.3); вектор |
τ |
|
|
|
|
|
|
|||||||||
|
|
|
|
n |
|
|
|
|||||||
направим |
|
в |
|
точке М по |
касательной |
к |
||||||||
траектории в сторону положительного отсчета s ОМ; вектор n по главной нормали к
|
центру кривизны траектории; вектор b по |
Рис. 1.3 |
бинормали к траектории. |
|
Радиус вектор r точки М относительно |
начала декартовой системы координат будет сложной функцией времени: |
|||||||
r r s t . Поскольку |
|
dr |
|
ds , то |
из |
дифференциальной |
геометрии |
|
|
||||||
известно, что ] |
|
|
|
|
|
||
|
|
dr |
|
r |
dτ |
1 r |
|
|
|
ds |
|
τ, |
ds |
ρ n , |
(1.10) |
где ρ радиус кривизны траектории в точке М. Используя (1.2), (1.10) и правило вычисления производной от сложной функции, получаем
r |
|
dr(s(t)) |
dr |
ds |
ds |
r |
V |
|
dt |
ds |
dt |
dt |
τ |
или |
|
|
|
|
|
|
V |
|
r |
&r |
(1.11) |
|
V τ |
s τ, |
||
где числовое значение скорости |
|
|
|
|
|
|
V |
& |
(1.12) |
|
|
s . |
Числовое значение скорости точки равно первой производной от криволинейной координаты s по времени.
Из (1.11) следует, что вектор скорости точки V направлен по касательной к траектории вдоль орта τ (в сторону положительного отсчета s), если s 0 (рис. 1.4), и против орта τ, если s 0 .
Дифференцируя (1.11) по времени, найдем ускорение точки при естественном способе задания движения:
