
Кинематика
.pdf
аналитическими условиями равновесия для произвольной пространственной системы сил.
Для равновесия твердого тела под действием произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.
2. Пространственная система
|
|
|
|
z |
|
|
|
|
|
параллельных сил. Для определенности |
|
||||||||||
|
|
|
|
|
|||||||||||||||||
Fn |
|
|
|
|
|
|
|
|
|
|
|
|
|
выберем систему координат так, чтобы ось |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оz была направлена |
параллельно |
силам |
|
||
|
|
|
|
|
|
|
|
|
F1 |
|
(рис. 8.8). В этом случае уравнения 1, 2 и 6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
O |
|
|
|
|
y в (8.18) отсутствуют, так как обращаются в |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тождества, |
и аналитические условия |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равновесия принимают вид |
|
|
|
||
x |
|
F3 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
r |
|
r |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Рис. 8.8 |
|
n |
n |
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fкz 0; |
mx (Fк ) 0; |
m y (Fк ) |
0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к 1 |
к 1 |
|
к 1 |
(8.19) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для равновесия твердого тела под действием пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю.
3. Пространственная система сходящихся сил (рис. 8.9). В этом случае за центр приведения выберем точку О, в которой пересекаются линий действия сил. Тогда уравнения 4, 5 и 6 системы (8.18) отсутствуют, и аналитические условия равновесия для пространственной системы сходящихся сил имеют вид
|
|
|
n |
|
|
z |
|
|
Fкx |
0; |
|
|
|
|
к 1 |
|
|
|
|
|
n |
|
|
Fn |
F |
|
Fкy |
0; |
(8.20) |
|
к 1 |
|
|||
|
1 |
y |
|
|
|
|
|
n |
|
|
|
O |
|
|
Fкz |
0. |
|
|
|
F2 |
к 1 |
|
|
F3 |
|
|
|
|
|
|
Для |
равновесия твердого |
тела под |
||
x |
|
||||
|
|
действием |
пространственной |
системы |
|
Рис. 8.9 |
сходящихся сил необходимо и достаточно, |
|
чтобы суммы проекций сил на каждую из |
||
|
||
|
трех координатных осей были равны нулю. |

ЛЕКЦИЯ 9
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
Пусть на |
абсолютное |
|
твердое |
тело |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Fn |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
действует |
пространственная |
система |
|
|
|
|
|
|
A n |
|
A2 |
|
F2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
параллельных |
|
сил |
|
|
F1 |
, F2 , F3 |
, ..., Fn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Fк |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
направленных в одну сторону (рис. 9.1). |
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
Aк |
|
|
|
rn |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Упростим эту систему сил, приведя ее |
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
rк |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|||||||||||||||||||||||
к произвольному центру |
О, |
причем |
точка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
приложения к-й силы Fк определяется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
относительно |
|
неподвижного |
|
центра |
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
радиус-вектором rк (к = 1, 2, …, n). |
данная |
|
|
|
|
|
|
|
|
|
Рис. 9.1 |
|
|
|
|
|
|
||||||||||||||||||||||
Согласно |
теореме |
Пуансо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
система сил |
F1 |
, F2 , F3, ..., Fn |
|
эквивалентна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одной силе R |
|
Fк , приложенной в центре О, |
и паре сил с моментом (рис. |
||||||||||||||||||||||||||||||||||||
9.2) |
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
n r |
|
|
r |
|
n |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
О |
|
m |
О |
(F ) |
|
r |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.1) |
|||||||||
|
|
|
|
|
|
|
|
к |
|
к |
к . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
к 1 |
|
|
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так |
как |
все |
|
|
силы |
|
|
F1 |
, F2 , F3, ..., Fn |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
параллельны друг |
другу |
и направлены |
в |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
одну |
сторону, |
|
то |
|
|
главный |
|
|
вектор |
R |
|||||||||||||||||
MO |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
R |
|
|
|
|
|
параллелен |
любой |
силе Fк , |
а его модуль |
|||||||||||||||||||||||||
|
|
О |
|
|
|
|
|
|
|
|
|
равен сумме модулей действующих сил |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R Fк , |
|
|
|
(9.2) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 9.2 |
|
|
|
|
|
|
|
где Fк |
модуль к-й силы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Главный |
момент |
МО |
|
системы |
сил |
относительно |
центра |
О будет |
|||||||||||||||||||||||||||||||
перпендикулярен главному вектору R , поскольку он равен геометрической |
|||||||||||||||||||||||||||||||||||||||
сумме коллинеарных |
|
векторов |
|
mО (Fк) , каждый |
|
|
|
|
|
из |
|
которых |
|||||||||||||||||||||||||||
перпендикулярен вектору соответствующей силы Fк , т. е. |
перпендикулярен |
||||||||||||||||||||||||||||||||||||||
вектору R (рис. 9.2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

Заменим главный момент МО парой сил R , R , лежащих в
перпендикулярной ему плоскости, такой, что R R , а R R (рис. 9.3). При этом
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
МО ОС R , |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
O |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rк Fк rC R , |
|
|
(9.3) |
|||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к 1 |
|
|
|
|
|
|
|
|
|
|
|
О 90О |
|
|
|
R = R |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
rC |
радиус-вектор |
точки |
С. |
||||
|
|
|
|
|
|
r |
|
C |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
Фактически |
формула |
(9.3) |
|
выражает |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теорему |
Вариньона |
для системы |
сил |
|||||
|
|
|
|
|
Рис. 9.3 |
|
|
|
|
|
|
F1, F2 |
, F3 |
, ..., Fn . Но силы |
R |
и |
R |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
образуют уравновешенную систему сил, |
||||||||
которая согласно аксиоме 2 статики может быть отброшена. |
F1, |
F2 |
, F3, |
..., Fn |
|||||||||||||||||||
|
|
Следовательно, |
|
любая система |
параллельных |
сил |
|||||||||||||||||
эквивалентна одной силе ( R R ) их равнодействующей, приложенной в точке С. Очевидно, что если повернуть параллельные силы F1, F2 , F3, ..., Fn около точек их приложения А1 , А2 , ..., Аn в одну и ту же сторону на один и
тот же угол, то их равнодействующая R повернется в точке С в ту же сторону на тот же угол.
Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол, называется центром параллельных сил.
Для определения положения точки С введем единичный вектор е ( е 1) по направлению к-й силы Fк Fке .
Тогда
|
|
|
|
r |
|
r |
|
n |
|
r |
|
|
|
|
|
|
R |
R Fкe ; |
|
||||||
|
|
|
|
|
|
|
|
к 1 |
|
|
|
|
r |
|
|
n |
r |
|
r |
|
n |
r |
|
r |
|
М |
О |
|
r |
F |
|
r |
F e. |
(9.4) |
||||
|
|
к |
|
к |
|
к |
|
к |
||||
|
|
|
к 1 |
|
|
|
|
к 1 |
|
|
|
|
С учетом (9.4) формула (9.3) принимает вид |
|
|
|
|||||||||
|
|
|
n |
r |
|
r |
|
r |
|
n |
r |
|
|
|
|
к |
|
к |
|
С |
|
|
к |
|
|
|
|
|
|
r |
F e r |
|
F e |
|
||||
|
|
|
к 1 |
|
|
|
|
|
|
к 1 |
|
|

или
n
Fк
к 1
Отсюда получаем
r |
|
r |
n |
F |
r |
r |
r |
e |
|
r |
e 0. |
||
к |
|
|
к |
С |
|
|
|
|
|
к 1 |
|
|
|
|
n |
r n |
|
Fк rк Fк |
|
|
к 1 |
к 1 |
r |
r |
(9.5) |
rС |
e 0. |
|
|
|
|
Поскольку векторное произведение в (9.5) равно нулю при произвольном направлении единичного вектора е , то формула (9.5) имеет место, если вектор
n |
r |
n |
r |
Fк rк Fк rС 0. |
|||
к 1 |
|
к 1 |
|
Отсюда определяем радиус-вектор rC центра С параллельных сил:
|
|
n |
r |
|
n |
r |
|
|
r |
|
Fк rк |
|
Fк rк |
|
|||
|
к 1 |
|
|
к 1 |
|
|
|
|
r |
|
|
|
|
. |
(9.6) |
||
|
|
R |
|
|||||
С |
|
n |
|
|
|
|
||
|
|
Fк |
|
|
|
|
|
|
к 1
Отметим, что все полученные выше формулы будут справедливы для системы параллельных сил, направленных в противоположные стороны, если
Fк считать алгебраическими величинами ( Fк >0, если сила Fк параллельна
единичному вектору е , и Fк < 0, если вектор
n
е и R Fк 0 .
к 1
Центр тяжести твердого тела
Вблизи поверхности Земли на каждую материальную частицу тела действует сила тяжести (сила притяжения), направленная по вертикали вниз. Так как размеры тела малы по сравнению с радиусом Земли, то
силы тяжести частиц тела Р1, Р2 , Р3, ..., Рn можно считать параллельными друг другу и
Fк направлен противоположно
z 
Pn |
P2 |
|
C |
||
|
P
О
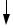 P1 y
P1 y
x
Рис. 9.4
постоянными по модулю для каждой частицы тела при любых его поворотах
(рис. 9.4).
Равнодействующая сил тяжести Р1, Р2 , Р3, ..., Рn частиц тела называется весом тела Р , модуль которой определяется согласно (9.2):
n |
|
P Pк . |
(9.7) |
к 1
Центром тяжести твердого тела называется геометрическая точка С, являющаяся центром параллельных сил тяжести Р1, Р2 , Р3, ..., Рn ,
действующих на частицы тела при любых поворотах тела в пространстве.
Согласно (9.6) положение центра тяжести С тела определяется радиусвектором
|
Pк rк |
|
|
|
|
n |
|
|
|
rС |
к 1 |
. |
(9.8) |
|
P |
||||
|
|
|
Тогда декартовые координаты точки С находится по формулам:
|
n |
|
|
n |
|
|
n |
|
|
|
xС |
Pк xк |
; |
yС |
Pк yк |
; |
zС |
Pк zк |
, |
|
|
к 1 |
к 1 |
к 1 |
(9.9) |
|||||||
P |
P |
P |
||||||||
|
|
|
|
|
|
|
где xк , yк , zк декартовые координаты точек приложения сил тяжести Pк , действующих на частицы тела. Для однородного тела объемом V вес Pк любой его части объема Vк составляет
Рк γ Vк , |
(9.10) |
|
где γ вес единицы объема, а вес всего тела |
|
|
n |
n |
|
P Pк γ Vк γ V . |
(9.11) |
|
к 1 |
к 1 |
|
Подставив (9.10) и (9.11) в (9.9), получим координаты центра тяжести однородного тела:
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
|
|
x |
|
γ Vк xк |
|
|
γ Vк xк |
|
|
Vк xк |
||||||
|
к 1 |
|
к 1 |
|
|
|
|
к 1 |
|
; |
||||
|
|
|
|
|
|
|
||||||||
С |
|
|
γ V |
|
|
γ V |
|
|
|
V |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
n |
|
|
|
|
|
|
n |
(9.12) |
||
|
y |
|
|
Vк yк |
; |
z |
|
|
Vк zк |
. |
|
|||
|
|
к 1 |
|
С |
к 1 |
|
||||||||
|
|
|
|
|
|
|||||||||
|
С |
|
V |
|
|
|
|
|
|
V |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку положение центра тяжести С однородного тела не зависит
от объемной плотности вещества , а определяется только геометрической формой тела, то точка С называется центром тяжести объема V.
Проводя аналогичные рассуждения для однородной плоской пластины
n
площади S Sк , получим ее координаты центра тяжести:
к 1 |
|
|
|
|
|
|
|
n |
|
|
n |
|
|
x |
Sк xк |
; |
y |
Sк yк |
|
|
к 1 |
к 1 |
, |
(9.13) |
|||
|
|
|||||
С |
S |
|
С |
S |
||
|
|
|
|
|
||
где xк , yк координаты к-й части пластины площади |
Sк . Формулы (9.13) |
|||||
определяют координаты центра тяжести площади S. Точно так же можно найти координаты центра тяжести линии длиной L:
|
|
n |
к |
|
к |
|
|
|
n |
к |
|
к |
|
|
n |
к |
|
к |
|
||
|
|
|
x |
|
|
|
|
y |
|
|
|
z |
|
||||||||
x |
|
l |
|
|
|
y |
|
l |
|
|
|
z |
|
l |
|
|
|
|
|||
|
к 1 |
|
|
|
; |
|
к 1 |
|
|
|
; |
|
к 1 |
|
|
|
. |
(9.14) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
С |
|
L |
|
|
|
С |
|
L |
|
|
|
С |
|
L |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рассмотрим некоторые способы определения координат центров тяжести однородных тел.
1.Способ симметрии. Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести С лежит соответственно в плоскости, на оси или центре симметрии тела.
2.Способ разбиения. Если однородное тело можно разбить на конечное число частей, положения центров тяжести которых известны, то координаты центра тяжести всего тела можно определить по формулам (9.12) – (9.14), где n соответствует числу частей, на которые разбивается тело.
3.Способ дополнения. Этот способ применяется к телам, имеющим вырезы, когда объем (площадь) данного тела можно представить как разность объемов (площадей) тел. Причем положения центра тяжести тела без выреза и вырезанной части известны. В этом случае объем (площадь) тела без выреза считается положительным, а объем (площадь) вырезанной части – отрицательным.

4. Способ интегрирования. Если тело нельзя разбить на конечное число частей, положения центров тяжести которых известны, то его разбивают на бесконечное число элементарных объемов (площадей, линий). Тогда координаты центров тяжести тел можно получить с помощью формул (9.12)
– (9.14), в которых суммы переходят в соответствующие интегралы. Приведем без доказательств координаты центров тяжести некоторых
однородных тел.
1. Центр тяжести С площади треугольника (рис. 9.5, а) лежит в точке пересечения его медиан, причем тока С делит каждую медиану в отношении
2 : 1, т. е.
CE |
1 BE. |
(9.15) |
|
3 |
|
2. Центр тяжести С дуги окружности радиусом R с центральным углом 2α (рис. 9.5, б) лежит на оси ее симметрии на расстоянии от центра О равном
|
|
xC OC |
R sin α . |
|
|
|
(9.16) |
|
|
|
|
α |
|
|
|
|
|
|
3. Центр тяжести С площади кругового сектора радиусом R с |
|||||||
центральным углом 2α (рис. 9.5, в) лежит на |
оси его |
симметрии на |
||||||
расстоянии от центра О равном |
|
|
|
|
|
|
||
|
|
xC OC |
2R sin α . |
|
|
(9.17) |
||
|
|
|
|
3α |
|
|
|
|
|
|
B |
B |
|
|
|
|
B |
|
|
R |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
C |
O α |
C |
x |
O |
α |
C |
x |
|
α |
|
|
|||||
A |
|
α |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
A |
|
|
|
|
|
|
|
|
||
|
|
а |
б |
|
|
в |
|
|
|
|
Рис. 9.5 |
|
|
|
|
|
|

4. Центр тяжести С объема конуса (рис. 9.6, а) или призмы лежит на отрезке прямой ЕС1, соединяющей вершину Е конуса с центром тяжести С1 его основания, причем
E |
z |
|
|
|
|
R |
C |
|
|
|
C |
C1 |
|
|
|
O |
a |
|
|
|
б |
|
Рис. 9.6 |
|
||
CС1 |
|
1 |
EС1. |
(9.18) |
|
|
4 |
|
|
5. Центр тяжести С объема полусферы радиусом R (рис. 9.6, б) лежит на оси симметрии Оz с координатой
zC = OC = 3R/8.

МОДУЛЬ 3. ДИНАМИКА
ЛЕКЦИЯ 10
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Законы классической механики
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.
Первоначально при изучении динамики, для того чтобы отвлечься от учета влияния формы тела на его движение, рассмотрим динамику материальной точки. В ее основе лежат законы (аксиомы динамики), впервые наиболее полно сформулированные Исааком Ньютоном в его сочинении «Математические начала натуральной философии» в 1687 году.
I закон (принцип инерции): изолированная от внешнего воздействия материальная точка находится в состоянии покоя или равномерного и прямолинейного движения. При изучении движения материальных тел важным обстоятельством является выбор системы отсчета. Согласно принципу инерции существует система отсчета, в которой материальная точка находится в состоянии покоя или движется равномерно и прямолинейно, если на нее не действуют силы. Система отсчета, в которой выполняется принцип инерции, называется инерциальной (иногда ее условно называют неподвижной).
II закон (основной закон динамики): сила, действующая на свобод-
ную материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине силы и имеет направление силы
(рис. 10.1): |
r |
F , |
|
|
|
|
|
|
|
|
|
||
|
|
(10.1) |
|
|
|
|
|
|
|
|
|||
|
|
m a |
|
|
|
M |
|||||||
где F |
вектор силы, |
действующей на точку; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||
m ее масса; |
a ускорение точки. |
|
|
|
|
|
|
|
|
|
|||
основным |
O |
|
|
V |
|
||||||||
|
|
||||||||||||
Уравнение (10.1) |
|
называется |
|
|
|||||||||
урав-нением динамики точки. Масса m является, |
|
|
F |
||||||||||
ме-рой ее инертности, т. е. способности точки |
Рис. 10.1 |
||||||||||||
«сопро-тивляться» изменению ее скорости. |
|
|
|
|
|
|
|
|
|||||
Масса |
пред-ставляет |
собой |
основную |
|
|
|
|
|
|
|
|
||
динамическую характеристику материальной точки. |
|
|
|
|
|
|
|
|
|||||
Согласно закону (10.1) устанавливается соотношение между массой |
|||||||||||||
тела m и его весом P: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
mg P , |
(10.2) |
|||||||
где g ускорение свободного падения.

III закон (закон равенства действия и противодействия): две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
IV закон (закон независимости действия сил): если на материальную точку действует несколько сил, то ускорение точки складывается из тех ускорений, которые имела бы точка под действием каждой из этих сил в отдельности:
|
|
|
|
|
|
a a1 a2 ... an , |
|
|
(10.3) |
||||||||
где a полное ускорение точки; |
a1, |
a2 ,..., an ускорения, сообщаемые |
|||||||||||||||
точке соответственно силами F1, |
F2 , |
... , Fn . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании II и IV законов |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно сделать вывод о том, что если |
|||
|
|
|
F1 |
|
|
|
|
|
на материальную точку действует n |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сил, то точка получает ускорение, |
|||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
пропорциональное |
геометрической |
||
1 |
|
|
|
|
|
|
F2 |
|
сумме этих сил и направленное так |
||||||||
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
же, как и их |
равнодействующая R |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
m |
|
|
|
|
|
(рис. 10.2): |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
a |
3 |
|
|
|
|
|
|
|
|
n |
|
|
||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
ma Fк |
R . |
(10.4) |
|
|
|
|
|
|
|
|
|
|
F3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
к 1 |
|
|
||||
|
|
|
|
|
|
R |
|
|
|
|
|
|
Движение материальной точки под |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действием сил F1, |
F2 , ... , Fn |
будет |
|
|
Рис. 10.2 |
|
|
|
|
|
таким же, как и при действии на нее |
||||||||||
их равнодействующей R .
Если рассматривается движение несвободной материальной точки, то, применяя принцип освобождаемости от связей, ее можно рассматривать как свободную, включив в состав действующих на нее активных (заданных) сил и силы реакций связей.
В этом случае для точки справедливы указанные выше законы
|
F N , где |
F, N соо- |
динамики. В частности (10.4) принимает вид m a |
тветственно равнодействующие активных сил и реакций связей, действующих на точку.
Дифференциальные уравнения движения материальной точки
