
Термодинамика и теплопередача в технологических процессах нефтяной и газовой промылшенности
.pdfТермодинамика в технологических процессах… |
31 |
Это выражение (1.84) впервые было получено Р. Майером (1842 г.) и назы-
вается законом Майера.
Уравнение (1.84) может быть записано и для одного кмоля газа
|
|
p − |
|
|
= µ (cp − cv ) = µ R = |
R |
. |
(1.85) |
|||||||
|
c |
cv |
|||||||||||||
Разделив уравнение (1.81) на абсолютную температуру T, получим |
|
||||||||||||||
δq = cv |
dT |
+ |
p |
dv = cp |
dT |
− |
v |
dp . |
(1.86) |
||||||
|
|
|
|
||||||||||||
T |
T T |
T T |
|
||||||||||||
С учетом того, что для идеального газа, исходя из уравнения Клапейрона,
справедливы равенства: |
p |
= |
R |
; |
|
v |
= |
R |
получим |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
T v |
T |
p |
|
|
|
|
|
|
|
|
|
||||||
δq = cv (T) |
dT |
+ R |
dv |
= cp |
(T) |
dT |
− R |
dp |
. |
(1.87) |
||||||||
|
|
T |
|
|||||||||||||||
T |
|
T |
|
|
v |
|
|
p |
|
|||||||||
Правая часть уравнения (1.87) представляет собой сумму полных дифференциалов. Это значит, что и соотношение δq /T есть полный дифференциал некоторой
функции состояния идеального газа (s), называемой удельной энтропией. Изменение удельной энтропии в элементарном процессе представляет собой
полный дифференциал и определяется соотношением
ds = δq = cv |
(T) |
dT |
+ R |
dv |
= cp |
(T) |
dT |
− R |
dp |
. |
(1.88) |
T |
|
T |
|
||||||||
T |
|
|
v |
|
|
p |
|
||||
Из уравнения (1.88) после интегрирования получим, что изменение удельной энтропии идеального газа в процессе 1–2 может быть найдено из соотношения
s |
2 |
− s = c ln |
T2 |
+ R ln |
v2 |
= c ln |
T2 |
+ R ln |
p1 |
. |
(1.89) |
|
|
|
|
|
|||||||||
|
1 |
mv |
T1 |
|
v1 |
mp |
T1 |
|
p2 |
|
||
|
|
|
|
|
|
|
|
|||||
Теплоемкости cmp и cmv называются вторыми средними теплоемкостями и находятся путем осреднения по логарифму абсолютных температур
|
|
1 |
2 |
|
cmz = |
|
∫cz d lnT . |
(1.90) |
|
ln |
− ln |
|||
|
T2 |
T1 |
1 |
|
Если принять, что истинная теплоемкость является линейной функцией температуры cz = az + bzT , то
|
∫2 (az |
+ bzT ) |
dT |
|
|
|
|
|
|
|
|
|||
cmz = |
T |
= az |
+ bz |
|
T2 − T1 |
= az + bz Tmz . |
(1.91) |
|||||||
1 |
|
|
|
|||||||||||
|
|
T |
|
|||||||||||
|
|
|
|
|
|
|
T |
|
|
|||||
|
|
ln |
2 |
|
|
|
|
ln |
2 |
|
|
|
||
|
|
T1 |
|
|
|
T1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||

32 |
Часть 1 |
Таким образом, первая средняя теплоемкость равна истинной теплоемкости при средней арифметической температуре процесса (Tma ), а вторая – при средней логарифмической температуре процесса (Tmz). В случае, если bz > 0 , то первая средняя теплоемкость численно несколько больше второй.
1.5. Процессы изменения состояния термодинамических систем
Классификация термодинамических процессов
Термодинамический процесс может быть задан либо графическим способом в виде изображения процесса в координатах p-v, p-T, Т-s, либо в аналитической форме в виде зависимости ϕ( p,v) = 0 .
Уравнение процесса может быть также задано исходным условием о неизменном значении в этом процессе какой – либо функции состояния или их комплекса ( z = idem; z = p,v, t, u, h, s ) или условием о равенстве нулю какого-либо
эффекта термодинамического процесса (δq = 0) .
Однако и в этом случае исходное условие приводится к основной форме уравнения процесса.
При изучении термодинамических процессов определяются:
1)закономерность изменения параметров состояния рабочего тела, то есть выводится уравнение процесса или дается его графическое изображение в координатах p-v, p-T, Т-s и т.д.;
2)параметры состояния системы в начальной и конечной точках процесса;
3)численные значения работы и теплообмена в процессе;
4)изменение значений внутренней энергии, энтальпии и энтропии рабочего
тела.
Простейшие термодинамические процессы
Простейшими термодинамическими процессами обычно считают изобарный, изохорный и изопотенциальные процессы.
Изобарный процесс – процесс, в котором давление в системе остается постоянным ( p = idem; dp = 0 ).
Изобарный процесс графически представлен на рисунке 1.7.
В изобарных процессах происходит увеличение (1–2) или уменьшение (1–3) удельного объема, что связано изменением температуры, обусловленным подводом или отводом теплоты.
Изобарные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых, холодильных установках и др.
Для идеального газа в изобарном процессе 1–2 значение удельного объема
прямо пропорционально температуре рабочего тела T2 = v2 .
T1 v1

Термодинамика в технологических процессах… |
33 |
Рис. 1.7. Простейшие термодинамические процессы:
1–2, 1–3 – изобары; 1–4, 1–5 – изохоры; 1–6, 1–7 – изопотенциальные процессы
Удельная термодинамическая и потенциальная работы в изобарном процессе определяются из соотношений
2 |
2 |
|
l1,2 = ∫ p dv = p (v2 |
− v1 ) , w1,2 = −∫ v dp = 0 . |
(1.92) |
1 |
1 |
|
В случае идеального газа в силу |
pv = RT имеем |
|
2 |
|
|
l1,2 = ∫ p dv = p (v2 − v1) = R(T2 − T1) . |
(1.93) |
|
1 |
|
|
Количество теплоты, подведенной к рабочему телу или отведенной от него в изобарном процессе, определяется из выражения первого начала термодинамики
q1,2 = u1,2 + l1,2 = h1,2 . |
(1.94) |
Изохорный процесс – процесс, при котором объем системы или удельный объем рабочего тела остается постоянным (v = idem; dv = 0 ) графически изобра-
жен на рисунке 1.7.
В изохорных процессах происходит уменьшение (1–5) или увеличение давления (1–4), что связано с соответственным изменением температуры – подводом или отводом теплоты.
Изохорные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых установках и др.
Для идеального газа в изохорном процессе 1–4 давление прямо пропорцио-
нально температуре рабочего тела T4 = p4 .
T1 p1

34 |
Часть 1 |
Удельная термодинамическая и потенциальная работы в изохорном процессе определяются из соотношений
4 |
4 |
|
l1,4 = ∫ p dv = 0; w1,4 = −∫vdp = v ( p1 − p4 ) . |
(1.95) |
|
1 |
1 |
|
В случае идеального газа в силу pv = RT |
имеем |
|
4 |
|
|
w1,4 = −∫∫12 vdp = v (p1 − p4 ) = R(T1 −T4 ) . |
(1.96) |
|
1 |
|
|
Количество теплоты, подведенной к рабочему телу или отведенной от него в изохорном процессе, определяется из выражения первого начала термодинамики
q1,4 = h1,4 + w1,4 = u1,4 . |
(1.97) |
Изопотенциальный процесс – термодинамический процесс изменения состояния системы (рисунок 1.7), при котором значение потенциальной функции сохраняет неизменное значение ( П = pv = idem; d( pv) = 0 ). Для идеального газа,
согласно уравнению Клапейрона ( pv = RT ), изопотенциальный процесс являет-
ся и изотермическим (T = idem ).
Удельная термодинамическая и потенциальная работы в изопотенциальном процессе 1–6 определяются из следующих соотношений:
6 |
6 |
|
dv |
|
|
|
v6 |
|
|
|
|
|
l1,6 = ∫ p dv = ∫ p v |
= pv ln |
; |
|
|
(1.98) |
|||||||
v |
v1 |
|
|
|||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|||
6 |
6 |
dp |
|
|
1 |
dp |
|
|
|
p |
|
|
w1,6 = −∫ v dp = −∫ vp |
|
= pv ∫ |
|
= pv ln |
1 |
. |
(1.99) |
|||||
p |
p |
p |
||||||||||
1 |
1 |
|
|
|
6 |
|
|
|
|
6 |
|
|
Нетрудно заметить, что постоянство потенциальной функции pv = idem приводит к равенству логарифмов в выражениях (1.98) и (1.99) в силу того, что соблюда-
ется условие p1 = v6 . Поэтому, в изопотенциальном процессе численные значения p6 v1
термодинамической и потенциальной работ равны между собой.
Количество теплоты, подведенной к рабочему телу или отведенной от него в изопотенциальном процессе определяется из выражения первого начала термодинамики по балансу рабочего тела
q1,2 = u1,2 + l1,2 = h1,2 + w1,2 . |
(1.100) |
Термодинамика в технологических процессах… |
35 |
Уравнения перечисленных простейших и любых других термодинамических процессов могут быть представлены одним уравнением. Это уравнение называется уравнением политропы, а термодинамические процессы, описываемые этим уравнением, называются политропными.
Политропные процессы
Термин «политропа» представляет собой сочетание двух греческих слов poly – много и tropos – путь, направление. Поэтому в политропном процессе предполагается многообразие путей изменения параметров состояния системы.
Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела, подчиняющийся уравнению, которое может быть представлено в следующих формах:
pvn |
= idem = C ; |
|
(1.101) |
||
p1/ n v = idem = C |
; |
(1.102) |
|||
|
|
|
1 |
|
|
p vn = |
p vn . |
|
(1.103) |
||
1 |
1 |
2 |
2 |
|
|
где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения – положительные и отрицательные (-∞≤ n≤ +∞).
Физический смысл показателя политропы п определяется после дифференцирования выражения (1.101)
vn dp + n vn−1 pdv = 0 . |
(1.104) |
||||||
Из этого соотношения непосредственно следует |
|
||||||
|
vdp |
|
δw |
|
w |
|
|
n = − |
|
= |
|
= |
1,2 |
. |
(1.105) |
|
δl |
|
|||||
|
pdv |
|
|
l |
|
||
|
|
|
|
1,2 |
|
|
|
Это значит, что постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах. Значения этих работ могут быть определены графически
вкоординатах p − v (рисунок 1.8а).
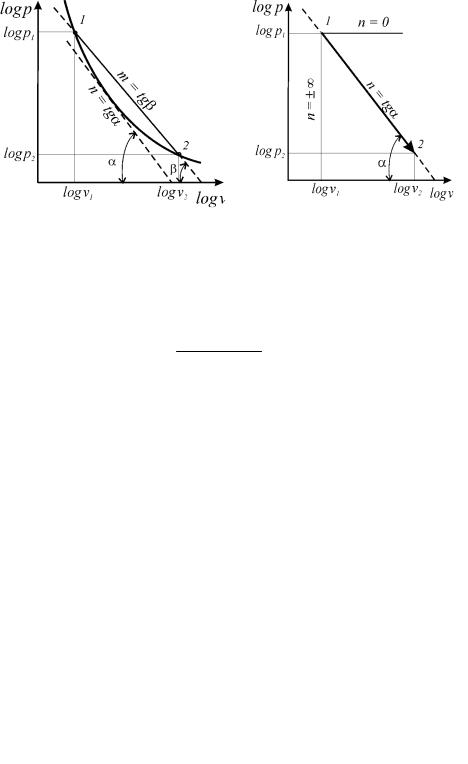
Влогарифмических координатах политропный процесс с постоянным показателем представляет собой прямую линию (рис. 1.8б)
log p + n logv = logC . |
(1.106) |
36 |
Часть 1 |
а |
б |
Рис. 1.8. Политропа с постоянным показателем
Постоянный показатель политропы определяется как тангенс угла α наклона линии процесса к оси абсцисс (рисунок 1.8б)
n = log p1 − log p2 = logv2 − logv1
log |
|
p1 |
|
|
|
|
|
p2 |
. |
(1.107) |
|||
|
|
|||||
|
|
|
||||
log |
v2 |
|
|
|
||
v1 |
|
|||||
|
|
|
||||
Из соотношения (1.104) следует, что для изобарного процесса n = 0, для изохорного процесса n = ± ∞, для изопотенциального процесса n = 1.
Следует отметить, что не все термодинамические процессы в координатах logv – logp описываются прямой линией, т.е. подчиняются уравнению политропы с постоянным показателем. Так процессы сжатия природного газа в центробежном нагнетателе трудно описать уравнением политропы с постоянным показателем [10, 21]. Любой термодинамический процесс можно описать уравнением
политропы с переменным показателем (рисунок 1.9).
Рис. 1.9. Политропа с переменным показателем

Термодинамика в технологических процессах… |
37 |
Расчет политропного процесса с переменным показателем вызывает необходимость ввести в рассмотрение три показателя процесса: истинный показатель
процесса n; первый средний показатель n и второй средний показатель m. Истинный показатель процесса n определяется как соотношение элементарной
потенциальной работы δw к элементарной термодинамической работе δl , что соответствует тангенсу угла наклона касательной, проведенной к кривой процесса в точке процесса, к оси абсцисс α в логарифмической сетке координат.
δw |
= − |
vdp |
= |
d log p |
|
|
n = δl |
|
|
= tgα. |
(1.108) |
||
pdv |
d logv |
|||||
Для конкретных процессов, характеризующихся неизменным значением какой-либо функции или параметра состояния (z = p, v, T, u, h, s), истинный показатель политропы определяется соотношением
|
|
v |
|
∂p |
|
nz |
= − |
|
|
. |
(1.109) |
|
|||||
|
|
p |
|
∂v z |
|
Первый средний показатель политропы определяется как отношение конечных (интегральных) значений потенциальной и термодинамической работ в процессе
|
|
= |
w1,2 |
. |
(1.110) |
|
n |
||||||
|
|
|||||
|
|
|
l1,2 |
|
||
Второй средний показатель политропы численно равен тангенсу угла наклона β секущей 1–2 к оси абсцисс в логарифмической сетке координат (рисунок 1.9)
m = |
log p1 − log p2 |
= |
log(p1 / p2 ) |
. |
(1.111) |
||
|
|
||||||
|
logv |
− logv |
|
log(v |
/ v ) |
|
|
|
2 |
1 |
|
2 |
1 |
|
|
Непосредственно из последнего выражения (1.111) следует уравнение политропы с переменным показателем
|
|
|
|
m |
|
|
|
1 |
|
|
|
|
|
p |
v |
|
p |
|
|
|
|
v |
|
|
|||
2 |
2 |
m |
|
|
|
||||||||
2 |
|
|
|
= |
|
|
|
2 |
= 1 . |
(1.112) |
|||
|
|
|
|
|
|
||||||||
p1 |
v1 |
p1 |
|
v1 |
|
|
|||||||
При проведении инженерных расчетов в ряде случаев политропные процессы с переменным показателем политропы приближенно описываются уравнением политропы с постоянным показателем (1.101), значение которого принимается равным первому среднему показателю политропы ( n = n ).
Работа в политропных процессах простых тел
Выражения конечных (интегральных) величин термодинамической и потенциальной работ в политропных процессах можно получить при сопоставлении их элементарных значений:
38 |
Часть 1 |
δl = pdv, δw = −vdp ; |
(1.113) |
δl − δw = pdv + vdp = d ( pv) . |
(1.114) |
После подстановки выражения для показателя политропы (1.105) в соотно-
шение (1.114) получаем |
|
|
|
|
|
δl − δw = (1− n) δl = d ( pv) , |
(1.115) |
||||
или |
|
|
|
|
|
δl = |
|
|
1 |
d ( pv) . |
(1.116) |
1 |
|
||||
|
− n |
|
|||
Интегрируя последнее выражение (1.116) с учетом того, что процесс подчиняется уравнению политропы с постоянным показателем n=idem, получаем следующее соотношение для определения удельной термодинамической работы в конечном процессе (1–2)
l = |
2 |
|
1 |
d( pv) = |
1 |
|
2 d(pv) = |
1 |
(p v |
− p v ) . |
(1.117) |
||
|
|
|
|
|
|||||||||
1,2 |
∫1 |
− n |
1− n |
|
∫ |
1− n |
2 |
2 |
1 |
1 |
|
||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
Введем понятие характеристики процесса расширения или сжатия, определяемой соотношением
τ = |
p2v2 |
. |
(1.118) |
|
|||
1,2 |
p1v1 |
|
|
|
|
||
С учетом соотношений (1.105), (1.118), зависимости для определения удельной термодинамической и потенциальной работы в конечном процессе принимают следующий вид:
|
|
|
l1,2 = |
p1v1 |
(1− τ1,2 ); |
|
|
|
(1.119) |
|||||||||||||
|
|
|
n −1 |
|
|
|
||||||||||||||||
w1,2 |
= n l1,2 |
= |
|
n |
|
|
p1v1 |
(1− τ1,2 ). |
(1.120) |
|||||||||||||
|
|
|
||||||||||||||||||||
n −1 |
||||||||||||||||||||||
Соотношение для определения |
|
характеристики |
расширения |
или сжатия |
||||||||||||||||||
в рассматриваемом процессе |
τ1,2 |
определяется с учетом зависимостей (1.101), |
||||||||||||||||||||
(1.102) и имеет следующий вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
v |
n−1 |
|
|
||
τ |
= |
|
p v |
|
|
|
p |
|
|
n |
|
|
|
|
||||||||
|
|
2 2 |
|
= |
|
|
|
|
2 |
|
|
= |
|
1 |
|
. |
(1.121) |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1,2 |
|
|
p1v1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
p1 |
|
|
v2 |
|
|
|
|||||||||||
Термодинамика в технологических процессах… |
39 |
Теплообмен в термодинамических процессах простых тел
Теплообмен в любом термодинамическом процессе изменения состояния простых тел может быть выражен в зависимости от величины термодинамической или потенциальной работы процесса. При этом термодинамический процесс в общем случае рассматривается как политропа с переменным показателем.
Расчетное выражение теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики
δq = du + δl. |
(1.122) |
Удельная внутренняя энергия для простых тел может быть представлена в виде функции любых двух независимых параметров состояния. Примем, что u =и(p, v). Тогда дифференциал внутренней энергии запишется в следующем виде:
|
∂u |
|
+ |
|
∂u |
dp . |
du = |
|
dv |
|
|
||
dv p |
|
dp v |
|
|||
Последнее выражение (1.123) можно представить в виде
|
1 |
|
∂u |
|
|
1 |
|
∂u |
|
du = |
|
|
|
pdv |
+ |
v |
|
|
vdp . |
|
|||||||||
|
p |
dv p |
|
|
dp v |
|
|||
Введем следующие обозначения:
(1.123)
(1.124)
|
1 |
∂u |
|
|
|
1 |
|
∂u |
|
av = |
|
|
|
; |
ap = |
|
|
. |
(1.125) |
|
|
||||||||
|
p |
dv |
p |
|
|
v |
dp v |
|
|
При этом выражение (1.124) примет вид: |
|
|
|
|
|||||
du = av δl − ap δw = av δl − ap n δl = (av − n ap ) δl . |
(1.126) |
||||||||
Сопоставляя соотношения (1.122) и (1.126), получим |
|
||||||||
|
|
δq = (av |
− n ap +1) δl. |
(1.127) |
|||||
Для определения величин av и ap рассмотрим два термодинамических про-
цесса:
1. Изоэнергетический процесс (u = idem, du = 0). Для этого процесса показатель политропы принимает значение n = nu.
Так как в изоэнергетическом процессе δl |
≠ 0 , из уравнения (1.126) следует |
||
av |
− nu ap = |
0 , |
(1.128) |
или |
av = nu ap . |
(1.128а) |
|
40 |
Часть 1 |
2. Адиабатный процесс (δ q = 0). В этом процессе показатель политропы принимает значение n = k и называется показателем адиабаты.
В адиабатном процессе элементарная термодинамическая работа также не равна нулю, поэтому из выражения (1.127) имеем
av − k ap +1= 0 . |
(1.129) |
Сопоставляя соотношения (1.128) и (1.129), получаем следующие выражения:
ap |
= |
1 |
, av |
= |
nu |
. |
(1.130) |
k − n |
|
||||||
|
|
|
|
k − n |
|
||
|
|
u |
|
|
u |
|
|
С учетом полученных соотношений для определения av и ap, находим выражения для расчета удельных значений изменения внутренней энергии и теплообмена в элементарном процессе:
du = |
nu − n |
δl |
, |
(1.131) |
||
k − n |
||||||
|
|
u |
|
|
|
|
δq = |
k − n |
δl . |
(1.132) |
|||
|
||||||
|
|
k − n |
|
|
|
|
|
|
u |
|
|
|
|
Соотношения для расчета удельных значений изменения внутренней энергии и теплообмена в конечном процессе имеют следующий вид:
u |
= |
|
nu − |
n |
|
l |
, |
(1.133) |
|||
k − n |
|
||||||||||
1,2 |
|
|
1,2 |
|
|
||||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
= |
k − |
|
|
l . |
|
|
||||
q |
n |
|
(1.134) |
||||||||
|
|
|
|
|
|||||||
1,2 |
|
k − n |
1,2 |
|
|
||||||
|
|
|
|
u |
|
|
|
|
|||
Полученные соотношения (1.133), (1.134) позволяют в координатах p-v построить области подвода и отвода теплоты, увеличения и уменьшения внутренней энергии (рисунок 1.10).
Некоторые характеристики важнейших термодинамических процессов приведены в таблице 1.2.
