Термодинамика и теплопередача в технологических процессах нефтяной и газовой промылшенности
.pdfТеплопередача в технологических процессах… |
151 |
|||
|
|
|
||
Подставляя решение (2.55) в уравнение (2.54) получим |
|
|||
U′(τ) P(x, y,z) = a U(τ) 2P(x, y,z). |
(2.56) |
|||
Уравнение (2.56) можно переписать так |
|
|||
U′(τ) |
= a |
2P(x, y, z) |
|
|
|
|
. |
(2.57) |
|
|
U(τ) |
|||
|
|
P(x, y, z) |
|
|
Левая часть уравнения (2.57) может зависеть только от τ или быть постоянным числом; она не зависит от координат. Правая часть может зависеть от координат или быть постоянным числом; она не зависит от времени. Поскольку уравнение (2.57) справедливо при любых значениях времени и координат, то правая и левая части его равны постоянной величине, которую обозначим через D.
Таким образом, мы получим два дифференциальных уравнения для опре-
деления вида функций U(τ) и P(x, y, z): |
|
|
||
|
U′(τ) |
= D ; |
a 2 P(x, y, z) = D . |
(2.58) |
|
||||
|
U(τ) |
P(x, y, z) |
|
|
Решением уравнения (2.58) является |
|
|||
|
|
U(τ) = C eDτ , |
(2.59) |
|
где С – постоянная интегрирования.
Постоянная величина D выбирается из физических соображений. В большинстве случаев при нагревании или охлаждении тел по истечении длительного времени температура распределяется в теле определенным образом. Для тепловых процессов, стремящихся к тепловому равновесию, величина D не может быть положительной, потому что можно задать такой промежуток времени, при котором температура в теле будет стремиться к бесконечности, что физически невозможно. Величина D не может равняться нулю, так как при D = 0 функция U(τ) в уравнении (2.59) имела бы постоянное значение, а температура тела не зависела бы от времени, как это следует из уравнения (2.55), что не реально.
Таким образом, из физических соображений следует, что величина D может быть отрицательной или мнимой величиной. Последний случай будет при условии, что температура тела есть периодическая функция времени, тогда экспонента (2.59) будет периодической функцией времени.
Рассматривая случай, когда D < 0, предположим, что
D = −а m2 , |
(2.60) |
где а – коэффициент температуропроводности (величина |
положительная); |
m – некоторая постоянная величина, определяемая из граничных условий.
152 |
Часть 2 |
|
|
С учетом (2.60) имеем выражение для функции U(τ) |
|
U (τ) = C e−a m2 τ . |
(2.61) |
Уравнение (2.58) для P(x, y,z) записывается следующим образом |
|
2P(x, y,z) + m2 P(x, y,z) = 0. |
(2.62) |
Методы решения уравнения (2.62) излагаются в курсах высшей математики. Исходя из того, что при заданных условиях однозначности решение уравнение (2.62) найдено и вид функции P(x, y, z) известен, частное решение урав-
нения (2.54) примет вид
t = C e− a m2 τ P(x, y, z). |
(2.63) |
Для общего решения уравнения (2.54) по принципу наложения берут сумму частных решений. Постоянная m определяется из граничных условий, а постоянная C – из начальных условий.
Метод источников. Метод источников заключается в замене процесса распространения теплоты в теле теплопроводностью совокупностью процессов выравнивания температуры от большого количества элементарных источников теплоты, распределенных в пространстве и времени.
Правильный выбор источников теплоты и их распределение во времени – необходимое условие получения надежного решения уравнения теплопроводности.
Сущность метода источников покажем на примере неограниченного тела при одномерном потоке теплоты. В этом случае действие элементарного источника характеризуется функцией источника на бесконечной прямой
G(x,τ,ζ) = |
|
|
b |
|
− |
(x − ζ)2 |
|
|
|
|
|
exp |
|
. |
(2.64) |
||
|
|
|
4 a τ |
|||||
4 |
a τ |
|
|
|
|
|||
Функция G представляет температуру в точке x, если в начальный момент времени в точке ζ выделяется теплота в количестве Q = b cр ρ. Количество теплоты на бесконечной прямой равно
|
|
b |
|
∞ |
|
|
(x − ζ)2 |
|
|
dx |
|
|
|
b c |
р |
ρ |
∞ |
2 |
|
||||||
Q = cр |
ρ |
|
|
|
∫ |
exp |
− |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
∫ |
e−u du = b cр |
ρ, (2.65) |
|
|
|
|
|
a τ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
||||||||||||||
|
|
|
π −∞ |
|
|
4 |
2 a |
τ |
|
|
|
−∞ |
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x−ζ |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
u = |
|
; |
|
e−u2 du = |
|
π . |
|
|
(2.65а) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 a τ |
|
−∞∫ |
|
|
|
|
|
|
|
|
|
|
|
|||
Теплопередача в технологических процессах… |
153 |
|
|
Функцию G называют фундаментальным решением уравнения теплопроводности, поскольку она удовлетворяет этому уравнению. В самом деле, для неограниченного тела при одномерном потоке теплоты уравнение (2.54) имеет вид
∂t |
= a |
∂2t |
. |
(2.66) |
|
|
|
||||
∂τ |
∂x2 |
||||
|
|
|
Если функция G является решением уравнения (2.66), его можно записать
так
∂G |
= a |
∂2G |
. |
|
|
|
(2.67) |
∂τ |
∂x2 |
|
|
|
|||
|
|
|
|
|
|
||
Пользуясь уравнением (2.64), найдем выражения для |
∂G |
и |
∂2G |
: |
|||
∂τ |
∂x2 |
||||||
∂∂τG = 
∂2G = ∂x2
b (x − ζ)2π τ 4 a τ 4 a
аb (x − ζ)2
π τ 4 a τ 4 a
|
1 |
|
|
|
(x − ζ)2 |
|
|
|||||
− |
|
|
|
exp − |
|
|
; |
(2.68) |
||||
|
|
|
|
|
||||||||
|
2 |
τ |
|
|
|
4 a τ |
|
|
||||
− |
|
|
1 |
|
|
|
− |
(x − ζ)2 |
|
|||
|
|
|
|
exp |
|
|
. |
(2.69) |
||||
|
|
|
|
|
|
|||||||
|
|
2 τ |
|
|
|
4 a τ |
|
|
|
|||
Сопоставление двух последних выражений показывает справедливость уравнения (2.67).
Преобразование Лапласа. Преобразование Лапласа приводит к операционному методу решения линейных и нелинейных дифференциальных уравнений. В этом методе краевые условия используются в начальной стадии решения, что во многих случаях исключает необходимость определения произвольных постоянных.
Преобразование Лапласа функции f (x) , обозначаемое символом L(u) , сводится к операции умножения f (x) на e−u x с последующим интегрированием
в интервале от 0 до ∞
∞ |
|
L(u) = ∫e−u x f (x) dx . |
(2.70) |
0 |
|
Величина u может быть действительной и мнимой; в обоих случаях ее действительная часть должна быть достаточно велика, чтобы обеспечить сходимость интеграла.
Выражение L(u) называется изображением оригинала, т.е. функции f (x) . Таким образом, изображения различных функций f (x) могут быть получены непосредственным интегрированием. Например, если f (x) = 
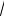x , то изображение этой функции будет
154 |
Часть 2 |
|
|
∞ |
|
|
π |
|
|
|
|
|
|
|
L(u) = ∫e−u x f (x) dx = |
|
. |
|
|
(2.71) |
|||||
4 |
3 |
|||||||||
0 |
|
u |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Обратное изображение дает начальную функцию. Например, |
x называется |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
π |
|
|
||||
исходной функцией, или оригиналом изображения |
|
|
|
. |
|
|
||||
|
|
4 u3 |
|
|
||||||
Преобразования Лапласа первой и второй производных функций |
f (x) оп- |
||||||||||
ределяются соотношениями: |
|
|
|
|
|
|
|
|
|||
|
|
|
|
df |
|
|
|
|
|||
|
|
|
L |
|
|
|
= u L(u) − f (0); |
|
(2.72) |
||
|
|
|
|
|
|||||||
|
|
|
|
dx |
|
|
|
|
|||
d2 |
f |
|
|
|
|
|
d |
|
|
||
L |
|
|
|
= u2 |
L(u) − u f (0) − |
|
f (0). |
(2.73) |
|||
|
2 |
dx |
|||||||||
dx |
|
|
|
|
|
|
|
|
|
||
В этих изображениях f (0) и ее производная представляют граничные усло-
вия, которым должна удовлетворять функция f (x) .
Аналитическое решение большинства задач нестационарной теплопроводности затруднено, поэтому широко используются численные методы решения, которые получили свое развитие при использовании компьютеров.
Численный метод. В основу численного метода определения распределения температуры положено уравнение теплопроводности в конечных разностях, с помощью которого вычисляют температуру в фиксированных точках тела. Для применения численного метода рассматриваемое тело разбивают на ряд элементарных объемов, и центральным точкам каждого объема присваивается номер [15, 20].
Предполагается, что тепловые свойства каждого такого объема сосредоточены в его центральной узловой точке и что передача теплоты между узловыми точками осуществляется через условные теплопроводящие стержни.
Внестационарном состоянии в каждом элементарном объеме подвод и отвод теплоты сопровождается изменением внутренней энергии, причем величина этого изменения зависит от изменения температуры в элементарном объеме в течение рассматриваемого промежутка времени, его теплоемкости, плотности и массы.
Вслучае одномерного нестационарного температурного поля уравнение те-
плопроводности |
∂t |
= a |
d2t |
заменяется уравнением в конечных разностях |
|
||||
|
|
|
|||||||
∂τ |
dx2 |
|
|||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
t |
= a |
2t |
. |
(2.74) |
|
|
|
|
|
Δτ |
|
|||
|
|
|
|
|
|
x2 |
|
||
Решение уравнения (2.74) может быть выполнено аналитически и графически.
Теплопередача в технологических процессах… |
155 |
|
|
Рассмотрим применение численного метода к расчету распределения температуры в плоской стенке. Разобьем стенку на элементарные объемы V = δ·δ·1 = δ2 (рисунок 2.4 а, б), где δ – сторона элементарного объема.
а |
б |
Рис. 2.4. Разбиение и числовая сетка определения нестационарного температурного поля:
а – одномерное температурное поле; б – двухмерное температурное поле
Плотность теплового потока к узловой точке в соответствии с законом Фурье
∂t
равна q = –λ ∂n . При малой величине δ плотность теплового потока можно выразить через конечные разности
q = − |
λ |
t, |
(2.75) |
δ |
|||
|
|
|
где t – разность температур между смежными узловыми точками.
Общее количество теплоты, подведенное к узлу за время Δτ равно
Q = q τ F = − |
λ |
t τ F. |
(2.76) |
|
δ |
|
|
Изменение внутренней энергии в данной узловой точке за время Δτ определяется следующим образом
U = cp ρ V (t′ − t), |
(2.77) |
где t – температура в рассматриваемой узловой точке в момент времени τ; t′ – температура в той же точке в момент времени τ + τ ; V – объем элементарного участка.
Уравнение теплового баланса в конечных разностях для узловой точки 1 (рисунок 2.4а) можно записать в виде
156 |
Часть 2 |
|
|
|
|
Q + Q |
= |
cр ρ V |
(t − t′) . |
|
|
(2.78) |
||||||
|
|
|
|
|
||||||||||
|
|
21 |
31 |
|
τ |
1 |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
С учетом (2.76) уравнение (2.78) принимает вид |
|
|
|
|
|||||||||
|
|
λ (t2 − t1) δ 1+ |
λ |
(t3 − t1) δ 1= |
cрρ V |
|
(t1′ − t1). |
|
(2.79) |
|||||
|
|
δ |
τ |
|
||||||||||
|
|
δ |
|
|
|
|
|
|
|
|
||||
|
Разделим уравнение (2.79) на |
λ и, с учетом того, что V = δ2 1 |
λ |
|
= а |
|||||||||
|
cр ρ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
а τ |
= Fо – критерий Фурье |
(безразмерное |
время), |
искомая температура |
|||||||||
δ2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в рассматриваемой точке 1 в последующий интервал времени τ + τ будет равна
|
′ |
= Fо |
|
|
|
+ t |
|
+ t |
|
1 |
− 2 |
|
. |
(2.80) |
t |
|
|
t |
2 |
3 |
|
|
|
||||||
|
|
|||||||||||||
1 |
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Fо |
|
|
|
|
|
В случае двухмерного температурного поля тело разбивается на элементарные объемы с размерами ячеек x = y = δ . Расчетная схема узловых точек показана на рисунке 2.4б.
В соответствии с рисунком 2.4б искомое уравнение температуры для точки 5 запишется в виде
t′ |
= Fо |
t |
+ t |
|
+ t |
|
+ t |
|
+ t |
|
|
|
1 |
− 4 |
. |
(2.81) |
|
2 |
3 |
4 |
5 |
|
|
||||||||||||
5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Fо |
|
|
|
|
Уравнения (2.80) и (2.81) являются основой численного метода расчета нестационарной теплопроводности одномерного и двухмерного тела.
В качестве примера рассмотрим расчет нестационарной теплопроводности одномерного тела методом разделения переменных.
Охлаждение (нагрев) плоской неограниченной пластины
Рассмотрим неограниченную пластину толщиной 2δ, имеющую в начальный момент времени (τ = 0) постоянную по сечению температуру t0 и помещенную в среду с постоянной температурой tж < t0
Коэффициент теплоотдачи α с обеих сторон стенки одинаков и не изменяется в процессе охлаждения. Известны плотность ρ, теплоемкость cp и коэффициент теплопроводности материала стенки λ. В связи с тем, что линейные размеры поверхности стенки велики по сравнению с ее толщиной, изменение температуры будет происходить только в направлении, перпендикулярном к поверхности стенки.
Таким образом, температурное поле будет одномерным. Кроме того, вследствие симметрии краевых условий относительно середины стенки, температурное поле в любой момент времени будет также симметричным.
Теплопередача в технологических процессах… |
157 |
|
|
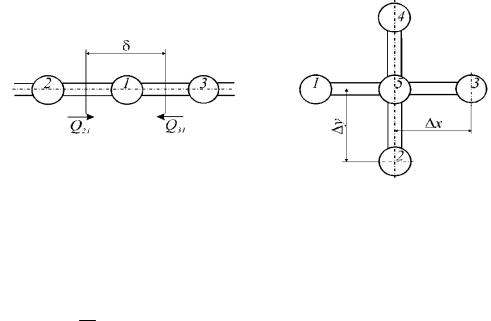
В этом случае удобно выбрать за начало координат точку, лежащую посредине между ограничивающими плоскостями пластины, и направить ось х перпендикулярно к поверхности стенки (рисунок 2.5).
Дифференциальное уравнение теплопроводности для рассматриваемого случая имеет вид:
∂θ |
= а |
∂2θ |
∂θ |
|
|
|
α |
|
|
|
|
||||||
∂τ |
∂x2 ; |
∂x |
|
x=±δ |
= − |
λ |
θx=±δ , (2.82) |
|
|
|
|
|
|
где θ = (t – tж) – избыточная температура. Решая (2.82) методом разделения переменных частное решение первого урав-
нения представим в виде
Рис. 2.5. К решению задачи об охлаждении плоской стенки
θ = С P( )e−а m2 τ . |
(2.83) |
Вид функции P(x) находится из решения уравнения (2.62), которое для одномерного температурного поля записывается следующим образом
2P(x) + m2 P(x) = 0. |
(2.84) |
Это обыкновенное дифференциальное уравнение имеет частное решение в виде функций sin(m x) и cos(m x) .
Отсюда частное решение уравнения (2.83)
θ( ,τ)= A sin( m ) e−a m2 τ + B cos( m ) e−a m2 τ , |
(2.85) |
где m2 – произвольная размерная величина; A и B – произвольные постоянные величины частных решений уравнения теплопроводности.
Из условия симметрии задачи следует, что при x = 0 величина A = 0. Принимая во внимание, что на протяжении всего процесса охлаждения
0 < τ <∞) величина e−a m2 τ |
не равна нулю (m – положительная размерная вели- |
||
чина) частное решение уравнения (2.85) примет вид |
|
||
θ( |
,τ ) = B cos( m |
) e−a m2 τ , |
(2.86) |
а общим решением будет |
|
|
|
|
i=∞ |
) e−a mi2 τ . |
|
θ( ,τ ) = ∑Bi cos( mi |
(2.87) |
||
i=1
158 |
Часть 2 |
|
|
Значения B и m находятся из граничных условий (2.82)
∂θ( ,τ ) = −m B sin( mx) e−a m2τ ,
∂x
и
− m B sin( m δ) e−a m2τ + |
α |
[B cos( m δ) e−a m2τ ]= 0. |
||
|
|
|
λ |
|
Обозначив µ = m δ |
λ |
= Bi |
|
|
и α δ |
|
, |
после ряда преобразований |
|
трансцендентное уравнение для определения , а, следовательно, и m
ctgµ = µ . Bi
(2.88)
(2.88а)
получим
(2.89)
Значения величин Bi (критерий Био) в уравнении (2.87) находим из на-
чальных условий τ = 0, θ(x,0) = θ0 |
|
|
|
|
|
|
|
|
Bi = θ0 |
|
|
2 sinµi |
|
. |
(2.90) |
||
µ |
i |
+ sinµ |
i |
cosµ |
i |
|
||
|
|
|
|
|
||||
Окончательно уравнение распределения температуры в рассматриваемой плоской стенке примет вид
i=∞ |
|
2 sinµi |
|
|
|
x |
|
−µ2 |
Fо |
|
|
|
θ( ,τ ) = θ0 ∑ |
|
µi |
|
e |
. |
(2.91) |
||||||
|
|
cos |
|
|
i |
|
||||||
µi |
+ sinµi cosµi |
|
|
|||||||||
i=1 |
|
|
|
δ |
|
|
|
|
|
|||
Расчеты показывают, что в большинстве случаев существенное влияние на значение вычисляемой температуры оказывает несколько первых членов ряда, а для малых значений критерия Bi <<1 точное решение получается даже при одном члене суммы ряда (2.91).
При x = 0 (середина стенки) имеем
i=∞ |
|
|
2 sinµi |
|
e−µi2 Fо , |
|
||
θс( τ ) = θ0 ∑ |
|
|
|
(2.92) |
||||
µi |
+ sinµi |
cosµi |
||||||
i=1 |
|
|
||||||
при x = ± δ (поверхность стенки) |
|
|
|
|
|
|
|
|
i=∞ |
|
2 sinµi |
cosµi |
e−µi2 Fо . |
|
|||
θп( τ ) = θ0 ∑ |
|
(2.93) |
||||||
|
µi |
+ sinµi cosµi |
||||||
i=1 |
|
|
|
|||||
Из анализа уравнений (2.92) и (2.93) следует, что температуры в центре и на поверхности пластины (θс = tс − tж ; θп = tп − tж ) зависят только от критериев Bi и Fo.
Для проведения расчетов обычно используются графики, которые приводятся в специальной литературе
Теплопередача в технологических процессах… |
159 |
||||
|
|
|
|
|
|
|
θс (τ) |
= f (Fо, Bi) и |
θп (τ) |
= f (Fo,Bi). |
|
|
|
|
|
||
|
θ0 |
θ0 |
|
||
Анализ решений уравнений (2.92) и (2.93) позволяет сделать следующие выводы.
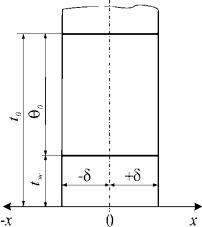
При Bi → ∞ (практически при Bi > 100) температура стенки равна температуре жидкости (рисунок 2.6а), процесс охлаждения определяется свойствами материала стенки (внутренняя задача).
При Bi → 0 (практически при Bi < 0,1) температура по толщине стенки распределяется равномерно (рисунок 2.6б), процесс охлаждения определяется условиями охлаждения стенки (внешняя задача).
При 0,1 < Bi < 100 интенсивность охлаждения стенки зависит как от внут-
реннего сопротивления δ |
, так и от внешнего |
1 |
(рисунок 2.6в). |
λ |
|
α |
|
Рис. 2.6. Распределение температуры в плоской стенке: а – при Bi → ∞; б – при Bi → 0; в – при 0,1 < Bi < 100
Количество теплоты, необходимое для нагревания или охлаждения плоской стенки за время τ с обеих сторон определяется уравнением
Qτ |
= ∫ρ cр (θ0 − θτ ) dV , |
(2.94) |
||
|
|
V |
|
|
а для единичной площади поверхности стенки |
|
|
||
i=∞ |
|
2 sinµi |
(1− e−µi2 Fo ), |
|
Qτ = Q0 ∑ |
|
(2.95) |
||
|
µi2 + µi sinµi cosµi |
|||
i=1 |
|
|
|
|
где Q0 = 2 cp ρ δ θ0 , Дж/м3 – общее количество теплоты за время полного охлаждения стенки.
160 |
Часть 2 |
|
|
2.4. Основные положения конвективного теплообмена
Под конвективным теплообменом понимают процесс передачи теплоты при движении жидкости или газа под влиянием двух процессов – конвекции и теплопроводности.
Конвекцией называется перенос макрочастиц жидкости в пространстве. Если эти частицы перемешаются из области с одной температурой в область с другой температурой, их перемещение сопровождается переносом теплоты. Перенос теплоты конвекцией сопровождается теплопроводностью при непосредственном соприкосновении различно нагретых частиц жидкости.
Количество теплоты, отдаваемое жидкостью твердой стенке или воспринимаемое жидкостью от стенки в единицу времени, определяется уравнением Ньютона – Рихмана
Q = α (t |
с |
− t |
ж |
) F , |
(2.96) |
||||
|
|
|
|
|
|
|
|
||
а плотность теплового потока |
|
|
|
|
|
|
|
|
|
q = α (t |
с |
− t |
ж |
)= α t , |
(2.97) |
||||
|
|
|
|
|
|
|
|
||
где α – коэффициент теплоотдачи, Вт/(м2·К); характеризующий интенсивность конвективного теплообмена между жидкостью и поверхностью твердого тела;
t= tс − tж – температурный напор, K.
Всоответствии с формулой (2.97) по своему физическому смыслу коэффициент теплоотдачи есть плотность теплового потока q на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды. Коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре, равном единице.
Коэффициент теплоотдачи зависит от многих факторов и в общем случае является функцией формы и размера тела, режима движения жидкости, физических свойств жидкости, положения в пространстве и состояния поверхности теплообмена и других величин.
Процесс теплоотдачи в зависимости от природы движения жидкости протекает различно.
Различают вынужденную и свободную конвекцию. В первом случае жидкость или газ движутся за счет внешних для данного процесса сил (насос, вентилятор, ветер), во втором случае – за счет разности плотностей нагретых и холодных частиц жидкости. Возникновение и интенсивность свободного или естественного движения всецело определяется тепловыми условиями процесса и зависят от рода жидко-
сти, разности температур, формы и размеров тела и объема пространства, в котором протекает процесс.
Свободное движение может появиться в жидкости (газе) с переменной плотностью, очевидно, только в том случае, когда жидкость находится в поле земного притяжения.