Иродов И.Е. Общая физика (5 т.) / Иродов. т1 Механика. Основные законы_2014, 12-е изд, 309с

Вязкость

Всем реальным жидкостям в той или иной степени присуще внутреннее трение, или вязкость. Рассмотрим движение жидкости, скорость v отдельных слоев которой зависит только от поперечной координаты z (рис. 4.20). Обобщение результатов опыта приводит к выводу, что сила трения Fтр, действующая между слоями движущейся жидкости, может быть представлена следующей формулой:

где — коэффициент внутреннего трения, или вязкость, — величина, зависящая от природы и состояния жидкости (например, от температуры); 3v/ 3z — градиент модуля скорости (он характеризует крутизну графика зависимости v от z); S — площадь интересующей нас поверхности раздела между слоями (эта поверхность перпендикулярна оси Z).

Формула (4.78) означает, что жидкость, находящаяся над поверхностью S (рис. 4.20), действу- ет на жидкость под поверхностью S с

силой Fтр (вправо), а нижняя часть

жидкости действует на верхнюю

часть с той же по модулю силой Fтр,

но влево.

Из рис. 4.20 видно, что сила вяз-

Рис. 4.20

кости вдоль поверхности S, проведенной через точку 1, будет меньше,

чем через точку 2, поскольку крутизна графика v(z), а значит, и градиент 3v/ 3z в точке 2 больше.

Приведем значения вязкости для некоторых жидкостей при ком-

Ламинарное и турбулентное течения. Особенностью ламинарного (слоистого) течения является его регулярность. Например, при ламинарном течении в прямолинейной трубе частицы жидкости движутся вдоль прямолинейных траекторий, параллельных оси трубы. Однако при достаточно больших скоростях ламинарное течение становится неустойчивым и переходит в

турбулентное, при котором частицы жидкости совершают нерегулярные беспорядочные движения, что приводит к интенсивному перемешиванию между слоями движущейся жидкости.

Такие быстрые и нерегулярные изменения происходят вследствие неустойчивости ламинарных течений при определенных условиях. Характер течения зависит от значения безразмерной величины — числа Рейнольдса:

где — плотность жидкости, v — характерная скорость потока, l — характерный размер, — вязкость.

При малых значениях числа Re наблюдается ламинарное течение. Но, начиная с некоторого критического значения Re, ламинарное течение переходит в турбулентное. Если в качестве характерного размера, например для круглой трубы, взять ее радиус, то критическое значение Re 6 1000 (для воды).

Течение жидкости в трубе круглого сечения

Пусть вязкая жидкость течет в прямой трубе радиуса R. Течение стационарное, линии тока параллельны оси трубы. Скорость жидкости равна нулю у стенок трубы и максимальна на ее оси. Найдем сначала зависимость скорости жидкости от расстояния до оси, т. е. v (r).

Выделим мысленно цилиндриче-

ский объем жидкости радиуса r и длины l (рис. 4.21). Поскольку все элементы жидкости движутся без ускорения, сумма всех внешних сил, приложенных к любому объему жидкости, равна нулю. На боковую поверхность выделенного цилиндра

действует сила трения, равная | dv/dr | 2 rl. На основания

этого цилиндра — силы давления, алгебраическая сумма которых равна ( p1 p2 ) r 2 .

Течение стационарное, поэтому эти две взаимно противоположные силы должны быть равны по модулю друг другу:

4.2.Консервативность сил поля. Имеются два стационарных силовых поля: 1) F = аyi; 2) F = аxi + byj, где i, j — орты осей X и Y; a и b

— постоянные.

Консервативны ли силы этих полей?

Р е ш е н и е. Найдем работу силы каждого поля на пути от некоторой точки 1(x1, y1) до некоторой точки 2(x2, y2):

В первом случае интеграл зависит от вида функции y(x), т. е. от пути, поэтому первая сила неконсервативная. Во втором случае оба интеграла не зависят от пути, они зависят только от координат начальной и конечной точек пути. Следовательно, вторая сила консервативная.

4.3. Потенциальная энергия частицы в поле. Сила, действующая на частицу в некотором поле консервативных сил, имеет вид F a( yi xj), где a — постоянная, i и j — орты осей X и Y. Найти

потенциальную энергию U(x,y) частицы в этом поле.

Р е ш е н и е. Вычислим элементарную работу силы F на перемещении dr и представим ее, согласно (4.14), в виде убыли некоторой функции U. Эта функция и есть, по определению, потенциальная энергия частицы в данном поле. Итак,

A F dr a( y dx x dy) d ( axy).

Отсюда U( x, y) axy const.

4.4.О разных подходах к решению. Шарик массы m подвесили на упругой невесомой нити, жесткость которой k. Затем шарик подняли так, чтобы нить оказалась в недеформированном состоянии,

и без толчка отпустили. Найти максимальное удлинение xm нити в процессе движения шарика.

Р е ш е н и е. Рассмотрим три эквивалентных способа решения, основанных на энергетических соображениях.

1. Исходим из уравнения (4.29): приращение кинетической энергии шарика должно быть равно алгебраической сумме работ всех сил, действующих на него. В нашем случае это сила тяжести mg и упругая сила со стороны нити Fупр = kx, где x — удлинение нити. В начальном и конечном положениях шарика его кинетическая энергия равна нулю (ясно, что при максимальном растяжении нити шарик остановится), поэтому, согласно (4.29), сумма работ

Aтяж + Aупр = 0, или

x m

mgxm ( kx )dx mgxm kxm2 /2 0.

0

Отсюда xm = 2mg/k.

2. Можно рассматривать шарик в поле тяжести Земли. При таком подходе следует говорить о полной механической энергии шарика в поле тяжести Земли. Приращение этой энергии, согласно (4.31), равно работе сторонних сил. В данном случае сторонней силой надо считать силу упругости, приращение же полной механической энергии шарика равно приращению только его потенциальной энергии в поле тяжести Земли. Поэтому

x m

E 0 mgxm ( kx )dx kxm2 /2.

0

Отсюда тот же результат для xm.

Заметим, что можно было бы поступить и наоборот, т. е. рассматривать шарик в поле упругой силы. Тогда роль сторонней силы играла бы сила тяжести. Полезно убедиться, что и в этом случае результат будет тем же.

3. И наконец, можно рассматривать шарик в поле, образованном совместным действием и силы тяжести, и упругой силы. Тогда сторонние силы отсутствуют и полная механическая энергия шарика в таком поле остается постоянной в процессе движения, т. е.E K U 0. При переходе шарика из начального положе-

Результат опять тот же.

4.5.Небольшое тело массы m поднимается с нулевой начальной скоростью с поверхности земли под действием двух сил: силы F, меняющейся с высотой подъема y по закону F 2mg(1 ay), где a —

положительная постоянная, и силы тяжести mg. Найти работу силы F на первой половине пути подъема и соответствующее приращение потенциальной энергии тела в поле тяжести Земли. Поле тяжести предполагается однородным.

Р е ш е н и е. Сначала найдем весь путь подъема. В начале и кон-

це пути скорость тела равна нулю, поэтому равно нулю и приращение кинетической энергии тела. Согласно (4.29), K равно алгебраической сумме работ А силы F и силы тяжести. А так какK 0, то и А = 0. Учитывая, что положительное направление

оси Y взято вверх, запишем

Отсюда h = 1/a.

Работа силы F на первой половине пути подъема

h / 2 h / 2

AF Fy dy 2mg (1 ay) dy 3mg /4a.

00

Соответствующее приращение потенциальной энергии

U mgh/2 mg /2a.

4.6.Потенциал и напряженность поля. Найти потенциал и напряженность гравитационного поля, созданного однородным шаром массы M и радиуса R, в зависимости от расстояния r до его центра.

Р е ш е н и е. Сначала определим потенциал поля, создаваемого тонким однородным сферическим слоем вещества массы m и радиуса a. Для этого найдем потенциал d в точке P (r a ), который создает элементарный пояс dS данного слоя (рис. 4.24, a). Если масса этого пояса dm и его точки находятся на расстоянии x

Рис. 4.24

от точки P, то d dm/x. Учитывая, что dm 1/2 m sin d , получаем

Преобразуем (1) с помощью (2) к виду d 1/2 ( m/ar ) dx и проинтегрируем это уравнение по всему слою. Тогда

Таким образом, потенциал в точке P вне тонкого однородного сферического слоя таков, как если бы вся масса этого слоя была сосредоточена в его центре. Если же точка P находится внутри слоя (r < a), то предыдущие расчеты остаются в силе вплоть до интегрирования. Теперь пределы интегрирования по x будут от a – r до a + r. В результате

т. е. потенциал внутри слоя не зависит от положения точки P, а следовательно, он одинаков во всех точках внутри слоя.

Напряженность поля в точке P, согласно (4.26),

4.7.Космические скорости. Показать, что кинетическая энергия K2, которую необходимо сообщить телу для удаления его за пределы

земного тяготения, в два раза превышает кинетическую энергию

K1, необходимую для выведения этого тела на круговую орбиту искусственного спутника Земли (вблизи ее поверхности). Сопро-

тивлением воздуха и вращением Земли пренебречь.

Р е ш е н и е. Найдем скорость v1 тела, движущегося по круговой орбите. Согласно основному уравнению динамики,

mv12 /R mg ,

где m — масса тела, R — радиус орбиты, приблизительно равный радиусу Земли. Отсюда

v1 gR 7,9 км/с.

Это первая космическая скорость.

Для того чтобы тело могло преодолеть поле тяготения Земли, ему необходимо сообщить вторую космическую скорость v2. Ее можно найти из закона сохранения энергии: кинетическая энергия тела вблизи поверхности Земли должна быть равна глубине потенциальной ямы в этом месте. Последняя равна приращению потенциальной энергии тела в поле тяготения Земли между точками r1 = R и r2 = %. Таким образом,

mv22 /2 mM /R ,

где M — масса Земли. Отсюда

v2 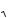2 M /R 2gR 11 км/ с.

Следовательно, v2 v1 2 и K2 = 2K1.

4.8.Решение в неинерциальной системе отсчета. Плоскую жесткую спираль из гладкой проволоки, расположенную в горизонтальной плоскости, вращают с постоянной угловой