
Иродов И.Е. Общая физика (5 т.) / Иродов. т1 Механика. Основные законы_2014, 12-е изд, 309с
.pdf
210 |
Глава 6 |
|
|
Рис. 6.12
б) = , тогда y = –(b/а)х и частица движется тоже по прямой, но во втором и четвертом квадрантах (рис. 6.12, б);
в) = /2. В этом случае х2/а2+y2/b2 =1, т. е. частица движется по эллипсу, полуоси которого а и b совпадают с осями координат. При а = b эллипс превращается в окружность. Так как колебания вдоль оси Y происходят с опережением по фазе на /2 относительно колебаний по оси Х, то сначала y и лишь затем х достигают максимальных значений. Это значит, что движение частицы будет происходить по часовой стрелке (рис. 6.12, в);
г) = 3 /2. Это то же, что и = – /2, поскольку изменение фазы на 2 несущественно (рис. 6.12, г).
Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории результирующего движения имеют более сложные формы. Их называют фигура-
ми Лиссажу. Одна из этих фигур показана на рис. 6.13, она соответствует отношению частот y : x 3 : 2.
Рис. 6.13 |
|
|
|
|
|
И последнее: при сложении взаимно пер- |
||||||||||||||
|
|
|
|
пендикулярных колебаний полная энергия |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
& |
k |
1 x |
2 |
|
k 2 y |
2 |
) |
|
m |
|
|
|
|
|
|
|
|
|
E |
|
( |
|
|
|
+ |
|
2 |
|
2 |
) |
|
Ex |
|
Ey , |
(6.24) |
||||
( |
|
|
|
|
|
+ |
|
|
||||||||||||
|
|
2 |
|
2 |
|
2 |
(x |
y |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т. е. складывается из энергий каждого колебания (в отличие от сложения колебаний одного направления). Согласно (6.13), эта энергия
E m (a2 |
2 |
b |
2 2 ). |
(6.25) |
2 |
x |
|
y |
|

Колебания |
211 |
|
|
§ 6.3. Затухающие колебания
Уравнение затухающих колебаний
В любой реальной колебательной системе есть силы сопротивления (трения), действие которых приводит к уменьшению амплитуды и энергии колебаний. Такие свободные колебания называют затухающими.
Будем исходить из основного уравнения динамики, полагая, что на частицу массы m действует кроме квазиупругой силы (–kx) сила сопротивления, пропорциональная скорости частицы, Fx rx, где r — коэффициент сопротивления (величина размерная). Тогда уравнение движения будет иметь вид
|
|
|
|
(6.26) |
|
mx |
–kx rx, |
||
или |
|
|
|
|
|
|
|
2 |
(6.27) |
|
x 2 |
x 0 x 0, |
||
где 2 r/m, 20 k/m. Отметим, что 0 — это частота свободных колебаний без трения. Частоту 0 называют собственной частотой осциллятора, а — коэффициентом затухания.
Уравнение (6.27) при условии 0 описывает затухающие колебания. Его решение имеет вид
x a 0 e t cos ( t ), |
(6.28) |
где а0 и — постоянные, определяемые начальными условиями x (0) = x0 и x (0) x0 , — частота затухающих колебаний:
|
|
|
|
20 2 . |
(6.29) |
||
|
|
|
|
.График функции (6.28) показан на рис. 6.14 для случая x0 0
иx0 0. Видно, что эта функция не периодическая. Тем не менее величину T = 2 / принято называть периодом затухающих
колебаний:
T 2 / 20 2 . |
(6.30) |
Множитель a a 0 e t перед косинусом в (6.28) называют
амплитудой затухающих колебаний (пунктир на рис. 6.14).
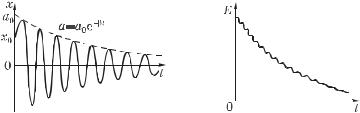
212 |
Глава 6 |
|
|
Рис. 6.14 |
Рис. 6.15 |
Энергия затухающих колебаний
Эта энергия складывается из потенциальной и кинетической: E kx2/2 mx2 /2. После подстановки сюда выражений х (t) и x (t), соответствующих затухающими колебаниям (6.28), получим зависимость E(t), которая графически показана на рис. 6.15. Уменьшение энергии колебаний обусловлено работой силы сопротивления. Мощность этой силы равна rx , x rx2 , тогда
dE/dt rx2 .
Таким образом, dE/dt 0, кроме тех моментов, когда x 0. При малом затухании ( 0) зависимость E(t) становится
практически экспоненциальной:
E E0 e 2 t . |
(6.31) |
Отсюда убыль энергии в единицу времени |
|
dE/dt 2 E. |
(6.31*) |
Характеристики затухания
Кроме коэффициента затухание характеризуют и другими величинами:
1. Время релаксации — это время, за которое амплитуда колебаний уменьшается в е раз. Из выражения a a 0 e t видно, что
1/ . |
(6.32) |
2. Логарифмический декремент затухания. Его определяют как

Колебания |
|
|
213 |
|
|
|
|
: ln |
a (t ) |
T, |
(6.33) |
|
|||
|
a (t + T )
где Т — период затухающих колебаний. Из предыдущих двух формул следует, что
: 1/ N e , |
(6.34) |
где Ne — число колебаний за время , в течение которого амплитуда уменьшается в е раз.
При малом затухании ( 0) : характеризует относительное уменьшение амплитуды колебаний за период. Это следует из (6.33), поскольку в этом случае
|
a a |
& |
a ) |
6 |
a |
|
|
|
: ln |
|
ln (1 + |
|
+ |
|
. |
(6.35) |
|
|
|
|
||||||
|
a |
|
a |
|
a |
|
|
|
Кроме того, при 0 относительное уменьшение энергии колебаний за период, согласно (6.31*), равно E/ E 2 T 2:, откуда
: E/2E. |
(6.36) |
3. Добротность осциллятора. По определению, |
|
Q / : Ne . |
(6.37) |
При малом затухании ( 0), когда справедливо (6.36),
Q 6 2 E/ E. |
(6.38) |
Пример. Найдем добротность осциллятора, у которого амплитуда смещения уменьшается в раз через каждые N колебаний.
Поскольку Q /: ! T, задача сводится к определению
и Т. Пусть t — время, за которое амплитуда уменьшается враз, тогда e t и t ln . Кроме того, T t/N. После
подстановки выражений для и Т в исходную формулу получим Q N/ln .
В заключение отметим, что при достаточно большом затухании ( j 0) система совершает апериодическое движение: вы-

214 |
Глава 6 |
|
|
веденная из положения равновесия, она возвращается в это положение, не совершая колебаний.
§ 6.4. Вынужденные колебания
Уравнение вынужденных колебаний
Свободные колебания реальной колебательной системы являются, как мы выяснили, затухающими. Чтобы возбудить в такой системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные силами сопротивления (трения). Это можно осуществить, воздействуя на систему переменной внешней силой F, изменяющейся — в простейшем и практически наиболее важном случае — по гармоническому закону Fx Fm cos t. Возникающие при этом колебания и называют вынужденными.
Теперь на колеблющуюся частицу будут действовать одновременно три силы: квазиупругая (–kx), сила сопротивления ( rx) и внешняя, вынуждающая (Fx). Согласно основному уравнению динамики,
|
|
|
|
|
|
Fm cos t, |
(6.39) |
|
|
|
mx –kx |
rx |
|||||
или в более удобной форме |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
fm cos t, |
(6.40) |
|
|
|
x |
2 x 0 x |
|||||
где 2 r/m, 2 |
k/m, f |
m |
F |
m |
/m. |
|
||
0 |
|
|
|
|
|
|
||
Опыт показывает, что по истечении некоторого времени (с момента начала действия вынуждающей силы) в системе устанавливаются гармонические колебания* с частотой вынуждаю-
щей силы, но отстающие по фазе от последней на : |
|
x a cos ( t ). |
(6.41) |
*Решение уравнения (6.40), как доказывается в математике, представляет собой сумму общего решения однородного уравнения (когда правая часть равна
нулю) и частного решения неоднородного:t cos ( t ) a cos ( t ).x a 0 e
Нас будет интересовать только частное решение, соответствующее установившимся колебаниям. Общее решение однородного уравнения описывает затухающие колебания, которые по истечении некоторого времени практически исчезают.

Колебания |
215 |
|
|
Наша задача — определить постоянные а и . Для этого продифференцируем (6.41) дважды по времени:
x a sin ( t ) a cos ( t /2), |
|||||
|
|
|
|
|
|
|
2 |
2 |
|
(6.42) |
|
x a cos ( t ) a |
|
cos ( t ) |
|||
и подставим выражения для |
|
и |
|
||
х, x |
x в исходное уравнение |
||||
(6.40). Сумма трех гармонических функций в левой части
(6.40) должна быть равной функ-
ции fm cos t. Учитывая фазовые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сдвиги между х, x |
и x, предста- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вим это равенство с помощью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
векторной диаграммы (рис. 6.16, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
для случая 0 ). В скобках на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
этой диаграмме указаны «проис- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
хождения» |
(или |
соответствие) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
векторов, модули которых имеют |
Рис. 6.16 |
|
|||||||||||||||||
размерность ускорения. Из этой |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
диаграммы |
по |
теореме |
Пифагора |
|
|
|
|
следует, |
что |
||||||||||
a2 ( 2 2 )2 |
4 2 2 a2 f 2 , откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a fm / ( 20 |
2 )2 4 2 2 . |
|
|
|
|
|
|
|
|
|
(6.43) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этой диаграммы видно, что отставание смещения по фазе
на от вынуждающей силы определяется как |
|
tg 2 /( 20 2 ). |
(6.44) |
Формулы (6.43) и (6.44) показывают, что амплитуда а колебаний и отставание смещения по фазе на от вынуждающей силы определяются свойствами самого осциллятора ( 0 , ) и вынуждающей силы (fm, ), но не начальными условиями.
Резонанс
На рис. 6.17 приведены графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы а( ) для трех коэффициентов затухания. Видно, что а( ) имеет максимум при частоте, которую легко найти из условия da/d 0 (до-

216 Глава 6
статочно найти экстремум подкоренного выражения). Эту частоту называют
резонансной:
|
|
|
|
|
|
|
|
рез |
2 |
2 2 , |
(6.45) |
||
|
0 |
|
|
|
||
|
|
|
|
|
|
|
а существование максимума амплитуды а — явлением резонанса. Соответ-
Рис. 6.17 |
ственно приведенные на рис. 6.17 гра- |
|
|
фики принято называть резонансными кривыми. |
|
Выражение для амплитуды при резонансе получим, подста-
вив (6.45) в (6.43): |
|
|
|
|
|
|
|
a |
макс |
|
fm |
|
|
. |
(6.46) |
|
|
|
|
||||
2 2 |
|
||||||
|
|
2 |
|
||||
|
|
0 |
|
|
|
|
|
Чем меньше затухание системы, тем более ярко выражен резонанс. Явление резонанса играет огромную роль в физике и технике. Его используют, если нужно усилить колебания, и, наоборот, всячески избегают, если резонанс может привести к нежелательным усилениям колебаний.
Зависимость фазового сдвига от частоты показана на рис. 6.18 (для двух коэффициентов затухания). При слабом затухании рез 6 0 , и значение при резонансе практически равно /2 (см. рис. 6.16).
На рис. 6.19 дан график зависимости средней (за период) мощности вынуждающей силы от ее частоты pP( )q. Заметим, что pP( )q max при 0 независимо от коэффициента зату-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.18 |
|
|
|
|
|
|
|
|
|
|
Рис. 6.19 |
|||||||||||||||||||||||||||

Колебания |
217 |
|
|
хания . Важным параметром резонансной кривой pP( )q, характеризующим «остроту» резонанса, является ее ширина на половине «высоты». Можно показать, что при малом затухании ( 0) «острота» резонанса, т. е. отношение 0 / , равно добротности осциллятора:
0 / Q. |
(6.47) |
Энергия вынужденных колебаний
Интересно проследить, как зависит энергия E осциллятора, совершающего установившиеся колебания, от времени. Так как E = U + K, то
2 |
/2 |
|
2 |
/2 |
|
|
E = kx |
|
mx |
|
|
||
ma2 [ 20 cos2 ( t ) 2 sin2 ( t )]/2, |
(6.48) |
|||||
где учтено, что k m 2 . График зависимости E(t) для случая |
||||||||||||||||||||||||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
показан |
на рис. 6.20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Колебания энергии E будут тем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
меньше, чем ближе частота к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0, и при 0 |
энергия E не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
будет |
зависеть |
от времени t: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E |
0 |
ma2 2 /2 const. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
установившихся колеба- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ниях при 0 |
работа вынуж- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дающей силы за период будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
компенсировать |
потери энер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
гии в системе за счет работы |
|
|
|
|
|
|
|
|
|
|
Рис. 6.20 |
|||||||||||||||||||||
сил сопротивления. Мощность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
же вынуждающей силы в каждый момент будет равна модулю мощности сил сопротивления только в случае 0 . В противном случае эти мощности будут равны по модулю только в среднем за период.
Пример. Найдем среднюю за период мощность pPq вынуждающей силы, необходимую для поддержания среднего значения кинетической энергии на уровне pKq у осциллятора с коэффициентом затухания .

218 |
Глава 6 |
|
|
Согласно закону сохранения энергии, pPq должно быть равно модулю среднего значения мощности силы сопротивления:
pPq |p r x , xq| prx 2 q.
Так как x 2 2K /m, то r x 2 2(r /m )K 4 K и pPq 4 pKq.
Задачи
6.1.Свободные колебания без трения. Идеальная жидкость объемом V
налита в U-образную трубку (рис. 6.21) с площадью поперечного
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сечения канала S. Найти период малых колебаний |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жидкости. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е. Эту задачу наиболее просто решать с |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
помощью дуговой координаты l. Проецируя все |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы, действующие на жидкость, на орт t, полу- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чим, |
согласно основному |
уравнению динамики |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m l |
F (2.16), m l gS , 2l, где справа записана |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проекция единственной |
некомпенсированной |
|||
|
|
|
|
|
Рис. 6.21 |
силы — силы тяжести, действующей справа на |
|||||||||||||||||||
|
|
|
|
|
элемент жидкости длины 2l. Отсюда, имея в виду, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что m/ V , получаем |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l (2gS/V ) l 0. |
|
||
Значит, 2 |
2gS/V и T |
|
. |
|
|||||||||||||||||||||
2V /gS |
|
||||||||||||||||||||||||
0 |
|
|
|
|
|
||||||||||||||||||||
6.2. Крутильные колебания. Горизонтальный диск с моментом инер-
|
|
|
|
|
|
|
|
|
|
|
ции I относительно его оси укреплен в центре |
|
|
|
|
|
|
|
|
|
|
|
тонкого упругого стержня (рис. 6.22). При пово- |
|
|
|
|
|
|
|
|
|
|
|
роте диска на него действует момент упругих |
|
|
|
|
|
|
|
|
|
|
|
сил M z D , где D — коэффициент кручения. |
|
|
|
|
|
|
|
|
|
|
|
Найти частоту 0 и амплитуду m крутильных |
|
|
|
|
|
|
|
|
|
|
|
колебаний, если в начальный момент диск по- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вернули на угол 0 из положения равновесия и |
|
|
|
Рис. 6.22 |
сообщили ему угловую скорость 0 . |
|||||||
Р |
е ш е н |
и е. Из уравнения движения I D находим |
|||||||||
0 |
|
|
D/I |
. Амплитуду колебаний проще всего найти из того, что |
|||||||
энергия колебаний (E = U + K) здесь будет сохраняться. Значит, энергия в начальный момент будет равна энергии при максимальном отклонении из положения равновесия:
D 20 /2 I 20 /2 D 2m /2.

Колебания |
219 |
|
|
Отсюда m 
 20 ( I /D ) 20 .
20 ( I /D ) 20 .
Заметим, что выражение для потенциальной энергии (U D 2 /2)
следует из ее определения, а именно: убыль величины U равна работе упругой силы (в данном случае ее момента):
U(0) U( ) M z d.
0
В положении равновесия ( = 0) полагаем U(0) = 0.
6.3.Физический маятник. На каком расстоянии х от центра С надо подвесить тонкий однородный стержень длины l, чтобы период его малых колебаний был наименьшим?
Р е ш е н и е. Согласно (6.10), период колебаний физического маятника T 2 
 I /mgx , где I — момент инерции стержня относи-
I /mgx , где I — момент инерции стержня относи-
тельно |
искомой точки подвеса. По теореме Штейнера, |
|||
I |
I |
C |
mx |
2 , где I — момент инерции относительно центра масс |
|
|
|
C |
|
С. Подставив это выражение в формулу для Т, получим
T 2 
 (l /12x x/l ) l /g .
(l /12x x/l ) l /g .
Период Т будет наименьшим при условии dT/dх = 0 (или при равенстве нулю производной от подкоренного выражения):
l /12x 2 1/l 0,
откуда x l /
 12.
12.
6.4.Однородный стержень положили на два быстро вращающихся блока (рис. 6.23). Известны расстоя-
ние l между осями блоков и коэффициент трения k между стержнем и блоками. Показать, что стержень будет совершать гармонические колебания. Найти их период.
Рис. 6.23
Р е ш е н и е. Согласно основному уравнению динамики,
|
F1 |
F2 |
k ( R1 R 2 ). |
(*) |
mx |
