Иродов И.Е. Общая физика (5 т.) / Иродов. т1 Механика. Основные законы_2014, 12-е изд, 309с

где Асп — работа сил поля, Астор — работа сторонних сил. Согласно (4.10), работа сил поля равна убыли потенциальной

энергии частицы: A сп U. Подставив это выражение в предыдущее и перенеся U влево, получим

K U (K U) A стор .

Отсюда видно, что работа сторонних сил идет на приращение K + U. Эту величину — сумму кинетической и потенциальной энергий — называют полной механической энергией частицы в поле и обозначают E:

Заметим, что полная механическая энергия E, как и потенциальная U, определяется с точностью до произвольной постоянной.

Итак, из предыдущих двух уравнений следует, что приращение полной механической энергии частицы в стационарном поле консервативных сил при перемещении ее из точки 1 в точку 2 можно записать в виде

т. е. приращение полной механической энергии частицы на некотором пути равно алгебраической сумме работ всех сторонних сил, действующих на частицу на том же пути. Если

A стор 0, то полная механическая энергия частицы увеличивается, если A стор 0, то уменьшается.

Пример. Тело массы m бросили со скоростью v0 с обрыва высотой h над поверхностью воды. Найдем работу, которую совершила сила сопротивления со стороны воздуха, при условии, что тело упало на поверхность воды со скоростью v.

Если рассматривать движение тела в поле сил тяжести, то сила сопротивления со стороны воздуха будет сторонней и, согласно уравнению (4.31), искомая работа Aстор E2 E1mv 2 /2 (mv02 /2 mgh ) или

Aстор m(v 2 v02 )/2 mgh.

Интересно, что полученная величина может оказаться не только отрицательной, но и положительной (это зависит, например, от характера ветра в процессе падения тела).

Итак, полная механическая энергия частицы может измениться под действием только сторонних сил. Отсюда непосредственно вытекает закон сохранения механической энергии частицы: если сторонние силы отсутствуют или таковы, что не совершают работы в течение интересующего нас времени, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной за это время:

Уже в такой простейшей форме закон сохранения энергии позволяет достаточно легко получать ответы на ряд важных вопросов без привлечения уравнений движения, что часто сопряжено с проведением громоздких и утомительных расчетов. Именно это обстоятельство и превращает законы сохранения в весьма действенный инструмент исследования.

Проиллюстрируем возможности и преимущества, которые дает применение закона сохранения (4.32), на следующем примере.

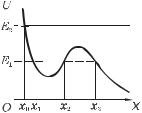
Пример. Пусть частица движется в одномерном стационарном поле, где ее потенциальная энергия U(х)

имеет вид, как на рис. 4.9. Если сторонние силы отсутствуют, то полная механическая энергия час-

тицы в данном поле, т. е. E, не изменяется в процессе движения и можно просто ответить, например, на следующие вопросы.

1. Определить, не решая основного уравнения динамики, скорость частицы в зависимости от ее координаты.

Для этого достаточно знать, согласно уравнению (4.32), конкретный вид потенциальной кривой U(х) и значение полной энергии E.

2. Установить область изменения координаты x частицы, в которой она может находиться при данном значении полной энергии E.

Ясно, что в область, где U>E, частица попасть не может, поскольку потенциальная энергия U частицы не должна превышать ее полную энергию. Отсюда сразу следует, что при E = E1 (рис. 4.9) частица будет двигаться или в области между коор-

Учитывая, что F2 F1 (согласно третьему закону Ньютона), перепишем предыдущее уравнение:

A1,2 F1 (dr1 dr2 ).

Величина, стоящая в скобках, представляет собой не что иное, как перемещение частицы 1 относительно частицы 2, точнее, перемещение частицы 1 в K -системе отсчета, жестко связанной с частицей 2 и перемещающейся вместе с ней поступательно относительно исходной K-системы отсчета. Действительно, перемещение dr1 частицы 1 в K-системе отсчета может быть представлено как перемещение dr2 K -системы отсчета (связанной с частицей 2) плюс перемещение dr1 частицы 1 относительно этой K -системы, т. е. dr1 dr2 dr1 . Отсюда dr1 dr2 dr1 и

A1,2 F1 dr1 .

Полученный таким образом результат весьма замечателен: алгебраическая сумма элементарных работ пары сил взаимодействия в произольной K-системе отсчета оказывается всегда равной элементарной работе, которую совершает сила, действующая на одну частицу, в системе отсчета, где другая частица покоится. Иначе говоря, работа А1,2 не зависит от выбора исходной K-системы отсчета.

Сила F1, действующая на частицу 1 со стороны частицы 2, является центральной, а значит и консервативной. Поэтому работа данной силы на перемещении dr1 может быть представлена, согласно (4.10), как убыль потенциальной энергии частицы 1 в поле частицы 2 или как убыль потенциальной энергии взаимодействия рассматриваемой пары частиц:

A1,2 dU1 2 ,

где U12 — функция, зависящая только от расстояния между этими частицами. При конечном же перемещении

A1,2 U1 2 .

Рассмотрим теперь систему из трех частиц. (Полученный в этом случае результат легко обобщить и на систему из произвольного числа частиц.) Работа, которую совершают все силы

взаимодействия при перемещении всех частиц, может быть представлена как алгебраическая сумма работ всех трех пар сил взаимодействий: A A1,2 A1,3 A2,3 . Но для каждой пары этих сил A ik Uik , поэтому

A (U1 2 U1 3 U2 3 ) Uсоб ,

где Uсоб — собственная потенциальная энергия данной системы частиц:

Uсоб U1 2 U1 3 U2 3 .

Так как каждое слагаемое этой суммы зависит от расстояния между соответствующими частицами, то очевидно, что собственная потенциальная энергия данной системы зависит от относительного расположения частиц (в один и тот же момент), или, другими словами, от конфигурации системы.

Подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому каждой конфигурации системы частиц присуще свое значение собственной потенциальной энергии и работа всех внутренних центральных (консервативных) сил при изменении этой конфигурации равна убыли собственной потенциальной энергии системы:

где U1 соб и U2 соб — собственная потенциальная энергия системы в начальном и конечном состояниях.

Таким образом, суммарная работа внутренних центральных сил не зависит от того, как конкретно система переходит от конфигурации 1 к конфигурации 2. Данная работа определяется исключительно самими конфигурациями системы. Все это позволяет дать более общее определение консервативных сил:

консервативными называют силы, зависящие только от конфигурации системы и суммарная работа которых не зависит от «пути» перехода, а определяется только начальной и конечной конфигурациями системы.

Собственная потенциальная энергия системы — величина не аддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще

потенциальную энергию взаимодействия Uвз отдельных частей системы:

где Un — собственная потенциальная энергия n-й части системы.

Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до произвольной постоянной.

В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего покажем, что эта энергия может быть представлена в виде

где Ui — потенциальная энергия взаимодействия i-й частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы.

Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная

энергия данной системы Uсоб U1 2 U1 3 U2 3 . Преобразуем эту сумму следующим образом. Представим каждое слагаемое Uik в симмет-

ричном виде: Uik (Uik Uki )/2, так как ясно, что Uik Uki . Тогда

Uсоб 1/2 (U1 2 U2 1 U1 3 U3 1 U2 3 U3 2 ).

Сгруппируем члены с одинаковым первым индексом:

Uсоб 1/2 [(U1 2 U1 3 ) (U2 1 U2 3 ) (U3 1 U3 2 )] .

Каждая сумма в круглых скобках представляет собой потенциальную энергию Ui взаимодействия i-й частицы с остальными двумя. Поэтому последнее выражение можно переписать так:

3

Uсоб 1/2 (U1 U2 U 3 ) 1/2 .Ui , i 1

что полностью соответствует формуле (4.35).

Обобщение полученного результата на произвольную систему очевидно, так как подобные рассуждения не зависят от числа частиц, составляющих систему.

Для системы, взаимодействие между частицами которой имеет гравитационный или кулоновский характер, формулу (4.35) можно преобразовать и к другому виду, воспользовавшись понятием потенциала. Заменим в (4.35) потенциальную энергию i-й частицы выражением Ui mi i , где mi — масса (заряд) i-й частицы, а i — потенциал, создаваемый всеми остальными частицами системы в точке нахождения i-й частицы. Тогда

Если массы (заряды) распределены в системе непрерывно, то суммирование сводится к интегрированию:

где — объемная плотность массы (заряда), dV — элемент объема. Здесь интегрирование проводится по всему объему, занимаемому массами (зарядами).

«Внешняя» потенциальная энергия системы

Рассмотрим случай, когда система находится во внешнем стационарном поле консервативных сил. В этом случае каждая частица системы будет характеризоваться своим значением потенциальной энергии Ui в данном поле, а вся система — величиной

Эту величину мы и будем называть «внешней» потенциальной энергией системы в отличие от Uсоб — собственной потенциальной энергии, зависящей только от взаимодействия частиц системы между собой.

Согласно (4.10), убыль потенциальной энергии каждой частицы во внешнем поле равна работе силы данного поля на соответствующем перемещении, поэтому убыль Uвнеш всей системы равна Авнеш — алгебраической сумме работ всех сил внешнего поля, действующих на все частицы системы:

Получим полезную формулу для вычисления внешней потенциальной энергии системы, находящейся в однородном силовом поле. Пусть, например, это поле тяжести, где на i-ю частицу системы действует сила mig. В этом случае потенциальная энергия данной частицы, согласно (4.13), есть migzi, где zi — вертикальная координата частицы, отсчитанная от некоторого произвольного уровня О. Тогда потенциальная энергия всей системы во внешнем однородном поле (собственная потенциальная энергия нас сейчас не интересует) может быть записана так:

Uвнеш .m i gz i .m i z i g.

Сумма, стоящая в скобках, в соответствии с (3.8) есть не что иное, как произведение массы m всей системы на вертикальную координату zC центра масс данной системы, т. е.

.m i z i mz C . Поэтому выражение для Uвнеш можно переписать в окончательном виде:

т. е. потенциальная энергия системы во внешнем однородном поле тяжести равна произведению массы m системы на g и на вертикальную координату zC ее центра масс.

Приращение величины Uвнеш при перемещении системы рав-

но

где z C — приращение вертикальной координаты центра масс данной системы частиц.

§ 4.5. Закон сохранения механической энергии системы

Диссипативные силы

Помимо разделения всех сил на внешние и внутренние (в зависимости от выбора системы частиц), силы, как мы уже знаем, принято подразделять на консервативные и неконсервативные (в зависимости от их природы).

К неконсервативным силам относятся диссипативные силы — это силы трения и сопротивления. Любая диссипативная сила может быть представлена в виде

где v — скорость данного тела относительно другого тела (или среды), с которым оно взаимодействует; k(v) — положительный коэффициент, зависящий в общем случае от скорости v. Сила F всегда направлена противоположно вектору v.

В зависимости от выбора системы отсчета работа этой силы может быть как положительной, так и отрицательной. Однако, как мы сейчас покажем и что будет важно для дальнейшего,

суммарная работа всех внутренних диссипативных сил в системе — величина всегда отрицательная независимо от системы отсчета:

Переходя к доказательству, отметим прежде всего, что внутренние диссипативные силы в данной системе встречаются попарно, причем в каждой паре, согласно третьему закону Ньютона, они одинаковы по модулю и противоположны по направлению. Найдем элементарную работу произвольной пары диссипативных сил взаимодействия между телами 1 и 2 в системе отсчета, где скорости этих тел в данный момент равны v1 и v2:

A дис F1 v1dt F2 v2 dt.

Учтем, что F2 F1 , v1 v2 v — скорость тела 1 относительно тела 2, а также то, что F1 kv. Тогда выражение для работы преобразуется:

A дис F1 (v1 v2 )dt kvvdt kv 2 dt.

Отсюда видно, что работа произвольной пары внутренних диссипативных сил взаимодействия всегда отрицательна, а значит, и суммарная работа всех пар внутренних диссипативных сил также всегда отрицательна, причем в любой системе отсчета.

Кинетическая энергия системы

Согласно (4.28), приращение кинетической энергии каждой частицы равно работе всех сил, действующих на частицу:K i A i . Поэтому работу А, которую совершают все силы, действующие на все частицы системы, при изменении ее состояния, можно записать так: A . A i . K i . K i , или

где K — суммарная кинетическая энергия системы.

Итак, приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы:

Заметим, что кинетическая энергия системы — величина аддитивная: она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.

Уравнение (4.45) справедливо как в инерциальных, так и в неинерциальных системах отсчета. Следует только помнить, что в неинерциальных системах отсчета кроме работ сил взаимодействия необходимо учитывать и работу сил инерции.

Собственная механическая энергия системы

Только что было показано, что приращение K кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. Разделим эти силы на внешние и внутренние, а внутренние, в свою очередь, на консервативные и диссипативные. Тогда предыдущее утверждение можно записать так:

K A внеш A внутр A внеш A внутрконс A внутрдис .

Учтем, что работа внутренних консервативных сил равна,

согласно (4.33), убыли собственной потенциальной энергии сис-

темы: A внутрконс Uсоб . Тогда