Иродов И.Е. Общая физика (5 т.) / Иродов. т5 Квантовая физика Основные законы. 2014, 256с

Ангармоничность (отклонение от гармоничности), наступающая при увеличении интенсивности колебаний, приводит к тому, что с увеличением квантового числа v энергетические уровни сгущаются, и в формулу (4.23) необходимо вводить поправку на ангармоничность.

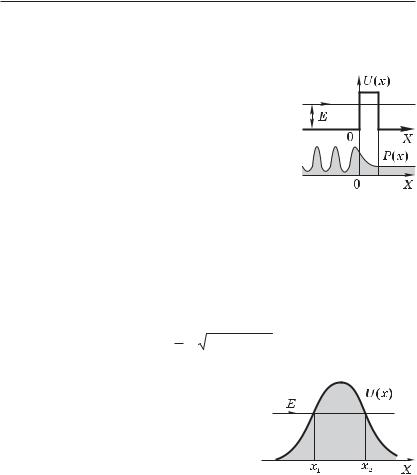
§ 4.5. Потенциальные барьеры

Сначала рассмотрим простейший случай — прямоугольный потенциальный барьер, когда потенциальная энергия U зависит только от одной координаты x, причем при x 0 претерпевает скачок (рис. 4.11). У такого барьера

Пусть слева на границу барьера налетает с

полной энергией E частица или поток час-

тиц. На языке квантовой теории это означа-

ет, что на барьер слева «падает» дебройлев-

ская волна

Рис. 4.11

Чтобы удовлетворить граничным условиям для , и ,/ x при x 0, должны существовать как прошедшая волна, так и отраженная. В этих трех волнах частота одна и та же ( E/h), поэтому в дальнейших расчетах мы можем ограничиться только координатной частью этих волн, а именно /(x).

Наша задача: сначала найти амплитуды отраженной и падающей волн, а затем — коэффициенты отражения R и пропускания D для такого барьера. Исходим из уравнения Шредингера (4.9). В нашем случае оно имеет вид

Здесь возможны два случая (см. рис. 4.11): E > U0 и E < U0.

1. В случае E > U0 общее решение уравнения (4.27) имеет вид:

Будем считать, что падающая волна характеризуется амплитудой a1, причем вещественной, а отраженная — амплитудой b1. В области x > 0 имеется только проходящая волна, поэтому b2 0. Из условия непрерывности / и /x в точке x 0 следует, что

Из совместного решения этих двух уравнений находим, что отношения амплитуд отраженной и прошедшей волн к амплитуде a1 падающей волны равны:

Для определения интересующих нас коэффициентов R и D

введем понятие плотности потока вероятности P. Скорость распространения вероятности такого потока просто совпадает с классической скоростью v частицы, и мы можем написать v p/m hk/m, поскольку согласно (3.1) p hk. Таким образом,

v T k,

и плотность потока вероятности пропорциональна величине k *:

PT k *.

Всоответствии с видом ,-функции (4.26) для падающей, отраженной и прошедшей волн мы имеем

P T k1a12 , P T k1b12 , P T k2 a22 .

Теперь можно записать выражения для коэффициентов отражения R и пропускания D:

Отсюда следует, что R + D 1, что и должно быть по определению. Кроме того, видно, что значения R и D не зависят от на-

правления движения частицы: слева направо на рис. 4.11 или наоборот.

Заметим, что в классическом случае R 0 при E > U0. 2. В случае Е < U0 формулы (4.30) остаются справедливыми.

Однако k2 будет чисто мнимым согласно (4.28). При этом выражение (4.31) для коэффициента отражения следует записать так:

Здесь числитель и знаменатель — величины комплексно-сопря- женные. Значит R 1, т. е. отражение частиц будет полным. Но /-функция при х > 0 не обращается в нуль. В самом деле, полагая k2 ik, где k 2m(U0 E)/ , получим, что /2 T e–kx и плотность вероятности местоположения частицы

Видно, что с увеличением глубины проникновения x плотность вероятности Р(х) убывает экспоненциально. Это убывание происходит тем быстрее, чем больше разность (U0 – E). Обычно глубину проникновения определяют как расстояние l, на котором Р(х) убывает в е раз. При этом в (4.33) 2kl 1 и

Можно убедиться, что для электрона при U0 – E % 10–3 эВ глубина проникновения l % 10–7 см.

Таким образом /-функция проникает в область х > 0, несмотря на то, что падающая волна отражается полностью.

В классической физике проникновение частиц под барьер запрещено, поскольку в этой области кинетическая энергия оказывается отрицательной, чего быть не может. Но мы уже знаем, что разделение полной энергии E на кинетическую и потенциальную не совместимо с соотношением неопределенностей (3.20), см. также стр. 95.

Туннельный эффект. Способность квантовых частиц в силу своих волновых свойств заходить под барьер приводит к так называемому туннельному эффекту. Он заключается в следующем. Если частица с энергией E налетает на некоторый потен-

Это приближенное равенство, оно тем точнее, чем меньше (U – E) по сравнению с Е.

физические явления; например, холодная эмиссия электронов из металлов, альфа-распад, спонтанное деление ядер и др.

Задачи

4.1.Свободное движение частицы. Найти решение временного уравнения Шредингера (4.5) для свободной частицы массы m, движущейся с импульсом p в положительном направлении оси X.

Р е ш е н и е. В этом случае потенциальную энергию частицы можно считать равной нулю U(x) 0, и уравнение (4.5) примет вид

Его решение будем искать методом разделения переменных, т. е. представим , в виде произведения двух функций, одна из которых зависит только от х, другая — только от t:

как обе части этого уравнения являются функциями независимых переменных t и х, то равенство (3) возможно лишь в том случае, если обе его части равны одной и той же константе. Из сравнения выражения (3) с уравнением Шредингера (4.9) видно, что эта константа равна E. Таким образом мы получаем два уравнения:

Их решения, как можно в этом убедиться непосредственной подстановкой, таковы:

где значения k и записаны в соответствии c постулатами корпу- скулярно-волнового дуализма.

В результате искомое решение согласно (2) будет иметь вид ,(x, t) A ei(kx – t).

Это решение будет конечным лишь при Е > 0, причем при любых значениях Е.

Именно такой вид имеет дебройлевская волна.

Плотность вероятности местоположения соответствующей частицы P(x) ,,* AA* const.

Это означает равновероятность местонахождения такой частицы во всех точках пространства (оси X). Данный вывод вполне согласуется с соотношением неопределенностей: при px 0 x , т. е. частица «размазана» равномерно по всему пространству.

4.2.Частица в прямоугольной яме с бесконечно высокими стенками.

Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками (0 < x < l). Найти вероятность местонахождения частицы в интервале (l/3, 2l/3).

Р е ш е н и е. Согласно (4.15) /-функция в основном состоянии (n 1) это / 2/l sin( x/l). Искомая вероятность

где введена новая переменная у x/l.

4.3.Найти энергию E стационарного состояния частицы массы m в одномерной прямоугольной потенциальной яме шириной l с абсо-

лютно непроницаемыми стенками, если на границе ямы (х 0) известно значение производной // x, т. е. / (0).

Р е ш е н и е. Известно, что /-функция n-го стационарного состояния определяется формулой (4.15). Взяв ее производную по х и положив затем х 0, получим:

Отсюда находим

l3 / 2

n 2 / (0).

Подставив это выражение в формулу (4.14) для энергии, имеем

El 2 [ / ( 0)]2 . 4m

4.4.Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна l и такова, что энергетические уровни расположены весьма густо. Найти плотность этих уровней dN/dE, т. е. их число на единичный интервал энергии, в зависимости от Е. Вычислить dN/dE, если

Е1,0 эВ и l 1,0 см.

4.7.Частица массы m находится в двумерной квадратной потенциальной яме с абсолютно непроницаемыми стенками. Сторона ямы равна l. Воспользовавшись результатами решения предыдущей задачи, найти значения энергии Е для первых четырех уровней.

Р е ш е н и е. В данном случае

Задача сводится к подбору таких наименьших значений n1 и n2,

Отсюда видно, что энергия Е первых четырех уровней

Е2, 5, 8 и 10 единиц 2h2/2ml2.

4.8.Воспользовавшись условием и решением задачи 4.6, найти число dN состояний частицы в интервале энергии (E, E dE), полагая, что энергетические уровни расположены весьма густо.

Ре ш е н и е. Каждому значению пары чисел n1 и n2 отвечает одно состояние частицы. Число состояний в интервале (dn1, dn2) вблизи значений n1 и n2 равно

dN dn1 dn2 .

Имея в виду уравнение k12 k22 k2, где k1 n1 /a, k2 n2 /b, отложим на осях координат величины k1 и k2. Построим затем в этом «k-пространстве» окружность радиуса k с центром в начале координат. Точки, попадающие на эту окружность, соответствуют одному и тому же значению k, а значит одной и той же энергии Е. Нaс будет интересовать только 1/4 окружности, поскольку следует рассматривать лишь положительные значения k1 и k2: отрица-

4.9.Частица массы m находится в одномерном потенциальном поле U(x) в стационарном состоянии / A exp(–7x2), где А и 7 — постоянные (7 > 0). Найти энергию Е частицы и вид функции U(x), если U(0) 0.

Р е ш е н и е. Сначала найдем вторую производную / (х) по х:

/–2A x exp(–7x2),

/–2A[exp(–7x2) x exp(–7x2)(–27x)] –2A (1 – 27x2) exp(–7x2).

Теперь подставим / и / в уравнение Шредингера:

/ 2m (E – U) / 0.

2

После сокращения на экспоненту получим:

Полагая в этом равенстве x 0 и соответственно U(0) 0, имеем