Иродов И.Е. Общая физика (5 т.) / Иродов. т5 Квантовая физика Основные законы. 2014, 256с

Исходим из уравнения Шредингера (4.9). Для одномерного случая в пределах ямы (где U 0) это уравнение упрощается:

где a и — произвольные постоянные.

Теперь самое главное: мы должны потребовать от функции /(x), чтобы она удовлетворяла естественным (стандартным) условиям. Видно, что (x) в виде (4.12) однозначна и конечна. Она должна быть еще и непрерывной, а именно, вне ямы частица быть не может, значит там /(x) 0, и для непрерывности /-функции необходимо, чтобы при x 0 и x l функция (4.12) была бы равна нулю. Из условия

/(0) a sin 0

следует, что = 0. Из условия же

/(l) a sin kl 0

в свою очередь следует, что

где n 1, 2, 3, ... (n 0 отпадает, так как при этом / 0 — частицы вообще нет).

Подставив k из (4.13) в (4.11), получим

Энергия оказалась квантованной и ее спектр — дискретный (рис. 4.1, б).

пределения /2n (x) практически «сливается» и представляется равномерным — частица начинает вести себя совсем «по-клас- сически».

Внимательный читатель по-видимому заметил, что найденные нами собственные функции (4.15) удовлетворяют не всем естественным условиям: на границах ямы /-функции не гладкие, испытывают излом. Это обстоятельство является следствием того, что на границах ямы U & , чего в реальном мире не бывает. При любом конечном разрыве потенциальной энергии /-фун- кция все равно остается гладкой (об этом подробнее ниже).

Заметим также, что в отличие от классики минимальное значение энергии Е частицы в яме согласно (4.14) не равно нулю. Это полностью согласуется с принципом неопределенности. Ведь у частицы в яме ограничена область возможных значений ее координаты, поэтому должен существовать разброс по импульсам, а значит, отлична от нуля и энергия.

Случай 2. Частица движется в одномерном потенциальном поле U(x), пока-

занном на рис. 4.3. Уже этот случай связан с достаточно громоздкими математическими преобразованиями.

Если полная энергия частицы E < U0, то говорят, что частица находится в потен-

циальной яме, или в связанном состоянии. Будь частица классической, она не смогла бы при этом условии выйти за пределы ямы, поскольку там ее кинетическая энер-

гия была бы отрицательной, что невозможно. Отражаясь от стенок ямы, частица двигалась бы только в ее пределах и могла быть с равной вероятностью обнаружена в любом месте ямы.

Существенно иначе ведут себя частицы, подчиняющиеся квантовым законам. Чтобы выяснить, как именно, воспользуемся уравнением Шредингера (4.9) в одномерном виде. Поскольку функция U(x), как видно из рис. 4.3, является ступенчатой, то удобно разбить область изменения x на два участка, (1) и (2), с постоянными значениями U, получить решения для каждого участка, а затем «сшить» эти решения так, чтобы /-функция была непрерывной и гладкой.

94 Глава 4

Снабдим решения на участке 1 индексом 1, а на участке 2 — индексом 2. Теперь запишем уравнение Шредингера для этих

Общие решения этих уравнений имеют вид

/1(x) a sin(kx ), /2(x) be–kx cekx.

Они должны удовлетворять естественным условиям. Из условия непрерывности /-функции, учитывая, что при x i 0 /1 2 0, имеем /1(0) 0, откуда 0. Из требования конечности /-функ- ции следует, что коэффициент c 0, поскольку экспонента с положительным показателем соответствует непрерывному росту вероятности обнаружения частицы в области 2 с увеличением глубины проникновения х. И наконец, требование непрерывности и гладкости /-функции в точке x l означает, что

где C h/2ml2U0 .

Изобразив графики левой и правой частей этого уравнения (рис. 4.4), найдем точки пересечения прямой с синусоидой. При этом корни данного уравнения, отвечающие собственным значениям Е, будут соответствовать тем точкам пересечения, для которых tgkl < 0 согласно (4.18). Это значит, что корни уравнения (4.19) должны находиться в четных четвертях окруж-

Например, первый уровень, как следует из этого рисунка, появляется при условии kl /2, когда Ckl 1, откуда E U0. Второй уровень — при kl (3/2) и т. д.

Таким образом, в данной яме при E < U0 спектр собственных значений энергии E оказыва-

ется дискретным. Этим значениям соответствуют связанные состояния частицы и характеризующие эти состояния /-функции, одна из которых показана на рис. 4.5.

Следует еще раз отметить, что такая потенциальная яма, как показывает расчет и график на рис. 4.4, может не содержать и ни одного уровня (это будет при условии l2U0 < 2 h2/8m). В этом случае движение частицы не локализовано в конечной области,

еедвижение, как говорят, инфинитно.

Нельзя не обратить внимания на тот удивительный (с точки

зрения классики) факт, что частица, будучи в связанном состоянии, может оказаться и в области 2 (см. рис. 4.3), где ее полная энергия E < U0. Объясняется это тем, что равенство E K U в квантовой теории теряет смысл: кинетическая K и потенциальная U энергии в силу принципа неопределенности не могут одновременно принимать точные значения. В самом деле, U зависит от координат, а K — от импульса частицы. Поэтому не следует удивляться тому, что в некоторых местах полная энергия Е < U.

Отметим также, что с ростом, например, глубины ямы, т. е. U0, число уровней энергии E и связанных состояний будет увеличиваться, а вероятность обнаружения частицы в области 2

96 Глава 4

будет становиться все меньше, и при U0 & она обратится в нуль, /-функция в точке x l приобретает излом (теряет гладкость), с чем мы и столкнулись в случае 1 и наблюдаем в данной яме в точке x 0.

Уместно здесь коснуться вопроса о гладкости /-функции в месте конечного разрыва* функции U(x). Проинтегрируем уравнение Шредингера по малому интервалу координаты х, внутри которого имеется скачок U(x), например, в точке х 0. В результате получим

где координату х берем в малом интервале (–3, 3). Ввиду конечности скачка U(0) интервал при 3 & 0 тоже стремится к нулю. Отсюда и следует, что слева и справа от точки x 0 производные // x будут одинаковы, значит /-функция оказывается гладкой.

§ 4.4. Квантовый гармонический осциллятор

Задача об уровнях энергии одномерного гармонического осциллятора является одной из наиболее важных задач о собственных значениях.

В квантовой теории понятие силы теряет смысл (см. сноску на стр. 85), поэтому квантовый гармонический осциллятор следует определить как поведение частицы массы m с потенциальной энергией U(x) такой же, как у классического осциллятора, а именно

где k — постоянная. Графиком функции (4.20) является парабола (рис. 4.6). Согласно классической механике осциллятор совершает гармонические колебания с циклической частотой

*Говоря о «разрыве», мы должны понимать этот термин не в математическом, а в физическом смысле: функция U(x) меняется от одного значения до другого в очень малой области пространства, испытывая по существу скачок. Именно поэтому в таком месте график U(x) изображают практически вертикальным отрезком.

k/m. В квантовой теории это равенство следует рассматривать просто как введение некоторой новой постоянной (и не более), однако, как будет видно в дальнейшем, это делается неспроста. Сейчас же, выразив в формуле (4.20) k через и m, получим

Теперь обратимся к уравнению Шредингера (4.9), которое в нашем одномерном случае будет иметь вид

Нахождение решения этого уравнения, т. е. /-функции, является громоздкой математической задачей. Для нас главное не в этом. Оказывается, уравнение (4.22) имеет конечные, однозначные, непрерывные и гладкие решения (собственные функции) при собственных значениях Е, равных

ских уровней (4.23) дана на рис. 4.7. Видно, что эти уровни — эквидистантны, т. е.

отстоят друг от друга на одинаковую величину. Минимальная энергия E0 h /2, ее называют нулевой энергией. То, что минимальная энергия квантово-

го осциллятора не равна нулю (частица не может «лежать» в нижней точке параболической потенциальной ямы), связано с принципом неопределенности, как и в случае прямоугольной ямы. Если бы энергия

частицы была равна нулю, то частица покоилась бы, и ее импульс и координаты имели бы одновременно определенные значения, что противоречит принципу неопределенности.

Колебания молекул. В атомной физике к осциллятору сводится задача о колебаниях молекул и многие другие важные задачи. Применим полученные выводы к колебаниям, например, двухатомных молекул.

На рис. 4.9 изображена потенциальная энергия U взаимодействия

атомов в двухатомной молекуле (типа NaCl) в зависимости от расстояния r между ядрами атомов. Из

вида кривой U(r) следует, что атомы в молекуле могут совершать колебания относительно равновесного расстояния r0 между ядрами, и у моле-

кулы, следовательно, должны существовать дискретные колебательные уровни энергии. Они описываются той теперь под надо понимать 0 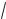k/ молекулы, m1m2/(m1 m2).

Приведем в качестве примера циклические частоты некоторых двухатомных молекул:

Нижняя часть потенциальной кривой на рис.

4.9 совпадает с параболой (она изображена пунктиром), поэтому при малых колебаниях молекулы ведут себя как идеальные, гармонические

осцилляторы, и их нижние колебательные уровни должны быть эквидистантны, как показано на рис. 4.10.

Наличие дискретных колебательных уровней

Рис. 4.10

приводит к появлению в молекулярных спектрах линий, связанных с переходами между этими уровнями в

соответствии с правилом отбора (4.24), и поэтому весь колебательный спектр должен состоять из одной линии (см. pис. 4.10). Впрочем при этом наблюдается не чисто колебательный, а так называемый колебательно-вращательный спектр (см. § 5.3).