24.Аналітична функція. Диференціал.

Означення. Однозн. Функція називається аналітичною в т. z, якщо вона дифер.(викон умови Коші-Тім) в т. z і в деякому її околі. Функція 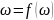називається аналіт. В області D (однозв’язн. відкр.) , якщо вона дифер в кошн. т-ці цієї області. Тільки якщо ф-ція є аналітичною наз. Поавильними , а тільки, в яких умова аналітичності поруш, називається особливими.

Нехай функція 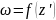- аналіт. В т. z , тоді 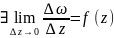, отсюда 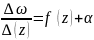, де 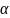-нехай мала величина вищого порядку малості ніж

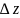
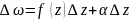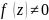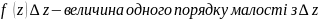, якщо , то , а 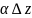– нескінченно мала величина вищого порядку малості ніж

Означення. Дифер аналіт функції наз гол ч-на приросту функції 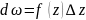або 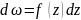оскільки при

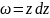
25.Гармонічні функції.

Нехай задана аналітична функція 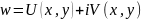; w-дифер. U(x,y),V(x,y) – мають част похибки.

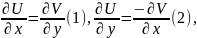візьмемо в (1) похідну по х, і в (2) по y. 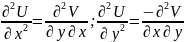Додамо ці рівняння 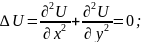Означення: Рявняння 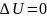назив рівнянням Лапласа, а 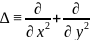- оператор Лапласа. Означення: Функція U(x,y) , що має неп пох до 2-го пор включно, і задов. р-тю Лапласа назив гармонічною. Ми довели, що для аналіт ф-ції w=U(x,y)+iV(x,y) також гарм.

26.Інтегрування функцій комплексної змінної. Основні властивості інтегралів від функцій комплексної змінної.

Нехай на гладк кривій L від точки z0 до точки z задана непер функція f(z). Розіб’ємо L на n част від точки z0 до z точками. візьмемо довільну т-ку Ск і складемо інтегр суму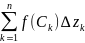 Границя інтегр сум прямує до нуля, довжину найбільшої з дуг 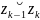(якщо вона існує назив інтегралом від ф-ції f(z) по кривій L і познач 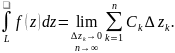Покажемо, що якщо L гладка крива, а f(z) непер і однозначна на L, то інтегр в існує. Нехай 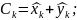f=U(x,y)+iV(x,y);

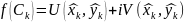
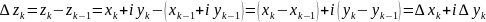
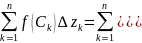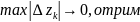
Припущ стосовно L і f(z) в правій част інтегр суми відпов ф-ції і границі цих сум існують. Отже, перейшовши до границь при 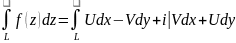; 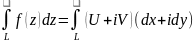Якщо L задана x=x(t),y=y(t), 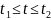, то z=z(t)=x(t)+iy(t), тоді 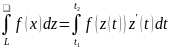Дійсно:

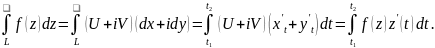
Властивості:

1)

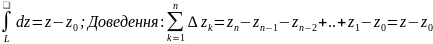
2)

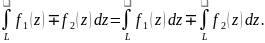
3)

4)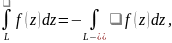 тобто якщо змін напрям інтегрування, то інтеграл змінює свій знак на протилежний.

5)

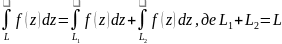
6)(оцінка модуля інтегрування) Якщо 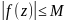для всіх точок 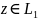, то

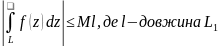
27.Основна теорема Коші і наслідки з неї.

Теорема Коші

Нехай функція f(z) –аналіт в однозв’язн області D. Тоді для довільної замкненої кривої L, що цілком лежить в D , викон

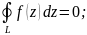
Доказ. Припустимо, що f(z) має неперервні похідні в області D

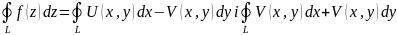
f(z) – анал. Отже викон умова Коші – Рімора

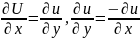
Тоді за формулою Гріна інтеграли в правій наст. Дор. 0 , отже

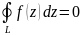
Доказано.

Наслідок 1 : якщо область D обмежена складним додатньо орієнтованим контуром

L=L₀+L₁…+L_n, т.б при обході по контуру точки області D лежать зліва , то при умові аналітичності функції f(z).

Наслідок 2 : Якщо обл. D обмежена зовнішнім контуром L а всередині контуром L_1..Ln, що орієнтована протягом годинникової стрілки, і f(z)-анал., то ;

Наслідок 3: якщо f(z) аналіт в однорідній області D, то інтеграл по кривій АВ не задежить від контуру інтегрування , а залежить лише від початка і кінця т-к інтегрування

Доказ: З’єднаємо точки А і В 2-ма довільними кривими отримаємо

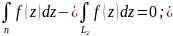
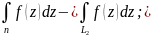доказ закінченно

Має сенс запис 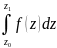; якщо -зафікс, то (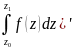 =F(z)

Можна довести, що якщо f(z)- аналітична, то F(z) – також аналітична

Функція F(z) називається первісною для f(z)

Множина всіх первісних F(z)+C називається невизначеним інтегралом функції

Нех. F(z)-первісна = F(z)+C.

Підставимо замість z точку z₀ отримаємо F(z₀)+C=0 випливає F(z₀)=C. Отже

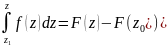– формула Ньютона – Лейбніца