Лекція 11 Ряд Лорана

z z0

f z an

n

(5.1)

Розглянемо більш загальні ряди по додатних і від’ємних степенях

z z0 ,

тобто ряди вигляду:

z z0

S z an

n ;

(5.2)

n

які можна розуміти як суму двох рядів,

z z0 n

an z z0 n ,

a n

(5.3)

n 0

n 1

і які збігається в області, де збігаються

обидва ряди (5.3).

Припустимо, що ряд

an z z0

n

збігається

в крузі

z z0

R,

а ряд

n 0

a n z z0 n

збігається

в області

z z0

r. Якщо

r R, то

в

області

n 1

K z

r

z z0

R збігатиметься ряд (5.2). Це кільце може виродитися в круг

z z0

R з “виколотою” точкою z z0

(при r 0,

R ),

в усю комплексну

площину з “виколотою” точкою z z0

(при r 0, R ), у зовнішню частину

круга

z z0

r

(при r 0,

R ).

Доведемо, що сума ряду (5.2) є аналітичною функцією в області K.

Для цього, очевидно, нам досить довести, що сума ряду

z0 n

z a n z

(5.4)

n 1

буде аналітичною функцією в області K (сума другого ряду,

як показано вище,

– аналітична функція).

1

Зробимо заміну

, тоді ряд (5.4) запишеться у вигляді степеневого

z z0

76

a n n .

n 1

тоді сума є ана-

Нехай його радіус збіжності дорівнює :

0 ,

1

літичною функцією в крузі

, а

, якщо її розглядати як функцію

z z

0

від z, є аналітичною всюди, крім точки z z0 .

Тоді за властивістю 20 функція z буде аналітичною функцією в області

збіжності ряду (5.4), тобто поза кругом

z z

0

1

r.

ласти в ряд вигляду (5.2) ? Позитивну відповідь дає

Теорема (Лорана). Кожну функцію

f z , однозначну і аналітичну в кру-

говому кільці r

z z0

R, можна розкласти в цьому кільці в ряд

f z an z z0 n ,

f z

n

де an

1

dz, n 0, 1, 2,..., L

– довільне коло з центром в точці z0 ,

n 1

2 i

L

z z

0

яка лежить всередині кільця.

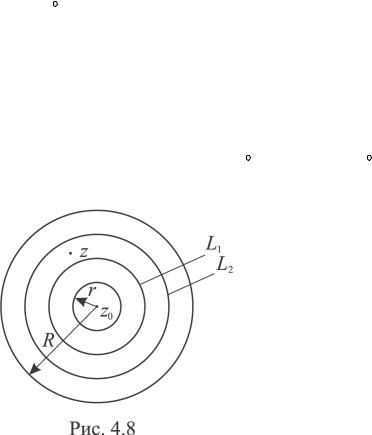
Візьмемо довільну точку z

кільця

r

z z0

R і проведемо всередині

два кола L1

і L2 із спільним центром у точці z0 і так, щоб точка z лежала все-

редині L2 і зовні L1 (рис.4.8). За формулою (4.5) маємо

1

f

1

f

f z

L

d

L

d .

2 i

z

2 i

z

2

1

Ряд

an z z0 n називається правильною частиною ряду Лорана, а ряд

a n

n 0

– головною частиною цього ряду.

z z 0

n

n 1

f z у крузі

Раніше було доведено, що коли функцію

z z0

R можна ро-

зкласти в степеневий ряд по степенях z z0 ,

то цей ряд єдиний і є рядом Тей-

лора даної функції.

5.2. Нулі функції

Нехай функція

f z

– аналітична в області D і

z0 D. Точка z0

назива-

ється нулем функції

f z порядку m, якщо виконуються умови

f z0 f z0 ... f m 1 z0 0,

f m z0 0,

(5.9)

тобто розклад функції в ряд Тейлора в околі точки z0 має вигляд

f z am z z0 m am 1 z z0 m 1 ..., am 0.

(5.10)

Зокрема, якщо m 1,

то точка z0 називається простим нулем.

Теорема. Для того щоб точка z0

була нулем m -го порядку функції f z ,

аналітичної в точці

z0 необхідно і достатньо, щоб в деякому околі цієї точки

виконувалась рівність

f z z z0 m z ,

(5.11)

де функція z аналітична в точці z0 і z0 0.

Достатність.

Нехай в деякому околі точки

z0 виконується

рівність

(5.11), тоді функцію z в цьому околі можна розкласти в степеневий ряд

z b0 b1 z z0 b2 z z0 2 ...,

де b0

z0 0. Тому

f z z z0 m b0

b1 z z0 b2 z z0 2 ...

b z z

0

m b

z z

0

m 1

b

z z

0

m 2 ...

0

1

2

b0 0, тобто z0 є нулем порядку m функції

f z

.

79

5.3. Ізольовані особливі точки і їх класифікація

Точки, в яких порушується аналітичність функції, називаються особливи-

ми. Особлива точка

z z0 функції f

z

називається ізольованою, якщо в де-

якому її околі функція

f z

на має других особливих точок.

f z

Ізольовану особливу

точку z z0

однозначної

аналітичної функції

називатимемо:

f z в точці z z0 ;

а) усувною, якщо існує скінченна границя функції

б) полюсом, якщо lim

f z ;

z z0

f z

в) істотно особливою точкою, якщо в точці z z0

функція

не має

границі ні скінченної, ні нескінченної.

f z

Теорема 1. Для того,

щоб точка z z0 була полюсом функції

необхі-

дно і достатньо, щоб вона була нулем для функції z

1

.

f z

Достатність.

Нехай точка z z0

є нулем функції z

1

,

тобто

f z

z0 0. Тоді lim

1

lim z 0,

звідки lim f z .

f

z

z z0

z z0

z z0

Необхідність.

Нехай

lim f z .

Тоді функція

z

1

має в точці

f z

z z0

z z0 границю, що дорівнює 0, тобто

z

0

– усувна особлива точка функції z .

Якщо покласти z0 0,

то функція z

буде аналітичною в околі точки z0 , а

точка z0 буде її нулем.

Ця теорема дає можливість дати таке означення:

f z , якщо вона

Точка z z0 називається полюсом порядку m для функції

є нулем порядку m для функції z

1

.

f z

Використовуючи теорему п. 5.2. неважко довести таку теорему

Теорема 2. Для того, щоб точка

z z0 була полюсом порядку m функції

f z

z

,

z z0 m

де z – аналітична в точці z0

і z0 0,

або, щоб існувала не рівна нулю скі-

нченна границя

lim z z0 m f z C .

z z0

З’ясуємо, як зв’язана поведінка функції f z

в околі ізольованої особливої

стив головної частини,

тобто, щоб коефіцієнти an

0 для

n 1, 2,....

2. Для того, щоб точка z0 була полюсом порядку m функції

f z необхід-

но і достатньо, щоб головна частина ряду Лорана для

f z в околі точки

z0 містила лише скінченне число членів і коефіцієнт

a m 0, а

an 0

для n m 1 , m 2 ,... .

f z ,

3. Для того, щоб точка z0

була істотно особливою точкою функції

необхідно і достатньо, щоб головна частина ряду Лорана для

f z в

околі точки z0 містила нескінченну кількість членів.

Доведемо, наприклад, перше твердження

Достатність. Нехай в околі 0

z z0

R ряд Лорана має вигляд