Лекція 9 Функ. компл. змінної

Лекція 9. Функції комплексної змінної.

Означення функції комплексної змінної Криві і області в комплексній площині Границя функції комплексної змінної Неперервні функції Функціональні ряди Степеневі ряди

Елементарні функції комплексної змінної

2.І. Означення функції комплексної змінної

Кажуть, що на множині D C визначена функція w f z , якщо кожно-

му комплексному значенню z D ставиться у відповідність одне (однозначна функція) або декілька (многозначна функція) значень w які належать деякій множині E C.

Множина D називається областю визначення, а множина Е – множиною значень функції f z .

Якщо z x iy, а w u iv, то функцію w f z можна задати з допомо-

гою двох дійсних функцій

u u x, y , v v x, y : w f z u x, y iv x, y .

Таким чином функція w f z здійснює відображення точок z – площини на відповідні точки w-площини.

Розглянемо наприклад функцію w z 2 iz. Тоді

w u iv x iy 2 i x iy x 2 2xyi y 2 xi y x 2 y 2 y i 2xy x .

Тому рівність w z 2 iz рівносильна двом рівностям u x2 y2 y,

v 2xy x.

16

де x t , y t неперервні функції дійсної змінної t. Рівняння (2.1) це пара-

метричні рівняння кривої , а (2.2) – комплексне параметричне рівняння кривої

.

одночасно не дорівнюють нулю.

Гладка крива у кожній своїй точці має дотичну, причому нахил дотичної змінюється неперервно, коли точка дотику переміщується по кривій.

Якщо крива складається із скінченого числа гладких кривих, то вона на-

зивається кусково-гладкою.

Множина комплексних чисел D називається областю, якщо D, як множи-

на точок площини, відкрита і зв’язна.

Нагадаємо, що множина називається зв’язною, якщо довільні дві її точки можна з’єднати неперервною кривою, яка повністю лежить в цій множині;

множина називається відкритою, якщо разом з кожною своєю точкою вона міс-

тить деякий окіл цієї точки.

Область D називається однозв’язною, якщо довільна неперервна замкнута самонеперетинаюча крива, проведена в D, обмежує деяку область G, яка цілком належить D.

У противному разі область D називається многозв’язною. Вся комплексна площина є однозв’язна область. Однозв’язні області є також круг z z0 R і

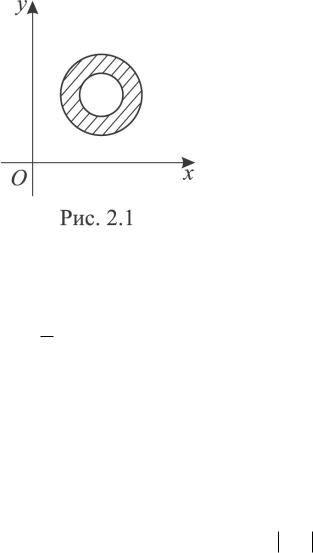
півплощина Re z 0. Кільце (рис.2.1) многозв’язна область (двохзв’язна).

17

Крива, що обмежує область D називається межею області D.

Область D разом із своєю межею називається замкненою областю і поз-

начається D.

Область D називається обмеженою, якщо можна вказати круг певного радіуса, який цілком містить в собі D. В противному разі область D називається

необмеженою.

Розглянемо, наприклад, множину точок z, які задовольняють нерівності

2 z i 3.

Це множина точок, які містяться між двома колами радіусів 2 і 3 і з спі-

льним центром у точці z i, т.т. це кільце і є обмеженою многозв’язною

(двозв’язною) областю.

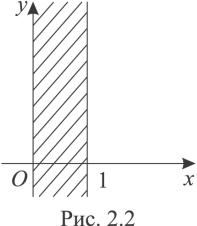
Множина точок, які задовольняють нерівність

0 Re z 1

є замкненою необмеженою областю. Прямі Re z 0 і Re z 1 утворюють межу цієї області (рис.2.2).

18

Це означення коротко можна записати так:

Означення границі функції комплексної змінної f z аналогічне з озна-

ченням границі дійсної функції дійсної змінної, лише замість абсолютної вели-

чини використовується модуль комплексного числа. Тому багато властивостей границь дійсних функцій дійсної змінної переноситься на границі функцій ком-

плексної змінної. Зокрема,

Доведення цих властивостей можна звести до відповідних властивостей границь дійсних функцій двох змінних, оскільки вірна.

Аналогічно дається означення границі в нескінченно віддаленій точці:

Легко переконатись у справедливості таких тверджень:

2.5. Функціональні ряди

Функціональним рядом називається вираз

n 1

збіжний, множина всіх точок z, в яких ряд (2.3) збіжний називається областю його збіжності.

Якщо ряд (2.3) збіжний на множині D, то його сума буде деякою функці-

єю від z, визначеною на D. Позначимо її через

n

rn z S z Sn z S z fk z – п-й залишок ряду.

k 1

22

Для дослідження ряду на рівномірну збіжність користуються такою дос-

татньою умовою рівномірної збіжності.

Теорема. (Ознака Вейєрштрасса). Ряд (2.3) збіжний на множині D абсо-

лютно і рівномірно, якщо існує знакододатній збіжний числовий ряд an , та-

n 1

кий, що fn z an , z D.

Відмітимо одну з властивостей рівномірно збіжних рядів: сума членів рів-

номірно збіжного на деякій множині ряду неперервних функцій є функція, непе-

рервна на цій множині.

2.6. Степеневі ряди

Степеневим рядом в комплексній області називається функціональний

ряд вигляду:

Для дослідження цих рядів на збіжність в інших точках комплексної площини користуються теоремою Абеля. Сформулюємо її для ряду (2.5).

Теорема. Якщо ряд (2.5) збіжний в точці z z0 0, то він абсолютно збі-

жний і при всіх значеннях z, для яких z z0 . Якщо ряд (2.5) розбіжний в точці z z1, то він розбіжний і при всіх значеннях z, для яких z z1 .

Доведення цієї теореми таке саме, як і для степеневих рядів в дійсній об-

ласті. З неї випливає існування такого числа R 0, що для всіх z R степене-

вий ряд (2.5) збіжний, а при z R розбіжний.

Круг радіуса R, де 0 R , з центром у початку координат, всередині якого степеневий ряд (2.5) абсолютно збіжний, а зовні якого розбіжний, нази-

вають кругом збіжності цього ряду, а число R – радіусом збіжності. Якщо ряд

(2.5) збіжний тільки в точці z 0, то вважають R 0, а якщо він збіжний в усій площині, то R .

Круг збіжності ряду (2.4) матиме центр в точці z z0 .

На межі круга збіжності, тобто, в точках z, де z R , ряд може бути як

збіжним так і розбіжним, але якщо в деякій точці на колі ряд абсолютно збіж-

ний, то він збіжний абсолютно у всіх точках кола.

Радіус збіжності рядів (2.4) і (2.5) можна знаходити так само, як і для ря-

дів з дійсними членами, тобто за формулами

якщо відповідні границі існують.

Слід відмітити, що степеневий ряд збіжний рівномірно в кожному за-

мкненому крузі, який цілком міститься в середині круга збіжності цього ряду, а

24

тому його сума неперервна в середині круга збіжності цього ряду.

Розглянемо тепер ряд

початку координат.

Розглянемо ряд, який складається з рядів виду (2.4) і (2.8):

Область збіжності ряду (2.11) це круг деякого радіусу R з центром в поча-

тку координат О, а область збіжності ряду (2.12) це зовнішність деякого круга радіуса r з центром О. Якщо r R, то спільна частина цих областей збіжності це кільце з центром О. (рис.2.3), яке є областю абсолютної збіжності ряду

(2.10). Воно називається кільцем збіжності ряду (2.10). Якщо r R, то ряд

(2.10) розбіжний, якщо r R, то він може збігатись тільки на колі радіуса r R.

25