14.Тригонометричний ряд Фур’є.

О: Тригонометричним рядом називається функціональний ряд вигляду:

Де 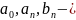дійні числа (коефіцієнти ряду)

1.1 зокрема записується так:

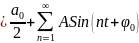
15.Теорема Діріхлє про розклад в ряд Фур’є 2π-періодичних функцій. Розклад в ряд Фур’є парних і непарних функцій.

Нехай функція f(x) - 2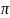 періодична і інтегрована на і має місце розклад в ряд Фур’є.

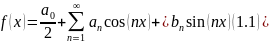
Проінтегруємо 1.1 і межах

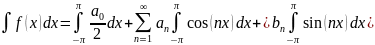
Поможемо 1.1 на cosmx і проінтегруємо на

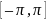
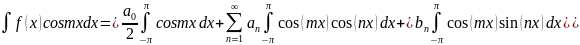
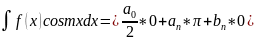
Також помножимо 1.1 на sinmx і проінтегруємо на

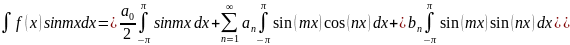
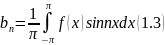
Для інтеграла 2 періодичної функції f(x) можна записати:

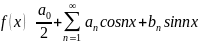
Де знаходимо з формул вище.

Теорема Діріхле: нехай 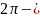періодична функція f(x) на задовільняє умови:

1.) f(x) – кусково періодична на

2.) f(x) – кусково монотонна

Тоді ряд Фур’є зводиться до функції f(x) в точках де функція неперервна.

В точках розриву (x₀).

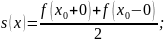
На границі відрізку

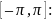
16. Розклад в ряд Фур’є функцій довільного періоду. Представлення неперіодичної функції рядом Фур’є.

Нехай функція 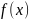має період

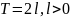
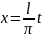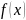Зробимо заміну . Тоді функція буде дорівнювати функції .

визначена на

При

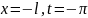
При

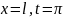
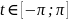
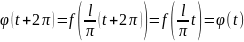
Тому для 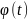має місце розклад в ряд Фур’є.

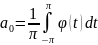
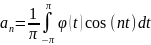
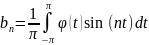
Повернемось до змінної 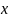, при цьому: ,

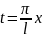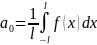
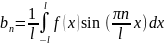
І ряд Фур’є буде мати вигляд

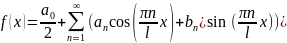
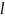Зауваження. Всі викладки для -періодичної функцію мають місце і для 2 -періодичних функцій.

Якщо -неперіодична, то представити її у виді ряду Фур’є – неможливо.

Якщо ж потрібно представити у вигляді ряду Фур’є на 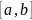, на якому вона задовольняє умови теореми Діріхлє, то переносимо початок координат всередину і записуємо функцію 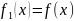при

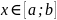
Робимо функцію 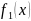- 2 -періодичною, де 2 =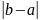 . розкладаємо в ряд Фур’є. Ряд Фур’є буде збігатися до тільки на цьому проміжку, а далі – це зовсім інші функції.

Якщо потрібно розкласти в ряд Фур’є функцію, задану на , то:

1. За 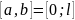і за поперечний виклад будуємо

2. Можна продовжити функцію на 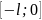довільним чином, а потім розкладемо в ряд Фур’є як 2 -періодична.

Зокрема можна продовжити на парним, або непарним чином.

17.Комплексні числі і дії над ними.

z=x+iy – алгебраїчна форма комлексного числа y

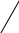
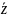=x-iy – спряжене комплексне число r

i²=-1, i=

y=Rez – дійсна частина x

y=Imz – уявна частина

|z|=r – модуль комплексного числа,

аrgz – головне значення аргумента

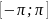
Argz=argz+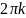

argz=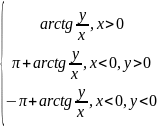

x=rcos

y=rsin

z=r(cos +isin ) – тригонометрична функція комплексного числа

z=r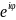 – показникова функція комплексного числа

; ;

; ;

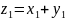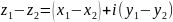
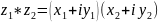
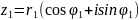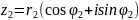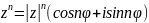– формула Муавра

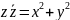– дійсне число

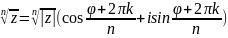
Де k=0, 1, 2, …, n-1

18.Функції комплексної змінної. Основні поняття.

Нехай в комплексній площині маємо дві множини D i E. На множині D будемо зображувати комплексні числа z=x+iy, а на множині E – комплексні числа .

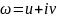Якщо кожному числу zєD ставиться у відповідність єдине число 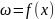, то кажуть, що задана однозначна функція

Якщо при якомусь z=D значень більше одного, то функція – багатозначна.

Приклад:

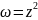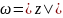1. , - однозначна

2. – багатозначна

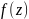Область D називається областю визначення функції , а область E₁єE називають областю визначення функції

;

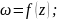
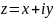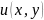– дійсна частина

– уявна частина

Таким чином функція комплексної змінної може задаватись двома функціями від двох змінних