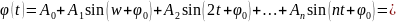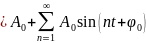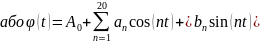- •1.Числові ряди. Основні властивості та дослідження ряду геометричної прогресії.
- •2.Основні властивості числових рядів.
- •3.Ознака порівняння та гранична ознака порівняння для знакододатних рядів.
- •4.Ознака д’Аламбера, радикальна ознака Коші.
- •5.Інтегральна ознака коші.
- •6.Ряди, в яких знаки членів строго чергуються. Ознака Лейбніца.
- •7.Знакозмінні ряди. Абсолютна і умовна збіжність.
- •Доказано.
- •8.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейерштрасса.
- •9.Степеневі ряди. Теорема Абеля. Інтервал та радіус збіжності степеневого ряду.
- •10.Властивості степеневих рядів.
- •11.Ряди Тейлора і Маклорена.
- •12.Наближені обчислення за допомогою степеневих рядів.
- •13.Ряди Фур’є. Гармонічні коливання.
- •Доказано.
- •Доказано.
- •14.Тригонометричний ряд Фур’є.
- •15.Теорема Діріхлє про розклад в ряд Фур’є 2π-періодичних функцій. Розклад в ряд Фур’є парних і непарних функцій.
- •16. Розклад в ряд Фур’є функцій довільного періоду. Представлення неперіодичної функції рядом Фур’є.
- •17.Комплексні числі і дії над ними.
- •18.Функції комплексної змінної. Основні поняття.
- •19.Границя і неперервність функції комплексної змінної.
- •20.Елементи функції комплексної змінної
- •22.Елементи функції комплексної змінної , і зв’язок між ними.
- •23. Диференціювання функцій комплексної змінної. Умови Коші-Рімана.
- •24.Аналітична функція. Диференціал.
- •25.Гармонічні функції.
- •26.Інтегрування функцій комплексної змінної. Основні властивості інтегралів від функцій комплексної змінної.
- •27.Основна теорема Коші і наслідки з неї.
- •28.Первісна і невизначений інтеграл від функції комплексної змінної. Формула Ньютона-Лейбніца.
- •29.Інтегральна формула Коші і наслідки з неї.
- •30.Числові ряди в комплексній площині. Необхідна умова збіжності та теорема про абсолютну збіжність таких рядів.
- •31.Степеневі ряди в комплексній площині. Теорема Абеля. Властивості степеневих рядів.
- •32.Ряд Тейлора для функції комплексної змінної.
- •33.Ряд Лорана.
- •34.Нулі аналітичної функції.
- •35.Ізольовані особливі точки і їх класифікація.
- •36.Нескінченно віддалена особлива точка.
- •37.Означення лишку. Теорема Коші про лишки.
- •38.Обчислення лишків.
- •39.Застосування лишків до обчислення дійсних визначених інтегралів.
- •40.Оригінали і їх зображення. Теореми про існування зображення та єдність оригіналу.
- •41.Властивості перетворення Лапласа: лінійність, подібність, зміщення.
- •Доказано.
- •46.Обернене перетворення Лапласа. Теореми розкладу.
- •47.Випадкові події. Класичне означення ймовірності. Властивості ймовірності.
- •48.Відносна частота. Означення статичної і геометричної ймовірностей.
- •49.Теорема додавання ймовірностей несумісних подій. Повна група подій. Протилежні події.
- •50.Умовна ймовірність. Теорема множення ймовірностей. Незалежність подій.
- •51.Теорема про ймовірність суми сумісних подій.
- •52.Формула повної ймовірності.
- •Доказано.
- •53.Формула Байеса (теорема гіпотез).
- •Доказано.
- •54.Незалежні випробування. Формула Бернулі.
- •Доказано.
- •55.Оцінка найбільш ймовірного числа появи дискретної випадкової величини.
- •56.Теорема Пуассона.
- •57.Локальна та інтегрально теореми Муавра-Лапласса.
- •58.Математичне сподівання дискретної та неперервної випадкових величин та його властивості.
- •Доказано.
- •Доказано.
- •Доказано.
- •59.Дисперсія і середнє квадратичне відхилення.
- •60.Неперервні випадкові величини та функція ймовірності розподілу.
10.Властивості степеневих рядів.
1)Cтепеневий
ряд є абсолютно і рівномірно збіж. на
довільному відрізку
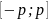 ,
що цілком лежить в інтервалі збіжності
(-R;R)
,
що цілком лежить в інтервалі збіжності
(-R;R)
Доведення:
За
умовою
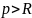 Візьмемо
Візьмемо
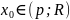 За
теоремою Абеля
За
теоремою Абеля
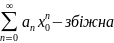 .
Візьмемо
.
Візьмемо
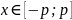
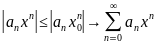 – абс.
І рівном. Збіж.
– абс.
І рівном. Збіж.
2) Сума степеневого ряду неперерв. Ф-ією на інтервалі його збіжності.
3)
Якщо
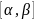 міститься в інтервалі збіжності
степеневого ряду, то можна інтегрувати
почленно ряд. Зокрема, якщо взяти відрізок
міститься в інтервалі збіжності
степеневого ряду, то можна інтегрувати
почленно ряд. Зокрема, якщо взяти відрізок
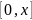 ,
,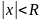 ,
то
отримаємо ряд інтервал збіжності якого
збіг. З інтервалом збіжності нашого
ряду.
,
то
отримаємо ряд інтервал збіжності якого
збіг. З інтервалом збіжності нашого
ряду.
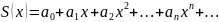
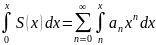
4)
Якщо
степеневий ряд має інт. Зб. (-R;R)
то
ряд, утвор диференціюванням цього ряду
має той самий інтеграл збіжності, тобто
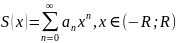 ,
,
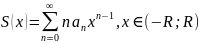
11.Ряди Тейлора і Маклорена.
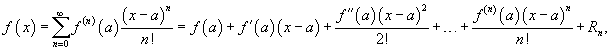
Там де а – треба х0
Де
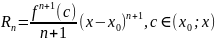 – залишковий член у форм Лагранжа
– залишковий член у форм Лагранжа
Многочлен Тейлора:
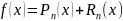
Якщо функція f(x) нескінченно разів диферент в околі точки, то для неї має місце ряд Тейлора.
Ряд Мааклорена утв з ряду тейлора при х0=0
![]()
Теорема1:
Для того, щоб ряд Тейлора збігався до
функції f(x)
необхідно
і достатньо, щоб
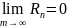
Теорема2:
Якщо всі похідні функції f(x)
в
околі т. х0 обмежені деяким числом М
 то
ряд Тейлора збігається до f(x)
то
ряд Тейлора збігається до f(x)
12.Наближені обчислення за допомогою степеневих рядів.
Нехай
потрібно обчислити значення функції
f(x)
при
x
= x0,
функція
f(x)
розкладується
в ряд Тейлора в околі точки x0.
f(x0)
– це
сума ряду S(x0).
Наближене
значення f(x0)
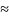 S(x0),
при
цьому похибка |r0(x0)|
= |Un+1(x0)
+
Un+2(x0)
+ +
… |. Причому,
якщо ряд для f(x),
такий, що знаки
якого строго чергуються то похибка
S(x0),
при
цьому похибка |r0(x0)|
= |Un+1(x0)
+
Un+2(x0)
+ +
… |. Причому,
якщо ряд для f(x),
такий, що знаки
якого строго чергуються то похибка
|r0(x0)| < |Un+1(x0)|
Якщо ряд, знакододатній або закозмінний, то похибку оцінюють так:
|rn(x0)| = |Un+1(x0) + Un+2(x0) + … | |Un+1(x0)| + |Un+2(x0)| + … < a1 + a2 + …
Де - числовий ряд, сума якого можна знайти.
Наближене обчислення визначеного інтеграла.
Нехай
потрібно обчислити f(x)
=
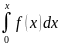 ,
який або не виражений в елементарних
функціях, або важко обчислюється. Якщо
фукція f(x)
розкладається в степеневий ряд, а
проміжок інтегрування [0,x]
належить області збіжності цього ряду,
то отримаємо функцію F(x).
,
який або не виражений в елементарних
функціях, або важко обчислюється. Якщо
фукція f(x)
розкладається в степеневий ряд, а
проміжок інтегрування [0,x]
належить області збіжності цього ряду,
то отримаємо функцію F(x).
Наближене розв’язання степеневих рядів
Розглянемо диф. рівняння y` = f(x,y);
y(x0) = y0 (12.1)
Шукаємо розв’язок 12.1 у вигляді ряду:
y(x)
=
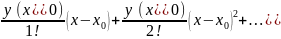
y`(x0) знаходимо з 12.1 підстановкою x0 та y0. Щоб знайти y`` - диференціюємо 12.1 по х.
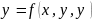
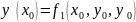
І т.д.
13.Ряди Фур’є. Гармонічні коливання.
Функція
y=f(x)
належить D
має період T>0,
якщо
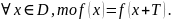
Основні властивості періодичних функцій:
1о. f(x) + F(y) (обидві періодичні) = також функція з періодом T.
2о.
Якщо функція f(x)
має період T,
то f(ax)
має період
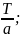
Доказ:
f(a(x+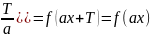
Доказано.
3о.Якщо
f(x)
має період T,
і є інтервал на [x0,x1]
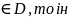 теграл:
теграл:
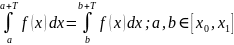
Доказ:
Нехай 0 < a < b < T;
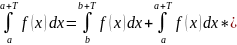

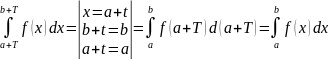
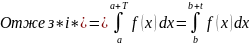
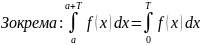
Доказано.
Найпростішими
періодичними коливаннями є прості
гармонічні коливання, що задаються
функцією: y=Asin(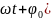 (1.1),
(1.1),
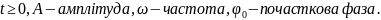
Функцію вигляду 1.1 і її графік називають простою гармонією.
Перетворимо 1.1:
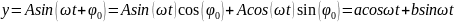
де
b
=
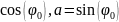 .
.
Основний
період функції 1.1 є T=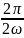 .
.
Зокрема: