Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2327.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

5.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

4.5. Определение элементов взаимного ориентирования

Для определения элементов взаимного ориентирования в качестве исходного используют уравнения взаимного ориентирования

1 bY bZ

Вкачестве примера рассмотримАопределениеДИэлементов взаимного ориентирования by, bz, ω2’, α2’, 2’.

Всвязи с тем, что уравнения (4.24) не линейны, их предварительно приводят к линейному виду и переходят к уравнению поправок:Z′ = 0Y ′X ′б

известным• элементам внутреннего ориентирования снимков fi, x0i, y0i;

• трем параметрам, задающим ориентацию системы координат

Смодели (в нашем случае ω1’, α1’, 1’) и приближенным значениям элементов вза много ор ентирования.

вободный член ℓ выч сляется по формуле (4.25) таким же образом. Полученную систему уравнений поправок решают методом приближений, а в случае, если измерено более пяти точек, – по методу наименьших квадратов (под условием VTPV=min). В результате

решения находят значения элементов взаимного ориентирования. Критерием, по которому принимается решение о завершении

итераций, могут являться величины поправок к определяемым неизвестным или величины остаточных поперечных параллаксов, которые для каждой измеренной точки вычисляются по формуле

106

						f	1	bY	bZ
			q = −			f	X1′	Y1′	Z1′	,	(4.25)
			q = −				X1′	Y1′	Z1′	,	(4.25)
						bZ1′Z2′ X2′		Y2′ Z2′
где b =	1+ by2 + bz2 . Величина q представляет собой разность ординат
измеренных точек на стереопаре снимков, приведенных к идеальному
случаю съемки, т.е. q = y1 – y2.
Необходимо отметить, что при отсутствии ошибок построения
снимка и ошибок измерений величина q должна быть равна 0.
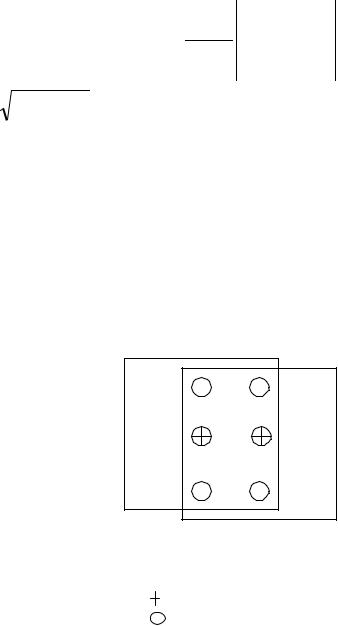
При определении элементов взаимного ориентирования опти-
мальным вариантом считается измерение 12–18 точек на стереопаре
снимков, расположенных парами или тройками в шести стандартных
зонах (рис. 4.3).										И
										И
			Р1					Д
			Р1						Р2
									Р2
				Рис. 4.3			Стандартные
							зоны:
					А
					– главная точка снимка
					– стандартно расположенная зона
		б
В этом случае получается наиболее точное и надежное опреде-
лен е элементов вза много ориентирования и появляется возмож-
ность локал зац			грубых		змерений.
и
		4.6. Построение фотограмметрической модели
Построение фотограмметрической модели заключается в опре-
делении координат точек объекта по измеренным на стереопаре
снимков координатам их изображений в системе координат модели
С
ОМХМYMZM.
							107

Определение координат точек модели производится по формулам (4.4) прямой фотограмметрической засечки (см. раздел 1).

При этом координаты центра проекции S принимаются произвольными (обычно X S1 = YS1 = ZS1 = 0). Также произвольно (но не рав-

ной 0) выбирается величина ВХ. В большинстве случаев практики величину ВХ принимают равной

BX = b m ,

где b – базис фотографирования в масштабе снимка; m – знаменатель масштаба снимка.

Остальные значения элементов внешнего ориентирования опре-

деляют по восьми параметрам by, bz, ω1’, α1’, 1’, ω2’, α2’, 2’, 5 из которых являются элементами взаимного ориентирования, а 3 определяют ориентацию системы координат модели.

При этом

ыли определеныАэлементы взаимного ориентирования by, bz, ω2’, α2’, 2’, а вел ч ны параметров ω1’, α1’, 1’ были приняты

ВY = BX by		ω1 = ω1′	ω2 = ω2′
BZ = BX by		α1 = α1′	И
			α2 = α2′ .
		1 = 1′	2 = ′2
Например, если	определены элементы взаимного ориенти-
		Д
рования α1’, 1’, ω2’, α2’, 2’ при этом величины параметров by, bz,

ω1’ были приняты равными нулю (by=bz=ω1’=0), то BY=BZ=0, ω1=0,

α1=α1’, 1= 1’, ω2=ω2’, α2=α2’, 2= 2’.

равными нулю (ω1’= α1’= 1’=0), то

	BY = BX by	ω1 = 0	ω2 = ω2′
	были		α2 = α2′ .
	BZ = BX bz	α1 = 0	α2 = α2′ .
Если		1 = 0	′
		1 = 0	2 = 2

С

108

4.7. Внешнее ориентирование модели. Элементы внешнего

ориентирования модели

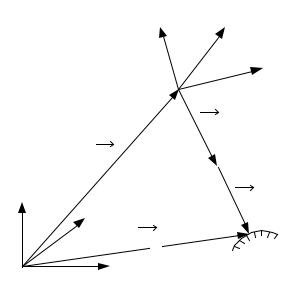
На рис. 4.4:

OXYZ – система координат объекта,

ОМХМYMZM –

система координат фотограмметрической модели , А – точка объекта,

АМ –точка фотограмметрической модели, соответствующая точке А

объекта .

Векторы

и RА определяют положение начала системы коор-

динат модели ОМХМYMZM и точки А местности

относительно начала

системы координат объекта OXYZ.

Из рис. 4.4 следует, что

RA = R0 + R .

(4.27)

Векторы RM и R коллинеарны, поэтому

R = RM t ;

(4.28)

где t – знаменатель масштаба модели.

С учетом (4.28) выражение (4.27) имеет вид:

= R0

+ RM t

(4.29)

•

АR

•

•A

O•

Рис. 4.4

В координатной форме выражение (4.29) имеет вид

+ AM

;

(4.30)

109

или

X = X0 + (a11 X M + a12YM + a13ZM )t

Y = Y

+ (a

+ a Y

+ a

(4.31)

Z = Z

+ (a

+ a Y

+ a

В выражениях (4.30) и (4.31) X, Y, Z – координаты точки объекта

в системе координат объекта; ХМ, YM, ZM – координаты соответствующей точки модели в системе координат фотограмметрической модели; АМ – матрица преобразования координат, элементы aij кото-

Для определения элементов внешнегоДориентирования модели по опорным точкам в качестве исходных используют уравнения

рой являются функциями углов ωМ, αМ, М, определяющих ориентацию системы координат модели относительно системы координат объекта; t – знаменатель масштаба модели.

7 параметров: X0 ,Y0 , Z0 ,ωM ,αM , M ,t – называют элементами
внешнего ориентирования модели.	И

4.8. Определение элементов внешнего ориентирования
модели по опорным точкам

(4.31), которые представим в виде:

X0 + (a11 X M + a12YM + a13ZM )t − X = 0

+ (a

+ a Y

+ a

)t −Y = 0

22 M

+ (a

X А+ a Y + a Z )t − Z = 0

(4.32)

32 M

определенияДля элементов внешнего ориентирования модели необходимо составить систему не менее чем из семи уравнений. Оче-

Каждая планово-высотная опорная точка (X,Y,Z) позволяет со-

став ть 3	уравнен я (4.32), в которых неизвестными являются
7 элементов	внешнего ор ентирования модели. Каждая плановая

Свидно, что для этого необходимо иметь не менее двух планововысотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.

опорная точка (X,Y) позволяет составить два первых уравнения из выражен (4.32), а каждая высотная опорная точка (Z) – третье уравнение из выражения (4.32).

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2813 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20215.54 Mб572322.pdf
#
07.01.20215.54 Mб612323.pdf
#
07.01.20215.59 Mб1402324.pdf
#
07.01.20215.61 Mб682325.pdf
#
07.01.20215.61 Mб312326.pdf
#
07.01.20215.62 Mб742327.pdf
#
07.01.20215.63 Mб572328.pdf
#
07.01.20215.64 Mб432329.pdf
#
07.01.2021362.04 Кб4233.pdf
#
07.01.20215.68 Mб52330.pdf
#
07.01.20215.68 Mб172331.pdf

4.5. Определение элементов взаимного ориентирования

4.6. Построение фотограмметрической модели