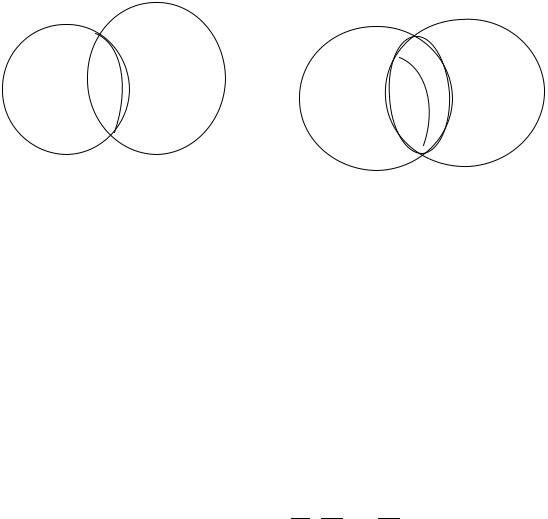
§3. Операции над событиями
Теоремы сложения и умножения вероятностей
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного события: А или В. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий [7].
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
В |
|
Д |
|
|
|
|
|||
|
А |
|
|
|
|
||||||||
|
|
|
|
А |
А |
|
|
А·В |
|
В |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
А+В |
|
и |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Рис. 2.2. Произведение событий |
|||||||||
|
Рис. 2.1. Сумма со ытий |
||||||||||||
|
|
С |
|
|
|
|
|
|
|
|
|||
Пример 1. |
Каждый бз стрелков делает по одному выстрелу в |
||||||||||||
мишень.
а) Какое событие противоположно событию А – “хотя бы один стрелок попал в цель”?
б) Какое событие противоположно событию С – “каждый из стрелков попал в цель”?
Решение.
а) А – “каждый из стрелков промахнулся”. Справедливость ответа вытекает из того, что событие А − означает поражение мишени, а событие А – не поражение мишени;
б) С – “хотя бы один из стрелков промахнулся”.
На основании этого примера приведём формулы, справедливые в алгебре событий: А1 + А2 + ... + Аn = А1 А2 ... Аn ;
66
А1 А2 ... Аn = А1 + А2 + ... + Аn , если Ai обозначает “i -й стрелок попал в цель”, а Ai – “i -й стрелок промахнулся”.
Несовместными событиями называются два события А и В, если не существует элементарного события, благоприятствующего одновременно обоим событиям.
Например, при бросании игральной кости событие А – “выпадает количество очков, равное 1 или 2” и событие В – “выпадает количество очков, равное 4 или 5” не совместны.
Условной вероятностью события А относительно события В называется вероятность события А, вычисленная в предположении, что имело место событие В. Эта вероятность обозначается Р = (А/ В) , или РА (В).
Например, в урне 4 белых и 3 чёрных шара. Из урны последовательно вынимают два шара. Найти вероятность того, что второй шар окажется чёрным при условии, что первый был чёрным.
Обозначим события: В – “первый шар чёрный”; А – “второй – чёрный”. Если произошло событие В, то в урне осталось 6 шаров, из
которых два чёрных. Поэтому искомая условная вероятность |
||||||
Р(А/ В) = 2/ 6 = 1 . |
|
|
А |
И |
|
|
3 |
|
|
|
|
|
|
Вероятность произведения двухДсобытий равна вероятности |
||||||
одного из них, умноженной на условную вероятность другого относи- |
||||||
тельно первого: |
и |
|
|
|
|
|
|
|
|
|
|
|
|
Р(А В) = Р(А) Р(В / А) = Р(В) Р(А / В). |
(2.2) |
|||||
Для нескольк х событбй |
|
|
(2.3) |
|||
Р(А1 А2 ... Аn ) = Р(А1) Р(А2 / А1) ... Р(Аn / А1 ... Аn−1) . |
||||||
События А или В называются независимыми, если |
|
|||||
В этом случаеС |
Р(А В) = Р(А) Р(В) . |
|
||||
|
|
Р(В) = Р(В / А). |
(2.4) |
|||
|
Р( А) = Р( А/ В); |
|||||
Верно и обратное утверждение. |
|
|
||||
События А1, А2 ,..., Аn называются независимыми в совокупности, |
||||||
если |
|
n |
|
n |
|
|
|
|
|
|
(2.5) |
||
|
|
Р(П A ) = |
П Р(А ) . |
|||
|
|
l=1 |
i |
l=1 |
i |
|
Вероятность суммы двух несовместных событий А и В равна |
||||||
сумме вероятностей этих событий: |
|
|
|
|||
|
|
Р(А + В) = Р(А) + Р(В). |
(2.6) |
|||
67
Вероятность суммы нескольких несовместных событий равна сумме их вероятностей:
|
|
|
n |
n |
|
|
|
Р(∑ Ai ) = ∑ P(Ai ). |
(2.7) |
||
|
|
|
l=1 |
l=1 |
|
Если события А и В совместны, вероятность их суммы вычисля- |
|||||
ется по формуле |
|
|
|
|
|
Р(А + В) = Р(А) + Р(В) − Р(А В). |
(2.8) |
||||
Для нескольких совместных событий вероятность их суммы оп- |
|||||
ределяется по формуле |
|
|
|
||
n |
|
|
|
|
|
Р(∑ Ai ) = ∑ P(Ai ) − ∑ P(Ai Aj ) + ∑ P(Ai Aj Ak ) −... + |
|
||||
l=1 |
i |
|
i j |
i j k |
|
+ (−1)n−1 P(A A ... A ), |
|
(2.9) |
|||
|
1 |
2 |
n |
И |
|
где суммы распространяются на все возможные комбинации различ- |
|||||
ных индексов i, |
j, k,..., |
взятых по одному, по два, по три и т. д. |
|
||
|
|
|
|
Д |
|
Задача 1. На заводе в цехе деталь определённого сорта изготов-
ляют на двух станках. Вероятность изготовления детали на первом
станке равна 0,6. Вероятность изготовления годной детали на первом |
||
|
|
А |
станке равна 0,8. Найти вероятность того, что годную деталь изгото- |
||
вили на первом станке. |
б |
|
Решение. Обозначим со ытия: – “деталь изготовлена на пер- |
||
вом станке”, В – “деталь годная”. Имеем Р(А) = 0,6; Р(В / А) = 0,8 . |
||
и |
|
|
По формуле (2.2) наход мР(А В) = Р(А) Р(В / А) = 0,6 0,8 = 0,48. |
||
Задача 2. В ящ ке наход тся 7 деталей первого сорта, 5 – второ- |
||
С |
|
|
го сорта и 3 – третьего сорта. Из ящика последовательно вынимают три детали. Найти вероятность того, что первая, наугад вынутая, деталь окажется первого сорта (событие А1 ), вторая деталь – второго
сорта (событие А2 ) и третья деталь – третьего сорта (событие А3 ).
Решение. |
Очевидно, что |
|
Р(А ) = |
7 |
; |
Р(А |
/ А ) = |
5 |
; |
||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
15 |
|
2 |
1 |
14 |
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
Р(А |
/ А А ) = |
|
, т. к. событие |
А / А означает, что второй раз вы- |
|||||||||||
|
|
||||||||||||||
3 |
1 |
2 |
13 |
2 |
1 |
|
|
|
|
|
|
|
|
||
нули деталь второго сорта при условии, что первый раз была вынута деталь первого сорта. Значит, при повторном вытягивании в ящике осталось 14 деталей, из них второго сорта – 5. Аналогично находим Р(А3 / А1 А2 ) по формуле (2.3).
Р(А1 А2 А3 ) = Р(А1 ) Р(А2 / А1 ) Р(А3 / А1 А2 ) = 157 145 133 = 261 .
68
Задача 3. В ящике имеется 90 стандартных деталей и 10 нестандартных. Из ящика наугад берут одну за другой две детали. “Появление стандартной детали при первом испытании” – событие А, “появление стандартной детали при втором испытании” – событие В. Проверить, зависимы или не зависимы события А и В.
Решение. Р(А) = 10090 = 0,9 . Вероятность события В зависит от
результата первого испытания: если в первом испытании событие А произошло, то
|
Р(В / А) = |
|
90 −1 |
|
= |
89 ; |
||||
|
100 −1 |
|||||||||
|
|
|
|
|
|
99 |
||||
если же событие А не произошло, то |
90 |
|
|
|
10 . |
|||||
|
Р(В / |
|
) = |
|
|
|
= |
|||
|
А |
|
|
|
||||||
|
100 −1 |
|||||||||
События А и В зависимы, т. к. |
|
11 |
||||||||
|
89 = Р(В / А). |
|||||||||
|
Р(А) = 0,9 ≠ |
|||||||||
|
|
|
|
|
|
99 |
|
|
|
|
Задача 4. |
|
А |
|
|
||||||
Найти вероятность того, чтоИпри бросании двух иг- |
||||||||||
ральных костей хотя бы один раз выпадет 6 очков. |
||||||||||
|
б |
|
1 |
|
|
|
1 |
|||
Решение. |
Обозначим события: |
|
Д– “выпадает 6 очков при броса- |
|||||||
нии первой игральной кости”, В – “выпадает 6 очков при бросании |
||||||||||
|
и |
|
|
|
|
события А и В совместны, то |
||||
второй игральной кости”. Так как |
||||||||||
Р(А + В) = Р(А) + Р(В) − Р(А В) . Р(А В) = Р(А) Р(В) , т. к. события
|
|
|
С |
|
Р(А) = 6 |
|
Р(В) = 6 |
|
||||
независимы. |
|
|
Так |
|
|
как |
; |
, поэтому |
||||
Р(А + В) = |
1 |
+ |
1 |
− 1 |
|
1 |
= |
11 . |
|
|
|
|
|
6 |
|
6 |
6 |
|
6 |
|
36 |
|
|
|
|
Задача 5. Электрическая цепь между точками М и N составлена
по схеме (рис. 2.3). Выход из строя элемента a – событие A , элемен- |
||||||||
та bk – событие |
Bk (k = 1, 2, 3) . Записать выражение |
для событий |
||||||
C и |
|
, если С означает разрыв цепи. |
|
|
|
|||
C |
|
|
|
|||||
|
|
|
|
|
b1 |
|
|
|
|
|
М |
|
|
|
b2 |
|
N |
|
|
|
а |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b3 |
|
|
|
|
|
|
|
Рис. 2.3. Схема электрической цепи |
|
|||
69
Решение. Разрыв цепи произойдет в том случае, если выйдет из строя элемент a или все три элемента bk (k =1, 2, 3). Эти события со-
ответственно равны A и B1B2 B3 . Поэтому C = A + B1B2 B3 .
Разрыв цепи не произойдет, если не выйдет из строя элемент a и хотя бы один из элементов bk (k = 1, 2, 3). Эти события соответствен-
но равны A и В1 + В2 + В3 . Следовательно, С = А (В1 + В2 + В3 ).
|
Задачи для самостоятельного решения |
1. |
По мишени производится три выстрела. Рассматриваются со- |
бытия |
Ai – попадание при i -м выстреле (i =1, 2, 3). Представить в |
виде сумм, произведений или сумм произведений событий Ai и Ai следующие события:
А – все три попадания; |
|
|
Д |
|
|
|
|||||||||||
В – все три промаха; |
|
|
|
|
|
И |
|
|
|
||||||||
С – хотя бы одно попадание; |
|
|
|
|
|||||||||||||
Д – хотя бы один промах; |
А |
|
|
|
|||||||||||||
Е – не менее двух попаданий; |
|
|
|
|
|
|
|
||||||||||
F – не больше одного попадания; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|||
G – попадание в мишень не раньше, чем при третьем выстреле. |
|||||||||||||||||
2. Записать событие, состоящее в том, что система исправна |
|||||||||||||||||
|
|
|
|
|
|
и b1 |
|
|
|
|
|
|
|
||||
(дублирующие блоки о означены одинаковыми буквами), система |
|||||||||||||||||
неисправна (рис. 2.4). |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
с |
|
d |
|
|
||||||
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.4. Блок-схема определения неисправности системы
3. Какова вероятность извлечь из колоды в 52 карты фигуру любой масти или карту пиковой масти (фигурой называется валет, дама или король)?
4. В урне 10 белых и 20 черных шаров. Из 10 белых – 6 штрихованных, из 20 черных – 5 штрихованных. Рассматриваются события:
70
А – извлечение из урны белого шара; В – извлечение из урны штрихованного шара.
Определить, зависимы или независимы события А и В.
5. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. При изготовлении такой же детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены две детали, на втором – три. Найти вероятность того, что все детали первосортные.
6. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор срабатывает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только
один сигнализатор. Найти вероятность того, что сработает хотя бы |
|
один сигнализатор. |
И |
|
|
7. Дана система S (рис. 2.5). Блоки, обозначенные одинаковыми |
|
|
Д |
буквами, одинаковы; все блоки независимы. Вычислить надежность системы (вероятность безотказной работы в течение определенного
времени), если известны надежность блоков: P(ai ) = 0,8; P(bi ) = 0,9. |
||||||||
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
б |
|
|
|
|||
|
|
|
|
|
|
|
|
|
и |
|
|
|
а2 |
|
|||
С |
а1 |
|
|
|
|
|||
в1 |
|
|
|
в2 |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5. Блок-схема определения надежности системы
8. На шести карточках написаны буквы к, а, р, е, т, а. После тщательного перемешивания берут наудачу по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «ракета»?
9. Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что вытянутый студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?
71
10. В урне 3 белых и 4 черных шара. Из урны вынимают одн о- временно два шара. Какое событие более вероятно: А – шары одного цвета; В – шары разных цветов?
11. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Ответы
1. A = A1 A2 A3; B = A1 A2 A3;
C = A1 + A2 + A3 , илиC = A1 + A1 A2 + A1 A2 A3 , или
C = A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 ;
Д = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И26 |
|||
A1 + A2 + A3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
E = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A1 A2 A3 + A1 A2 A3 + A1 A2 A3 + A1 A2 A3 = A1 A2 A3 + A1 A2 A3 + A1 A2 ; |
||||||||||||||||||||||||||||||||||||||
F = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G = |
|
|
Д |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
A1 A2 A3 + A1 A2 A3 + A1 A2 ; |
A1 A2 . |
|
|
|
. 3. P = 11 . |
|||||||||||||||||||||||||||||||||
2. S = A(B + B )CД; |
|
= |
|
+ |
|
|
|
+ |
|
+ |
|
|
|
|||||||||||||||||||||||||
S |
A |
B |
B |
C |
|
|
|
|||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
6. а) P = 0,14; б) P = 0,995. |
|||||||||||||
4. А и В – зависимые события. 5. P = |
0,251. |
|
||||||||||||||||||||||||||||||||||||
7. P = 0,92 . 8. P = 0,0028 |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
. 9. |
P = 0,692 . 10. P(B) > P(A). |
|||||||||||||||||||||||||||||||||||||
11. P = 0,0014. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1.Какова Свероятность того, что выбранное наудачу изделие окажется первосортным, если известно, что 3% всей продукции составляют нестандартные изделия, 75% стандартных изделий удовлетворяют требованиям первого сорта?
2.На 20-ти одинаковых жетонах написаны 20 двухзначных чисел от 11 до 30. Жетоны помещают в конверт и тщательно перемешивают. Какова вероятность вынуть жетон с номером, кратным 4 или 7?
3.Вероятности попадания в цель при стрельбе из трёх орудий со-
ответственно равны 0,7;0,8 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.и
72